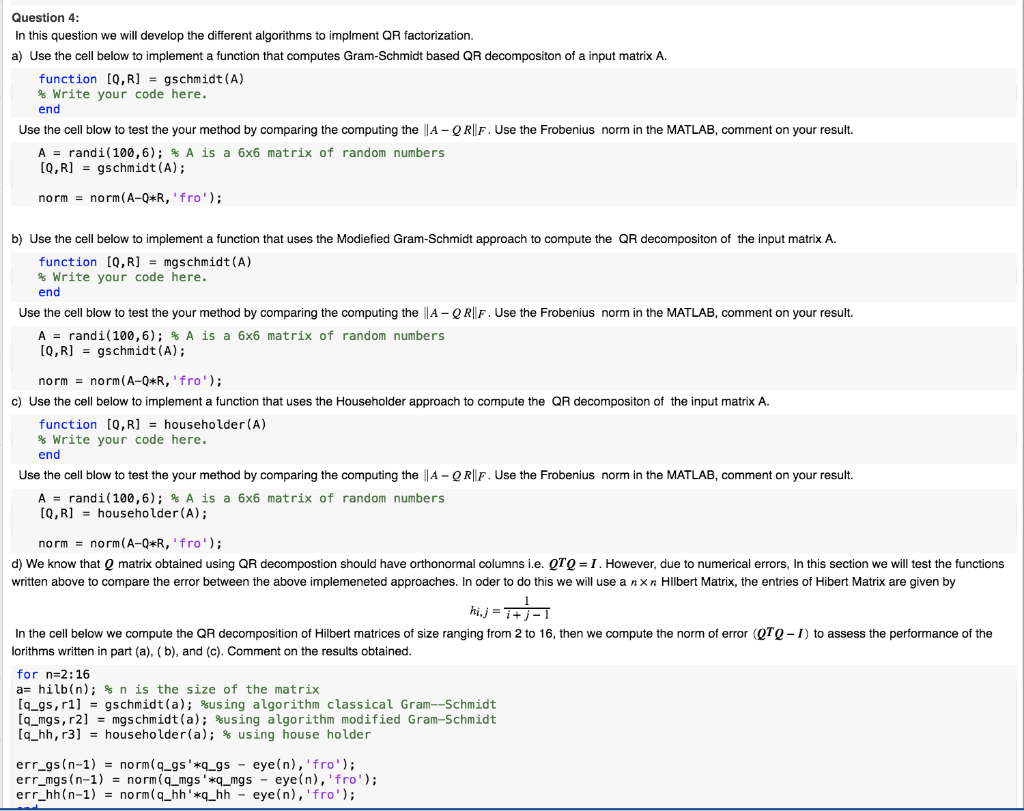
Question 4: In this question we will develop the different algorithms to implment QR factorization. a) Use the cell below to implement a function that computes Gram-Schmidt based QR decompositon of a input matrix A. function [Q,R] = gschmidt (A) % Write your code here. end Use the cell blow to test the your method by comparing the computing the |A - QR||F. Use the Frobenius norm in the MATLAB, comment on your result. A = randi(100,6); % A is a 6x6 matrix of random numbers [0,R] = gschmidt(A); norm = norm(A-Q*R, 'fro'); b) Use the cell below to implement a function that uses the Modiefied Gram-Schmidt approach to compute the QR decompositon of the input matrix A. function (0,R] = mgschmidt (A) % Write your code here. end Use the cell blow to test the your method by comparing the computing the A-QR|F. Use the Frobenius norm in the MATLAB, comment on your result. A = randi(100,6); % A is a 6x6 matrix of random numbers [Q,R] = gschmidt(A); norm = norm(A-Q*R, 'fro'); c) Use the cell below to implement a function that uses the Householder approach to compute the QR decompositon of the input matrix A. function (0,R] = householder(A) % Write your code here. end Use the cell blow to test the your method by comparing the computing the |A - ORF. Use the Frobenius norm in the MATLAB, comment on your result. A = randi(100,6); % A is a 6x6 matrix of random numbers [Q,R] = householder(A); norm = norm(A-Q*R, 'fro'); d) We know that Q matrix obtained using QR decompostion should have orthonormal columns i.e. QTQ = 1. However, due to numerical errors, In this section we will test the functions written above to compare the error between the above implemeneted approaches. In oder to do this we will use a nxn Hilbert Matrix, the entries of Hibert Matrix are given by = In the cell below we compute the QR decomposition of Hilbert matrices of size ranging from 2 to 16, then we compute the norm of error (QTQ-I) to assess the performance of the lorithms written in part (a), (b), and (c). Comment on the results obtained. for n=2:16 a= hilb(n); % n is the size of the matrix [q_gs, r1] = gschmidt(a); $using algorithm classical Gram--Schmidt [q_mgs, r2] = mgschmidt(a); using algorithm modified Gram-Schmidt [q_hh, r3] = householder(a); % using house holder err_gs(n-1) = norm(q_gs'*q_9s - eye(n), 'fro'); err_mgs(n-1) = norm(q_mgs '*q_mgs eye(n), 'fro'); err_hh(n-1) = norm(q_hh'*q_hh - eye(n),'fro'); figure(4) hold on grid on plot(err_gs,'b-d') plot(err_mgs,'r-o') plot(err_hh, 'g-s') ylabel('Frobenius Norm of error matrix'); xlabel('Matrix Size [n]') legend('classical Gram-Schmidt', 'Modified Gram-Schmidt', 'Householder'); e) Finally, now we have implemented various different versions of QR decompositon. Use above versions of the the QR transform and use this to fit the polynomial in question 3. We want to fit the polynomial of degree 14 through the data with 15 points. Clearly show all the plots (with legends) and comment on the results obtained. % Implement Question 4 part e here. Use the code privided in Question 3 part (d) for inspitration. Appendix 1 function A = Hilbert_matrix(size) A = zeros(size, size); for i=1: size for j=1: size Ali,j) = 1/(i+j-1); end end Question 4: In this question we will develop the different algorithms to implment QR factorization. a) Use the cell below to implement a function that computes Gram-Schmidt based QR decompositon of a input matrix A. function [Q,R] = gschmidt (A) % Write your code here. end Use the cell blow to test the your method by comparing the computing the |A - QR||F. Use the Frobenius norm in the MATLAB, comment on your result. A = randi(100,6); % A is a 6x6 matrix of random numbers [0,R] = gschmidt(A); norm = norm(A-Q*R, 'fro'); b) Use the cell below to implement a function that uses the Modiefied Gram-Schmidt approach to compute the QR decompositon of the input matrix A. function (0,R] = mgschmidt (A) % Write your code here. end Use the cell blow to test the your method by comparing the computing the A-QR|F. Use the Frobenius norm in the MATLAB, comment on your result. A = randi(100,6); % A is a 6x6 matrix of random numbers [Q,R] = gschmidt(A); norm = norm(A-Q*R, 'fro'); c) Use the cell below to implement a function that uses the Householder approach to compute the QR decompositon of the input matrix A. function (0,R] = householder(A) % Write your code here. end Use the cell blow to test the your method by comparing the computing the |A - ORF. Use the Frobenius norm in the MATLAB, comment on your result. A = randi(100,6); % A is a 6x6 matrix of random numbers [Q,R] = householder(A); norm = norm(A-Q*R, 'fro'); d) We know that Q matrix obtained using QR decompostion should have orthonormal columns i.e. QTQ = 1. However, due to numerical errors, In this section we will test the functions written above to compare the error between the above implemeneted approaches. In oder to do this we will use a nxn Hilbert Matrix, the entries of Hibert Matrix are given by = In the cell below we compute the QR decomposition of Hilbert matrices of size ranging from 2 to 16, then we compute the norm of error (QTQ-I) to assess the performance of the lorithms written in part (a), (b), and (c). Comment on the results obtained. for n=2:16 a= hilb(n); % n is the size of the matrix [q_gs, r1] = gschmidt(a); $using algorithm classical Gram--Schmidt [q_mgs, r2] = mgschmidt(a); using algorithm modified Gram-Schmidt [q_hh, r3] = householder(a); % using house holder err_gs(n-1) = norm(q_gs'*q_9s - eye(n), 'fro'); err_mgs(n-1) = norm(q_mgs '*q_mgs eye(n), 'fro'); err_hh(n-1) = norm(q_hh'*q_hh - eye(n),'fro'); figure(4) hold on grid on plot(err_gs,'b-d') plot(err_mgs,'r-o') plot(err_hh, 'g-s') ylabel('Frobenius Norm of error matrix'); xlabel('Matrix Size [n]') legend('classical Gram-Schmidt', 'Modified Gram-Schmidt', 'Householder'); e) Finally, now we have implemented various different versions of QR decompositon. Use above versions of the the QR transform and use this to fit the polynomial in question 3. We want to fit the polynomial of degree 14 through the data with 15 points. Clearly show all the plots (with legends) and comment on the results obtained. % Implement Question 4 part e here. Use the code privided in Question 3 part (d) for inspitration. Appendix 1 function A = Hilbert_matrix(size) A = zeros(size, size); for i=1: size for j=1: size Ali,j) = 1/(i+j-1); end end