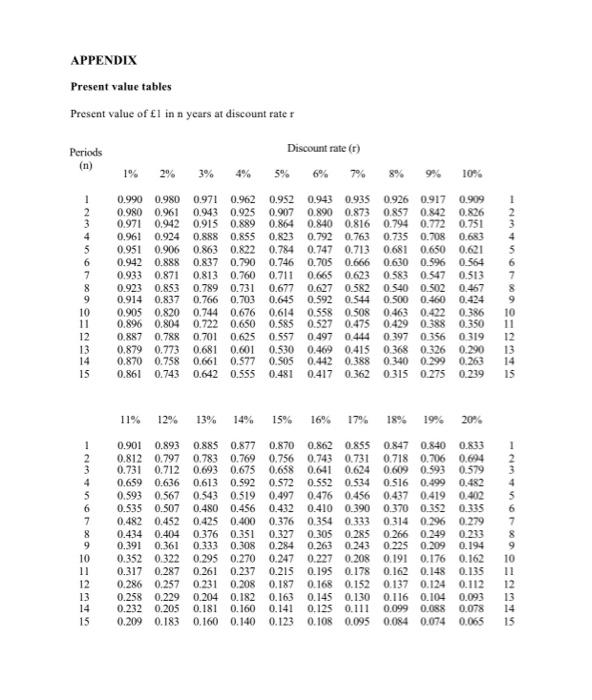
Question 4 You should assume that the current date is 31 December 2020 Lewis plc (Lewis) is a UK-based manufacturer of industrial goods. Lewis sources its components and raw materials from European suppliers and pays for these in euros. You work in Lewis's finance department and have been asked to provide guidance on two issues to be discussed at the next board meeting, Issue 1 - Jorex contract Lewis recently signed a contract for the supply of components with a new French supplier, Jorex. The first consignment of components is due to be received on 31 January 2021 and payment of 1,650,000 will be made to Jorex two months later. Lewis's board have asked for details of how the foreign exchange rate risk on this payment might be hedged. Four possible strategies are under consideration by the board: Do not hedge Use a forward contract Use a money market hedge Use an over-the-counter (OTC) option You have the following data available at the close of business on 31 December 2020: Spot rate (C/) 1.1650 - 1.1740 3-month forward contract (C/) 1.1602 - 1.1708 Forward contract arrangement fee 3,500 3-month OTC put option on - exercise price 1.1650/ 3-month OTC call option on - exercise price 1.1539/ Cost of relevant OTC option 0.60 per 100 converted Sterling interest rate (depositing) 4.1% pa Sterling interest rate (borrowing) 4.5% pa Euro interest rate (depositing) 2.1% pa Euro interest rate (borrowing) 3.3% pa Issue 2 - interest rate hedging Lewis recently bought new premises and borrowed 75 million for a period of twelve years. The loan is at a floating rate of LIBOR + 3% pa. LIBOR is currently 0.5% pa. The finance director of Lewis believes that interest rates are going to rise and she would like to protect the company against interest rate risk. The finance director of Lewis identified Dill plc (Dill), which is a company that would like to swap 75 million of its 4% pa fixed rate loans to a floating rate. Lewis and Dill agreed to enter into an interest rate swap with any benefits from the swap being shared in the ratio 50:50 between the two companies. Lewis can borrow at a fixed rate of 5.5% pa and Dill can borrow at a floating rate of LIBOR + 2.5% pa. Question 4 continued Requirements (a) For issue 1, calculate Lewis's sterling payment for the four possible strategies under consideration assuming that on 31 March 2021 the relevant spot exchange rate will be: either 1.0865 / or 1.1735/ (13 marks) (b) Using your results from (a) above, advise Lewis's board whether it should hedge against movements in the value of the euro. (7 marks) (c) For issue 2, demonstrate how the interest rate swap between Lewis and Dill would be implemented, with the floating rate leg of the swap set at LIBOR. (5 marks) (Total 25 marks) APPENDIX Present value tables Present value of 1 in n years at discount rater Periods Discount rate (r) (n) 1% 2% % 7% 8% 9 10% 1 2 3 1 2 3 4 5 6 7 8 9 10 0.990 0.980 0.971 0.962 0.952 0.943 0.935 0.926 0.917 0.909 0.980 0.961 0.943 0.925 0.907 0.890 0.873 0.857 0.842 0.826 0.971 0.942 0,915 0.889 0.864 0.840 0.816 0.794 0.772 0.751 0.961 0.924 0.888 0.855 0.823 0.792 0.763 0.735 0.708 0.683 0.951 0.906 0.863 0.822 0.784 0.747 0.713 0.681 0.650 0.621 0.942 0.888 0.837 0.790 0.746 0.705 0.666 0.630 0.596 0.564 0.933 0.871 0.813 0.760 0.711 0.665 0.623 0.583 0.547 0.513 0.923 0.853 0.789 0.731 0.677 0.627 0.582 0.540 0.502 0.467 0.914 0.837 0.766 0.703 0.645 0.592 0.544 0.500 0.460 0.424 0.905 0.820 0.744 0.676 0.614 0.558 0.508 0.463 0.422 0.386 0.896 0.804 0.722 0.650 0.585 0.527 0.475 0.429 0.388 0.350 0.887 0.788 0.701 0.625 0.557 0.497 0.444 0.397 0.356 0319 0.879 0.773 0.681 0.601 0.530 0.469 0.415 0.368 0.326 0.290 0.870 0.758 0.661 0.577 0.505 0.442 0.388 0.340 0.299 0.263 0.861 0.743 0.642 0.555 0.481 0.417 0.362 0.315 0.275 0.239 5 6 7 8 9 10 12 13 14 15 12 13 14 15 11% 12% 13% 15% 16% 17% 18% 19% 20% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0.901 0.893 0.885 0.877 0.870 0.862 0.855 0.847 0.840 0.833 0.812 0.797 0.783 0.769 0.756 0.743 0.731 0.7180.706 0.694 0.731 0.712 0.693 0.675 0.658 0.641 0.624 0.609 0.593 0.579 0.659 0.636 0.613 0.592 0.572 0.552 0.534 0.516 0.499 0.482 0.593 0.567 0.543 0.519 0.497 0.476 0.456 0.437 0.419 0.402 0.535 0.507 0.480 0.456 0.432 0.410 0.390 0.370 0352 0.335 0.482 0.452 0.425 0.400 0.376 0.354 0.333 0.314 0.296 0.279 0.434 0.404 0.376 0.351 0.327 0.305 0.285 0.266 0.249 0.233 0.391 0.361 0.333 0.308 0.284 0.263 0.243 0.225 0.209 0.194 0.352 0.322 0.295 0.270 0.247 0.227 0.208 0.191 0.176 0.162 0.317 0.287 0.261 0.237 0.215 0.195 0.178 0.162 0.148 0.135 0.286 0.257 0.231 0.208 0.187 0.168 0.152 0.137 0.124 0.112 0.258 0.229 0.204 0.182 0.163 0.145 0.130 0.116 0.104 0.093 0.232 0.205 0.181 0.160 0.141 0.125 0.111 0.099 0.088 0.078 0.209 0.183 0.160 0.140 0.123 0.108 0.095 0.084 0.074 0.065 4 5 6 7 8 9 10 11 12 13 14 15 Annuity tables Present value of l receivable at the end of each year for n years at discount rater Periods Discount rate (1) 1% 2% 3% 4% 5% 7% 8% 9% 10% 1 2 3 4 5 6 7 8 9 10 11 12 13 0.990 0.980 0.971 0.962 0.952 0.943 0.935 0.926 0.917 1.970 1.942 1.913 1.886 1.859 1.833 1.808 1.783 1.759 2.941 2.884 2.829 2.775 2.723 2.673 2.624 2.577 2.531 3.902 3.808 3.717 3.630 3.546 3.465 3.387 3.312 3.240 4.853 4.713 4.580 4.452 4.329 4.212 4.100 3.993 3.890 5.795 5.601 5.417 5.242 5.076 4.917 4.767 4.623 4.486 6.728 6.472 6.230 6.002 5.786 5.582 5.389 5.206 5.033 7.652 7.325 7.020 6.733 6.463 6.210 5.971 5.747 5.535 8.566 8.162 7.786 7.435 7.108 6.802 6.515 6.247 5.995 9.471 8.983 8.530 8.111 7.722 7.360 7.024 6.710 6.418 10.368 9.787 9.253 8.760 8.306 7.887 7.499 7.139 6.805 11.255 10.575 9.954 9.385 8.863 8.384 7.943 7.536 7.161 12.134 11.348 10.635 9.986 9.394 8.853 8.358 7.904 7.487 13.004 12.106 11.296 10.563 9.899 9.295 8.745 8.244 7.786 13.865 12.849 11.938 11.118 10.380 9.712 9.108 8.559 8.061 0.909 1.736 2.487 3.170 3.791 4.355 4.868 5.335 5.759 6.145 6.495 6,814 7.103 7.367 7.606 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 15 11% 12% 13% 14% 15% 16% 17% 18% 19% 20% 1 2 3 4 6 7 8 9 10 11 12 13 14 0.901 0.893 1.713 1.690 2.444 2.402 3.102 3.037 3.696 3.605 4.231 4.111 4.712 4.564 5.146 4.968 5.537 5.328 5.889 5.650 6.207 5.938 6.492 6.194 6.750 6.424 6.982 6.618 7.191 6.811 0.885 0.877 1.668 1.647 2.361 2.322 2.974 2.914 3.517 3.433 3.998 3.889 4.423 4.288 4.799 4.639 5.132 4.946 5.426 5.216 5.687 5.453 5.918 5.660 6.122 5.842 6.302 6.002 6.462 6.142 0.870 1.626 2.283 2.855 3.352 3.784 4.160 4.487 4.772 5.019 5.234 5.421 5.583 5.724 5.847 0.862 0.855 0.847 0.840 1.605 1.585 1.566 1.547 2.246 2.210 2.174 2.140 2.798 2.743 2.690 2.639 3.274 3.199 3.127 3.058 3.685 3.589 3.498 3.410 4.039 3.922 3.812 3.706 4.344 4.207 4.078 3.954 4.607 4.451 4.303 4.163 4.833 4.659 4.494 4.339 5.029 4.836 4.656 4.486 5.197 4.988 4.793 4.611 5.342 5.118 4.910 4.715 5.468 5.229 5.008 4.802 5.575 5.324 5.092 4.876 0.833 1.528 2.106 2.589 2.991 3.326 3.605 3.837 4.031 4.192 4.327 4.439 4.533 4.611 4.675 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Formulae sheet 1. Expected retum xp Ix outcome, p = probability of outcome) 1 2. Variance of 3. Standard deviation of 4. Expected retur on a 2 asset portfolio i, ai, ai, [a= proportion of funds invested in A whose mean retumis ij 5. Risk (standard deviation) of a 2 asset portfolio , vao (1-a) o 23(1-2)covit..ta) 6. Covariance coven) (MP [ta= outcomes for Aj CO2 7. Correlation con 8. CAPM required rate of return = r, B,(r. 1) In = risk free rate, tm = retum an market portfolio. B = beta of investment cov,) com 10 = standard deviation of j's retums 10. Beta of a firm with various activities B x, where x is the weighting for each activity D 11. Dividend valuation model generally P, IP = share price at time of D 12. DVM with constant growth P. D.01 ) D.(1 ) P & D P D. = current dividend D. = dividend in ne year 9- growth in dividends k = cost of equity] = interest on face value. T=tax] 13. After tax cost of irredeemable debtk (1 T) P 14. After tax cost of redeemable debt solve 0 (P) (I-TXAF. RV (I k.) where AF is an annuity factor and RV is the redemption value NPV NPV, NPV) Irdiscount rate giving NPV) UMADFR-15-3 Page 11 of 13 15. IRR Question 4 You should assume that the current date is 31 December 2020 Lewis plc (Lewis) is a UK-based manufacturer of industrial goods. Lewis sources its components and raw materials from European suppliers and pays for these in euros. You work in Lewis's finance department and have been asked to provide guidance on two issues to be discussed at the next board meeting, Issue 1 - Jorex contract Lewis recently signed a contract for the supply of components with a new French supplier, Jorex. The first consignment of components is due to be received on 31 January 2021 and payment of 1,650,000 will be made to Jorex two months later. Lewis's board have asked for details of how the foreign exchange rate risk on this payment might be hedged. Four possible strategies are under consideration by the board: Do not hedge Use a forward contract Use a money market hedge Use an over-the-counter (OTC) option You have the following data available at the close of business on 31 December 2020: Spot rate (C/) 1.1650 - 1.1740 3-month forward contract (C/) 1.1602 - 1.1708 Forward contract arrangement fee 3,500 3-month OTC put option on - exercise price 1.1650/ 3-month OTC call option on - exercise price 1.1539/ Cost of relevant OTC option 0.60 per 100 converted Sterling interest rate (depositing) 4.1% pa Sterling interest rate (borrowing) 4.5% pa Euro interest rate (depositing) 2.1% pa Euro interest rate (borrowing) 3.3% pa Issue 2 - interest rate hedging Lewis recently bought new premises and borrowed 75 million for a period of twelve years. The loan is at a floating rate of LIBOR + 3% pa. LIBOR is currently 0.5% pa. The finance director of Lewis believes that interest rates are going to rise and she would like to protect the company against interest rate risk. The finance director of Lewis identified Dill plc (Dill), which is a company that would like to swap 75 million of its 4% pa fixed rate loans to a floating rate. Lewis and Dill agreed to enter into an interest rate swap with any benefits from the swap being shared in the ratio 50:50 between the two companies. Lewis can borrow at a fixed rate of 5.5% pa and Dill can borrow at a floating rate of LIBOR + 2.5% pa. Question 4 continued Requirements (a) For issue 1, calculate Lewis's sterling payment for the four possible strategies under consideration assuming that on 31 March 2021 the relevant spot exchange rate will be: either 1.0865 / or 1.1735/ (13 marks) (b) Using your results from (a) above, advise Lewis's board whether it should hedge against movements in the value of the euro. (7 marks) (c) For issue 2, demonstrate how the interest rate swap between Lewis and Dill would be implemented, with the floating rate leg of the swap set at LIBOR. (5 marks) (Total 25 marks) APPENDIX Present value tables Present value of 1 in n years at discount rater Periods Discount rate (r) (n) 1% 2% % 7% 8% 9 10% 1 2 3 1 2 3 4 5 6 7 8 9 10 0.990 0.980 0.971 0.962 0.952 0.943 0.935 0.926 0.917 0.909 0.980 0.961 0.943 0.925 0.907 0.890 0.873 0.857 0.842 0.826 0.971 0.942 0,915 0.889 0.864 0.840 0.816 0.794 0.772 0.751 0.961 0.924 0.888 0.855 0.823 0.792 0.763 0.735 0.708 0.683 0.951 0.906 0.863 0.822 0.784 0.747 0.713 0.681 0.650 0.621 0.942 0.888 0.837 0.790 0.746 0.705 0.666 0.630 0.596 0.564 0.933 0.871 0.813 0.760 0.711 0.665 0.623 0.583 0.547 0.513 0.923 0.853 0.789 0.731 0.677 0.627 0.582 0.540 0.502 0.467 0.914 0.837 0.766 0.703 0.645 0.592 0.544 0.500 0.460 0.424 0.905 0.820 0.744 0.676 0.614 0.558 0.508 0.463 0.422 0.386 0.896 0.804 0.722 0.650 0.585 0.527 0.475 0.429 0.388 0.350 0.887 0.788 0.701 0.625 0.557 0.497 0.444 0.397 0.356 0319 0.879 0.773 0.681 0.601 0.530 0.469 0.415 0.368 0.326 0.290 0.870 0.758 0.661 0.577 0.505 0.442 0.388 0.340 0.299 0.263 0.861 0.743 0.642 0.555 0.481 0.417 0.362 0.315 0.275 0.239 5 6 7 8 9 10 12 13 14 15 12 13 14 15 11% 12% 13% 15% 16% 17% 18% 19% 20% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0.901 0.893 0.885 0.877 0.870 0.862 0.855 0.847 0.840 0.833 0.812 0.797 0.783 0.769 0.756 0.743 0.731 0.7180.706 0.694 0.731 0.712 0.693 0.675 0.658 0.641 0.624 0.609 0.593 0.579 0.659 0.636 0.613 0.592 0.572 0.552 0.534 0.516 0.499 0.482 0.593 0.567 0.543 0.519 0.497 0.476 0.456 0.437 0.419 0.402 0.535 0.507 0.480 0.456 0.432 0.410 0.390 0.370 0352 0.335 0.482 0.452 0.425 0.400 0.376 0.354 0.333 0.314 0.296 0.279 0.434 0.404 0.376 0.351 0.327 0.305 0.285 0.266 0.249 0.233 0.391 0.361 0.333 0.308 0.284 0.263 0.243 0.225 0.209 0.194 0.352 0.322 0.295 0.270 0.247 0.227 0.208 0.191 0.176 0.162 0.317 0.287 0.261 0.237 0.215 0.195 0.178 0.162 0.148 0.135 0.286 0.257 0.231 0.208 0.187 0.168 0.152 0.137 0.124 0.112 0.258 0.229 0.204 0.182 0.163 0.145 0.130 0.116 0.104 0.093 0.232 0.205 0.181 0.160 0.141 0.125 0.111 0.099 0.088 0.078 0.209 0.183 0.160 0.140 0.123 0.108 0.095 0.084 0.074 0.065 4 5 6 7 8 9 10 11 12 13 14 15 Annuity tables Present value of l receivable at the end of each year for n years at discount rater Periods Discount rate (1) 1% 2% 3% 4% 5% 7% 8% 9% 10% 1 2 3 4 5 6 7 8 9 10 11 12 13 0.990 0.980 0.971 0.962 0.952 0.943 0.935 0.926 0.917 1.970 1.942 1.913 1.886 1.859 1.833 1.808 1.783 1.759 2.941 2.884 2.829 2.775 2.723 2.673 2.624 2.577 2.531 3.902 3.808 3.717 3.630 3.546 3.465 3.387 3.312 3.240 4.853 4.713 4.580 4.452 4.329 4.212 4.100 3.993 3.890 5.795 5.601 5.417 5.242 5.076 4.917 4.767 4.623 4.486 6.728 6.472 6.230 6.002 5.786 5.582 5.389 5.206 5.033 7.652 7.325 7.020 6.733 6.463 6.210 5.971 5.747 5.535 8.566 8.162 7.786 7.435 7.108 6.802 6.515 6.247 5.995 9.471 8.983 8.530 8.111 7.722 7.360 7.024 6.710 6.418 10.368 9.787 9.253 8.760 8.306 7.887 7.499 7.139 6.805 11.255 10.575 9.954 9.385 8.863 8.384 7.943 7.536 7.161 12.134 11.348 10.635 9.986 9.394 8.853 8.358 7.904 7.487 13.004 12.106 11.296 10.563 9.899 9.295 8.745 8.244 7.786 13.865 12.849 11.938 11.118 10.380 9.712 9.108 8.559 8.061 0.909 1.736 2.487 3.170 3.791 4.355 4.868 5.335 5.759 6.145 6.495 6,814 7.103 7.367 7.606 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 15 11% 12% 13% 14% 15% 16% 17% 18% 19% 20% 1 2 3 4 6 7 8 9 10 11 12 13 14 0.901 0.893 1.713 1.690 2.444 2.402 3.102 3.037 3.696 3.605 4.231 4.111 4.712 4.564 5.146 4.968 5.537 5.328 5.889 5.650 6.207 5.938 6.492 6.194 6.750 6.424 6.982 6.618 7.191 6.811 0.885 0.877 1.668 1.647 2.361 2.322 2.974 2.914 3.517 3.433 3.998 3.889 4.423 4.288 4.799 4.639 5.132 4.946 5.426 5.216 5.687 5.453 5.918 5.660 6.122 5.842 6.302 6.002 6.462 6.142 0.870 1.626 2.283 2.855 3.352 3.784 4.160 4.487 4.772 5.019 5.234 5.421 5.583 5.724 5.847 0.862 0.855 0.847 0.840 1.605 1.585 1.566 1.547 2.246 2.210 2.174 2.140 2.798 2.743 2.690 2.639 3.274 3.199 3.127 3.058 3.685 3.589 3.498 3.410 4.039 3.922 3.812 3.706 4.344 4.207 4.078 3.954 4.607 4.451 4.303 4.163 4.833 4.659 4.494 4.339 5.029 4.836 4.656 4.486 5.197 4.988 4.793 4.611 5.342 5.118 4.910 4.715 5.468 5.229 5.008 4.802 5.575 5.324 5.092 4.876 0.833 1.528 2.106 2.589 2.991 3.326 3.605 3.837 4.031 4.192 4.327 4.439 4.533 4.611 4.675 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Formulae sheet 1. Expected retum xp Ix outcome, p = probability of outcome) 1 2. Variance of 3. Standard deviation of 4. Expected retur on a 2 asset portfolio i, ai, ai, [a= proportion of funds invested in A whose mean retumis ij 5. Risk (standard deviation) of a 2 asset portfolio , vao (1-a) o 23(1-2)covit..ta) 6. Covariance coven) (MP [ta= outcomes for Aj CO2 7. Correlation con 8. CAPM required rate of return = r, B,(r. 1) In = risk free rate, tm = retum an market portfolio. B = beta of investment cov,) com 10 = standard deviation of j's retums 10. Beta of a firm with various activities B x, where x is the weighting for each activity D 11. Dividend valuation model generally P, IP = share price at time of D 12. DVM with constant growth P. D.01 ) D.(1 ) P & D P D. = current dividend D. = dividend in ne year 9- growth in dividends k = cost of equity] = interest on face value. T=tax] 13. After tax cost of irredeemable debtk (1 T) P 14. After tax cost of redeemable debt solve 0 (P) (I-TXAF. RV (I k.) where AF is an annuity factor and RV is the redemption value NPV NPV, NPV) Irdiscount rate giving NPV) UMADFR-15-3 Page 11 of 13 15. IRR