..Question 5 sample
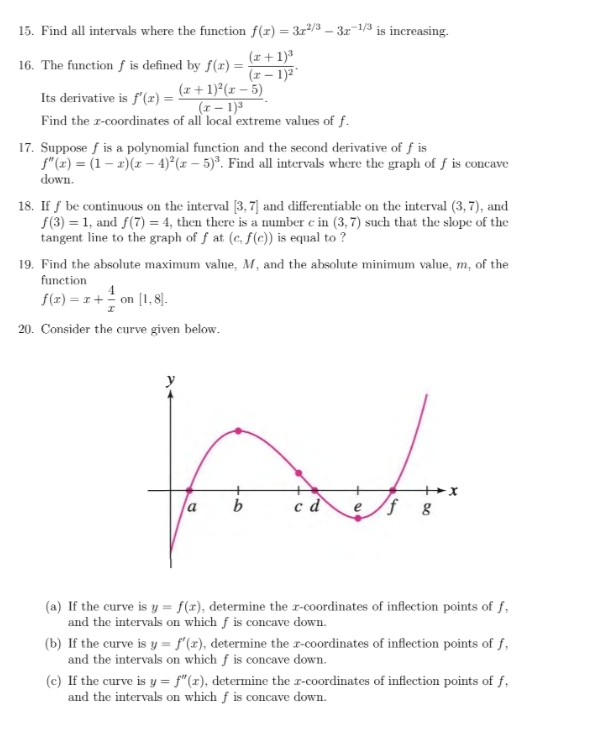
1. Find the linearization, L(x), of the function f(x) = cos(2x) at a = =. 2. Find all critical points of the function f(x) = Vx - 3x - 10. 3. Find all intervals where the function /(x) = 2" - 1523 + 10 is increasing. 4. The function f is defined by /(@) =- x - 2 Find the x-coordinates of all local extreme values of f. 5. The function f is continuous everywhere and f"(x) = (x - 1)*(3 -x)(x + 1)3. Find all intervals where the graph of f is concave down. 6. Find the absolute maximum value, M, and the absolute minimum value, m, of the function f(x) = x+ = on [1, 1). 7. Let f be continuous on the interval [3, 5] and differentiable on the interval (3,5), and f(3) = -1, and f(5) = 1. Which of the following theorems implies that the graph of f has a tangent line with a slope , on the interval (3,5)? (a) The Intermediate Value Theorem (b) The Extreme Value Theorem (c) The Mean Value Theorem (d) Rolle's Theorem (e) No theorem guarantees this because the statement is false. 8. Find all critical numbers of the function /(a) = a - 5x/. Classify whether each correspond to a local minimum, local maximum, or neither. 9. Give an example of a function f such that f(5) is a local maximum and f"(5) = 0. 10. Give an example of a function f such that f"(2) is undefined but f(2) is a local minimum. 11. Give an example of a function f such that f"(3) = 0 but f is concave up for all a. 12. Give an example of a function f such that f(3) is undefined, but f(3) is neither a local minimum nor local maximum. 13. Find the linearization, L(x), of the function f(x) = var + 1 at a = 1. 14. Find all critical points of the function f(x) = z(1 - z)l.15. Find all intervals where the function f(x) = 3p/3 - 3x-1/3 is increasing. 16. The function f is defined by f(2) = (2 + 1)3 (x - 1)2 Its derivative is f'(x) = (3+1)(x-5) (x - 1)3 Find the z-coordinates of all local extreme values of f. 17. Suppose f is a polynomial function and the second derivative of f is "(x) = (1 -x)(x - 4)'(x - 5) . Find all intervals where the graph of f is concave down. 18. If f be continuous on the interval [3, 7] and differentiable on the interval (3, 7), and f(3) = 1, and f(7) = 4, then there is a number c in (3, 7) such that the slope of the tangent line to the graph of f at (c, f(c)) is equal to ? 19. Find the absolute maximum value, M, and the absolute minimum value, m, of the function f(x) = x+ = on [1, 8]. 20. Consider the curve given below. # X a g (a) If the curve is y = f(x), determine the r-coordinates of inflection points of f, and the intervals on which f is concave down. (b) If the curve is y = f'(x), determine the r-coordinates of inflection points of f, and the intervals on which f is concave down. (c) If the curve is y = f"(r), determine the r-coordinates of inflection points of f. and the intervals on which f is concave down