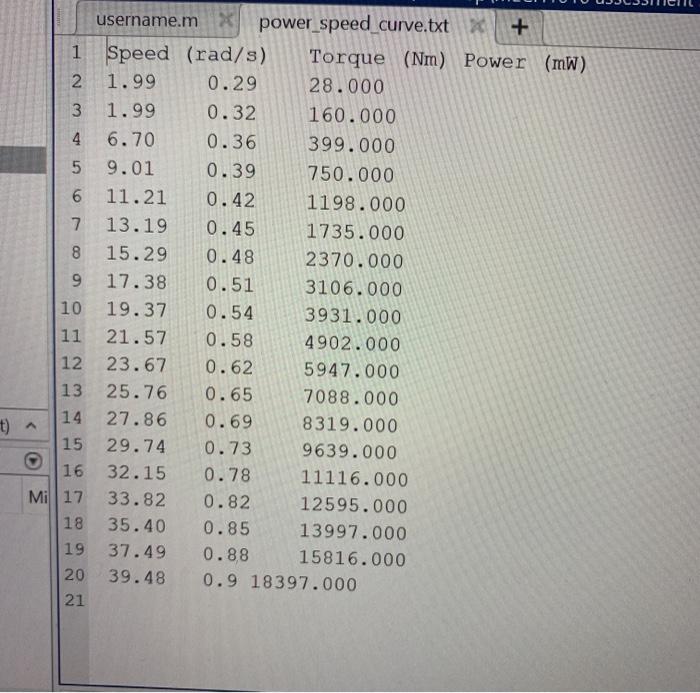
% Question 6 - Basic curve-fitting, symbolic math and plotting. [16 Marks) % Question 6.1 - The file power_speed_curve.txt contains the speed, torque # and power data for the DC generator from the question above. It contains 3 columns of data, the first is the generator speed in rad/3, the second % is the required torque of the generator at each corresponding speed in Nm and the third is the power in milliwatts. The delimiter for the file is a tab. # Read in the data in columns 1 and 3 and set to variables speed_rad and $ power_generated respectively. Convert the speed_rad vector to rpm assigning to a variable speed_rpm. [2 marks] #speed_rad ${power_generated speed_rpm $ Question 6.2 The relationship between speed and power is a second order % polynomial. Use the polyfit function to determine the relationship such % that power generated = atspeed_rpm2 + b*speed_rpm + c. Assign the % calculated coefficients to a vector variable coeffs. [2 marks] %&coeffs 2 3 4 5 8 ON username.m X power_speed curve.txt x + 1 Speed (rad/s) Torque (Nm) Power (mW) 2 1.99 0.29 28.000 3 1.99 0.32 160.000 4 6.70 0.36 399.000 5 9.01 0.39 750.000 6 11.21 0.42 1198.000 7 13.19 0.45 1735.000 8 15.29 0.48 2370.000 9 17.38 0.51 3106.000 10 19.37 0.54 3931.000 11 21.57 0.58 4902.000 12 23.67 0.62 5947.000 13 25.76 0.65 7088.000 14 27.86 0.69 8319.000 15 29.74 0.73 9639.000 16 32.15 0.78 11116.000 Mi 17 33.82 0.82 12595.000 18 35.40 0.85 13997.000 19 37.49 0.88 15816.000 20 39.48 0.9 18397.000 21 % Question 6 - Basic curve-fitting, symbolic math and plotting. [16 Marks) % Question 6.1 - The file power_speed_curve.txt contains the speed, torque # and power data for the DC generator from the question above. It contains 3 columns of data, the first is the generator speed in rad/3, the second % is the required torque of the generator at each corresponding speed in Nm and the third is the power in milliwatts. The delimiter for the file is a tab. # Read in the data in columns 1 and 3 and set to variables speed_rad and $ power_generated respectively. Convert the speed_rad vector to rpm assigning to a variable speed_rpm. [2 marks] #speed_rad ${power_generated speed_rpm $ Question 6.2 The relationship between speed and power is a second order % polynomial. Use the polyfit function to determine the relationship such % that power generated = atspeed_rpm2 + b*speed_rpm + c. Assign the % calculated coefficients to a vector variable coeffs. [2 marks] %&coeffs 2 3 4 5 8 ON username.m X power_speed curve.txt x + 1 Speed (rad/s) Torque (Nm) Power (mW) 2 1.99 0.29 28.000 3 1.99 0.32 160.000 4 6.70 0.36 399.000 5 9.01 0.39 750.000 6 11.21 0.42 1198.000 7 13.19 0.45 1735.000 8 15.29 0.48 2370.000 9 17.38 0.51 3106.000 10 19.37 0.54 3931.000 11 21.57 0.58 4902.000 12 23.67 0.62 5947.000 13 25.76 0.65 7088.000 14 27.86 0.69 8319.000 15 29.74 0.73 9639.000 16 32.15 0.78 11116.000 Mi 17 33.82 0.82 12595.000 18 35.40 0.85 13997.000 19 37.49 0.88 15816.000 20 39.48 0.9 18397.000 21