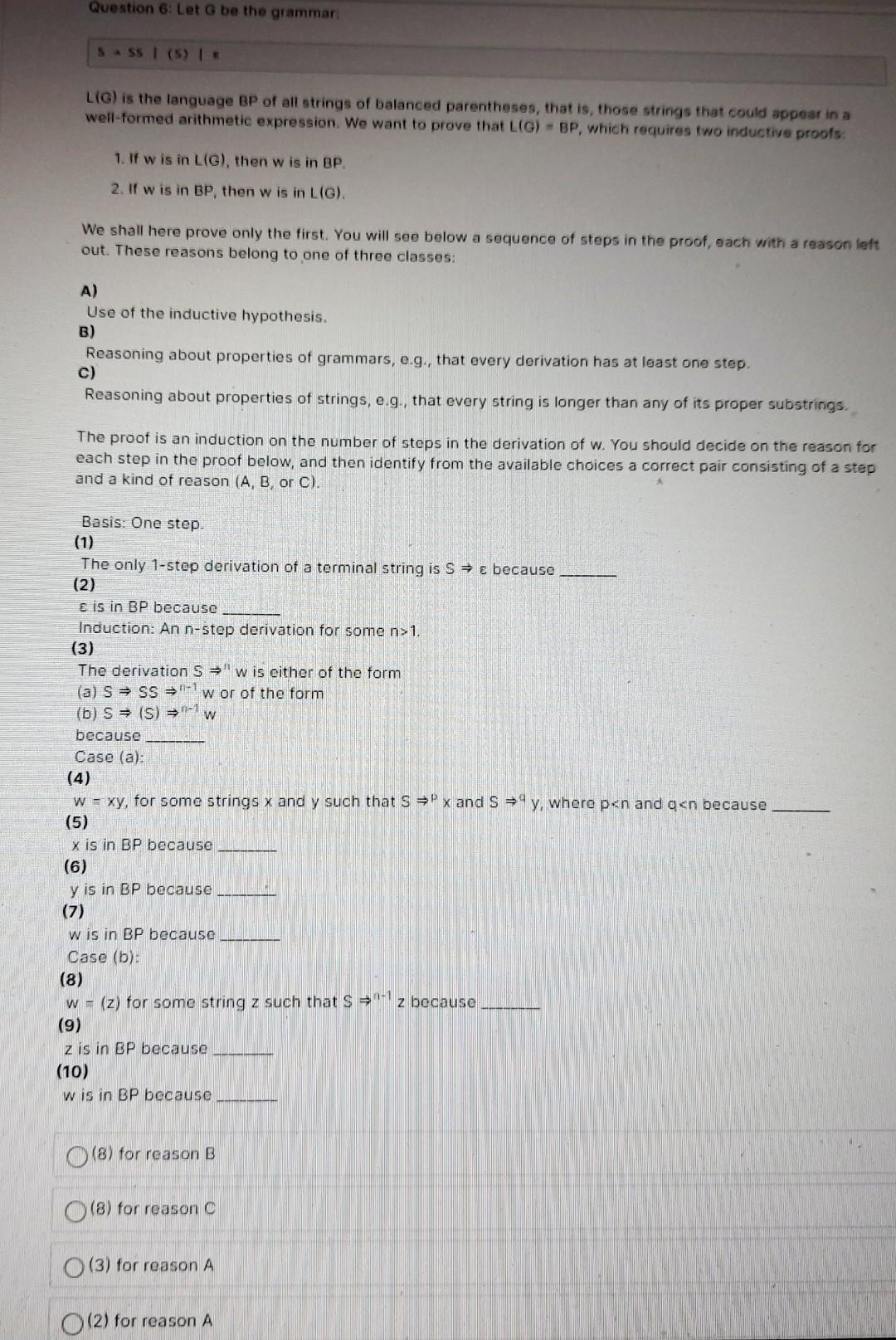
Question 6: Let G be the grammar S 55 I (5) LIG) is the language BP of all strings of balanced parentheses, that is, those strings that could appear in a well-formed arithmetic expression. We want to prove that LIG) - BP, which requires two inductive proofs. 1. If w is in LIG), then w is in BP. 2. If w is in BP, then w is in LIG). We shall here prove only the first. You will see below a sequence of steps in the proof, each with a reason left out. These reasons belong to one of three classes: A) Use of the inductive hypothesis. B) Reasoning about properties of grammars, e.g., that every derivation has at least one step. c) Reasoning about properties of strings, e.g., that every string is longer than any of its proper substrings. The proof is an induction on the number of steps in the derivation of w. You should decide on the reason for each step in the proof below, and then identify from the available choices a correct pair consisting of a step and a kind of reason (A, B, or C). Basis: One step. (1) The only 1-step derivation of a terminal string is S = E because (2) E is in BP because Induction: An n-step derivation for some ns1. (3) The derivation Swis either of the form (a) S = SS="w or of the form (b) S = (S) = -1 W because Case (a): (4) w - xy, for some strings x and y such that S = x and S = y, where pn and qn because (5) xis in BP because (6) y is in BP because (7) w is in BP because Case (b): (8) W = (z) for some string z such that S =- z because (9) z is in BP because (10) wis in BP because (8) for reason B (8) for reason c (3) for reason A (2) for reason A