question 6 please answer will upvote

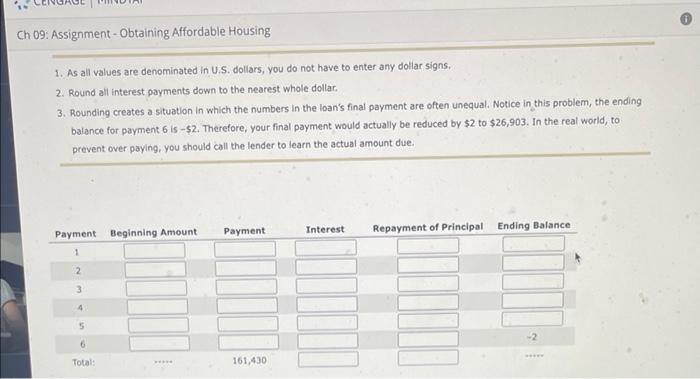
6. The mathematics of mortgage loans - Part 2 The Mathematics of Mortgage Loans In general, a mortgage loan is repaid monthly over the term of loan using the process of amortization, in which each payment contains two components: the interest that is owed on the debt outstanding and the portion of the principal that is being repaid. An amortization table or schedule details the monthly payments, the portions that will be used to pay the accrued interest and the repayment of the principal, and the debt remaining after each payment is made over the life of the loan You will start by constructing an amortization schedule. Your dream is finally coming truel You've saved and saved and are about to become a homeowner After a conversation with your banker, you've agreed to a 20% down payment on your $182,188 home. To keep this problem and your calculations relatively brief, assume that the bank has offered you a mortgage loan for $145,750 that 6% interest rate, semiannual payments of $26,905 and a 3-year term. Remember, the process is the same when you are preparing for either 6 semiannual payments of nearly $27,000 or 360 monthly payments of $873.85 for a 30-year conventional mortgage. Complete the following loan amortization table by entering the correct answers Notes Ch 09: Assignment - Obtaining Affordable Housing 1. As all values are denominated in U.S. dollars, you do not have to enter any dollar signs. 2. Round all interest payments down to the nearest whole dollar. 3. Rounding creates a situation in which the numbers in the loan's final payment are often unequal. Notice in this problem, the ending balance for payment 6 is -$2. Therefore, your final payment would actually be reduced by $2 to $26,903. In the real world, to prevent over paying, you should call the lender to learn the actual amount due Interest Payment Ending Balance Repayment of Principal Payment Beginning Amount 1 2 3 4 5 6 Total: 161,430 The total of the Interest column indicates the amount of interest expected to be paid over the life of the loan, and the sum of the Payment column detalls the total paid ($161,430) to purchase your $145,750 home. This is an amortized loan, because its payments contain: O Both interest and principal Only the principal that must be repaid Only accrued interest The monthly payment in the loan here is influenced by 3 variables: the amount borrowed, the loan's interest rate, and the term What is the nature of the relationship between each of these variables and the size of a loan's payment, everything else assumed to remain constant? . An increase in the amount borrowed will . An increase in the loan's interest rate will the size of the borrower's monthly payment the size of the borrower's monthly payment. the size of the borrower's monthly payment An increase in the loan's term will