Question
Question: An oil company produces oil from two wells. Well 1 can produce up to 150,000 barrels per day, and well 2 can produce up
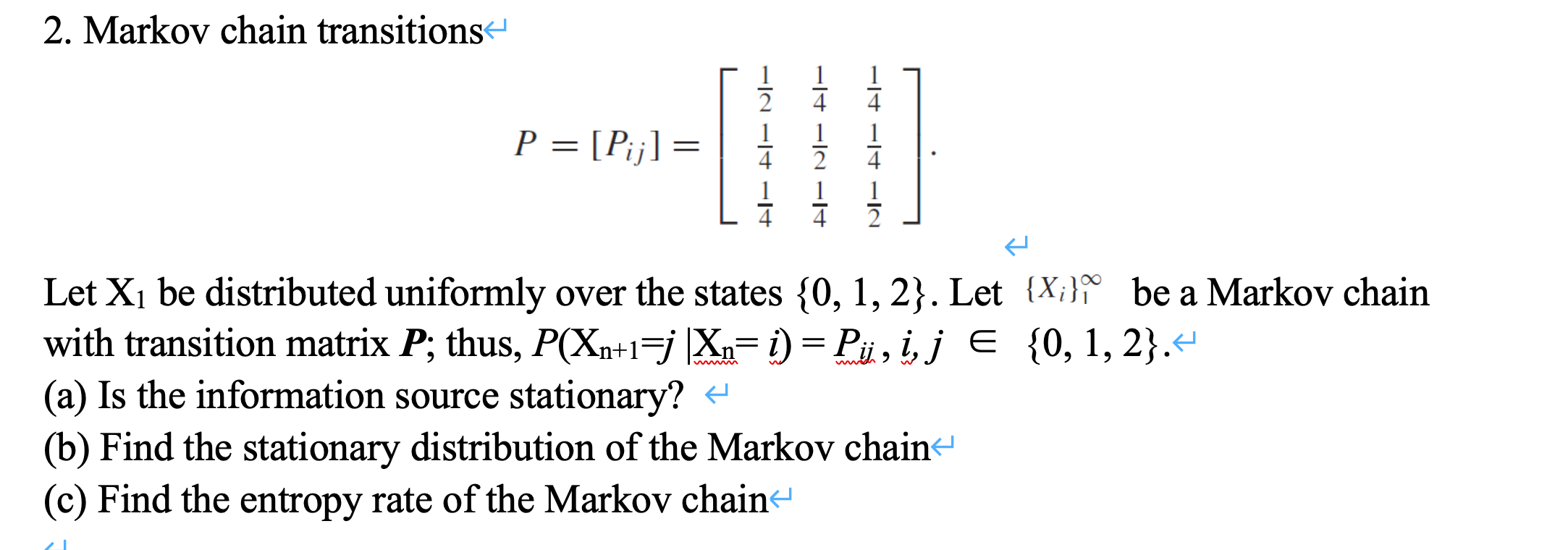
Question:
An oil company produces oil from two wells. Well 1 can produce up to 150,000 barrels per day, and well 2 can produce up to 200,000 barrels per day. It is possible to ship oil directly from the wells to the company's customers in Los Angeles and New York. Alternatively, the company could transport oil to the ports of Mobile and Galveston and then ship it by tanker to New York or Los Angeles, respectively. Los Angeles requires 160,000 barrels per day, and New York requires 140,000 barrels per day. The costs of shipping 1000 barrels between various locations are shown in the file P14_88.xlsx, where a blank indicates shipments that are not allowed. Determine how to minimize the transport costs in meeting the oil demands of Los Angeles and New York.


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


