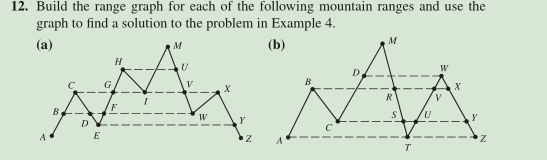
Question: question (b). plea 12. Build the range graph for each of the following mountain ranges and use the graph to find a solution to the
 question (b). plea
question (b). plea



12. Build the range graph for each of the following mountain ranges and use the graph to find a solution to the problem in Example 4 Example 4: Mountain Climbers Puzzle Two people start at locations A and Z at the same elevation on opposite sides of a mountain range whose summit is labeled M. See Figure 1.13a. We pose the following puzzle: is it possible for the people to move along the range in Figure 1.13a to meet at M in a fashion so that they are always at the same altitude every moment? We shall show this is possible for any mountain range like Figure 1.13a. The one assumption we make is that there is no point lower than A (or Z) and no point higher than M. We make a range graph whose vertices are pairs of points (PL., PR) at the same altitude with Pt on the left side of the summit and PR on the right side, such that one of the two points is a local peak or valley (the other point might also be a peak or (M, M) (E, W) C, X) (C, T) (C, V) (D, Y) (D, U) (B. U) (A, Z) Figure 1.13 valley). The vertices for the range in Figure 1.13a are shown in the graph in Figure 1 . 13b. We make an edge joining vertices (PL. PR) and (PL . PR) if the two people can move constantly in the same direction (both going up or both going down) from point PL to point Pt and from PR to PR, respectively. Our question now: is there a path in the range graph from the starting vertex (A, Z) to the summit vertex (M, M)? For the graph in Figure 1.13b, the answer is obviously yes. We claim that vertices (A, Z) and (M, M) in any range graph have degree 1, whereas every other vertex in the range graph has degree 2 or 4. (A, Z) has degree 1 because when both people start clim they have no choice initially but to climb upward until one arrives at a peak. In Figure 1.13a, the first peak encountered is C on the left, and so the one edge from (A, Z) goes to (C, X). A similar argument applies at (M, M). Next consider a vertex (PL, PR) where one point is a peak and the other point is neither peak nor valley, such as (E, W). From the peak we can go down in either direction: at W, we can go down toward Z or toward U. In either direction, the people go until one (or both) reaches a valley. At (E, W), the two edges go to (D, Y) and (D, U). Thus such a vertex has degree 2. A similar argument applies if one point (but not both) is a valley. It is left as an exercise for the reader to show that if a vertex (PL, PR) consists of two peaks or two valleys, such as (D, U), it will have degree 4. (A vertex consisting of a valley and a peak will have degree 0-why?) ing up the range from their respective sides, Suppose there were no path from (A. Z) to (M, M) in the range graph. Thus, these two vertices are in different components of the range graph. We use the fact that starting vertex (A, Z) and summit vertex (M, M) are the only vertices of odd degree to obtain a contradiction. The component of the range graph consisting of (A, Z) and all the vertices that can be reached from (A, Z) would form a graph with just one vertex of odd degree, namely, (A, Z). This contradicts the Corollary, and so any range graph must have a path from (A, Z) to (M, M). Many interesting properties in graph theory are dependent on certain sets of edges having even size. Euler cycles, discussed in Section 2.1, arise when all vertices have even degree In Example 2 of Section 1.1, we considered a matching problem involving the graph shown in Figure 1.14. The vertices on the left represented people and the vertices on the right represented jobs. An edge links a left vertex to a right vertex to indicate 1.3 Edge Counting 27 Figure 1.14 E that a certain person can perform a certain job. There can never be an edge between two vertices on the left or between two vertices on the right. Such a graph is called a bipartite graph. Formally, a graph G is bipartite if its vertices can be partitioned into two sets V and V2 and every edge joins a vertex in Vi with a vertex in V2 Bipartite graphs can be characterized by all circuits in such graphs having even length (if there are no circuits, the graph is also bipartite), where the length of a circuit or path is the number of edges in it. Theorem 2 A graph G is bipartite if and only if every circuit in G has even length. Proof Note that it is sufficient to prove this theorem for connected bipartite graphs. We claim that if the theorem is true for each connected component of a disconnected bipartite graph G, then it is true for G (components were formally defined just above Example 4). This claim follows from G's being bipartite if and only if each of its components is bipartite, and any circuit in G's having even length if and only if any circuit in each of its components has even length. First we show that if G is bipartite, then any circuit has an even length. If G is bipartite so that it can be drawn with all edges connecting a left vertex with a right vertex, then any circuit xi-x2-13.--i has alternately a left vertex, then a right vertex, then a left vertex, and so on, assuming the first vertex x1 is on the left. Odd subscripted vertices are on the left, and even-subscripted vertices on the right. See Figure 1.15a. Since x is adjacent to xi, Xn must be on the right, so its subscript is even. That is, there are an even number of vertices in the circuit. Any circuit has the same number of edges as vertices, and thus this circuit has even length *1 r6 Figure 1.15 Suppose next that any circuit in G (there may be no circuits) has even length. We show how to construct a bipartite arrangement of G. We use the AC Principle and assume that a bipartition exists, and use properties of that bipartition to construct it. Take any given vertex, call it a, and put it on the left. Put all vertices adjacent to a on the right. Next put all vertices that are two edges away from a, that is, at the end of some path of length 2 from a, on the left. In general, if there is a path of odd length between a and a vertex x, put x on the right. If there is a path of even length between a and x, put x on the left. There cannot be distinct paths P and P between a and x of odd and of even lengths, respectively, since taking P from a to x and then returning to a on P yields an odd-length circuit. This is impossible, since all circuits have even length. (If P and P' have a vertex q in common besides a and x, then a further argument is needed to show that there is a circuit of odd length. See Exercise 15 for details.) Similarly, we argue that there cannot be an edge between two vertices, say, b and c, both on the left. There must exist even-length paths . Q' joining a with b and c, respectively (since b and c are on the left). See Figure 1.15b, in which Q is dashed and Q' is dotted. Observe that Q' followed by the edge (c, b) yields an odd-length path from a to b. This is impossible, since we just proved that there cannot be both an even-length path (Q) and an odd-length path (Q' plus (a, b)) from a to any other vertex in G. By similar reasoning, two vertices on the right cannot be adjacent. Thus, we have a bipartite arrangement of G. 12. Build the range graph for each of the following mountain ranges and use the graph to find a solution to the problem in Example 4 Example 4: Mountain Climbers Puzzle Two people start at locations A and Z at the same elevation on opposite sides of a mountain range whose summit is labeled M. See Figure 1.13a. We pose the following puzzle: is it possible for the people to move along the range in Figure 1.13a to meet at M in a fashion so that they are always at the same altitude every moment? We shall show this is possible for any mountain range like Figure 1.13a. The one assumption we make is that there is no point lower than A (or Z) and no point higher than M. We make a range graph whose vertices are pairs of points (PL., PR) at the same altitude with Pt on the left side of the summit and PR on the right side, such that one of the two points is a local peak or valley (the other point might also be a peak or (M, M) (E, W) C, X) (C, T) (C, V) (D, Y) (D, U) (B. U) (A, Z) Figure 1.13 valley). The vertices for the range in Figure 1.13a are shown in the graph in Figure 1 . 13b. We make an edge joining vertices (PL. PR) and (PL . PR) if the two people can move constantly in the same direction (both going up or both going down) from point PL to point Pt and from PR to PR, respectively. Our question now: is there a path in the range graph from the starting vertex (A, Z) to the summit vertex (M, M)? For the graph in Figure 1.13b, the answer is obviously yes. We claim that vertices (A, Z) and (M, M) in any range graph have degree 1, whereas every other vertex in the range graph has degree 2 or 4. (A, Z) has degree 1 because when both people start clim they have no choice initially but to climb upward until one arrives at a peak. In Figure 1.13a, the first peak encountered is C on the left, and so the one edge from (A, Z) goes to (C, X). A similar argument applies at (M, M). Next consider a vertex (PL, PR) where one point is a peak and the other point is neither peak nor valley, such as (E, W). From the peak we can go down in either direction: at W, we can go down toward Z or toward U. In either direction, the people go until one (or both) reaches a valley. At (E, W), the two edges go to (D, Y) and (D, U). Thus such a vertex has degree 2. A similar argument applies if one point (but not both) is a valley. It is left as an exercise for the reader to show that if a vertex (PL, PR) consists of two peaks or two valleys, such as (D, U), it will have degree 4. (A vertex consisting of a valley and a peak will have degree 0-why?) ing up the range from their respective sides, Suppose there were no path from (A. Z) to (M, M) in the range graph. Thus, these two vertices are in different components of the range graph. We use the fact that starting vertex (A, Z) and summit vertex (M, M) are the only vertices of odd degree to obtain a contradiction. The component of the range graph consisting of (A, Z) and all the vertices that can be reached from (A, Z) would form a graph with just one vertex of odd degree, namely, (A, Z). This contradicts the Corollary, and so any range graph must have a path from (A, Z) to (M, M). Many interesting properties in graph theory are dependent on certain sets of edges having even size. Euler cycles, discussed in Section 2.1, arise when all vertices have even degree In Example 2 of Section 1.1, we considered a matching problem involving the graph shown in Figure 1.14. The vertices on the left represented people and the vertices on the right represented jobs. An edge links a left vertex to a right vertex to indicate 1.3 Edge Counting 27 Figure 1.14 E that a certain person can perform a certain job. There can never be an edge between two vertices on the left or between two vertices on the right. Such a graph is called a bipartite graph. Formally, a graph G is bipartite if its vertices can be partitioned into two sets V and V2 and every edge joins a vertex in Vi with a vertex in V2 Bipartite graphs can be characterized by all circuits in such graphs having even length (if there are no circuits, the graph is also bipartite), where the length of a circuit or path is the number of edges in it. Theorem 2 A graph G is bipartite if and only if every circuit in G has even length. Proof Note that it is sufficient to prove this theorem for connected bipartite graphs. We claim that if the theorem is true for each connected component of a disconnected bipartite graph G, then it is true for G (components were formally defined just above Example 4). This claim follows from G's being bipartite if and only if each of its components is bipartite, and any circuit in G's having even length if and only if any circuit in each of its components has even length. First we show that if G is bipartite, then any circuit has an even length. If G is bipartite so that it can be drawn with all edges connecting a left vertex with a right vertex, then any circuit xi-x2-13.--i has alternately a left vertex, then a right vertex, then a left vertex, and so on, assuming the first vertex x1 is on the left. Odd subscripted vertices are on the left, and even-subscripted vertices on the right. See Figure 1.15a. Since x is adjacent to xi, Xn must be on the right, so its subscript is even. That is, there are an even number of vertices in the circuit. Any circuit has the same number of edges as vertices, and thus this circuit has even length *1 r6 Figure 1.15 Suppose next that any circuit in G (there may be no circuits) has even length. We show how to construct a bipartite arrangement of G. We use the AC Principle and assume that a bipartition exists, and use properties of that bipartition to construct it. Take any given vertex, call it a, and put it on the left. Put all vertices adjacent to a on the right. Next put all vertices that are two edges away from a, that is, at the end of some path of length 2 from a, on the left. In general, if there is a path of odd length between a and a vertex x, put x on the right. If there is a path of even length between a and x, put x on the left. There cannot be distinct paths P and P between a and x of odd and of even lengths, respectively, since taking P from a to x and then returning to a on P yields an odd-length circuit. This is impossible, since all circuits have even length. (If P and P' have a vertex q in common besides a and x, then a further argument is needed to show that there is a circuit of odd length. See Exercise 15 for details.) Similarly, we argue that there cannot be an edge between two vertices, say, b and c, both on the left. There must exist even-length paths . Q' joining a with b and c, respectively (since b and c are on the left). See Figure 1.15b, in which Q is dashed and Q' is dotted. Observe that Q' followed by the edge (c, b) yields an odd-length path from a to b. This is impossible, since we just proved that there cannot be both an even-length path (Q) and an odd-length path (Q' plus (a, b)) from a to any other vertex in G. By similar reasoning, two vertices on the right cannot be adjacent. Thus, we have a bipartite arrangement of G
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


