Question:
The personnel department of a large corporation wants to estimate the family dental expenses of its employees to determine the feasibility of providing a dental insurance plan. A random sample of 12 employees reveals the following family dental expenses (in dollars).
dental expense data.xlsx 115 370 250 593 540 225 177 425 318 182 275 228
Construct a 93% confidence interval estimate for the mean of family dental expenses for all employees of this corporation.
Place your LOWER limit, in dollars rounded to 1 decimal place, in the first blank. Do not use a dollar sign, a comma, or any other stray mark. For example, 98.4 would be a legitimate entry.___
Place your UPPER limit, in dollars rounded to 1 decimal place, in the second blank. Do not use a dollar sign, a comma, or any other stray mark. For example, 567.8 would be a legitimate entry.
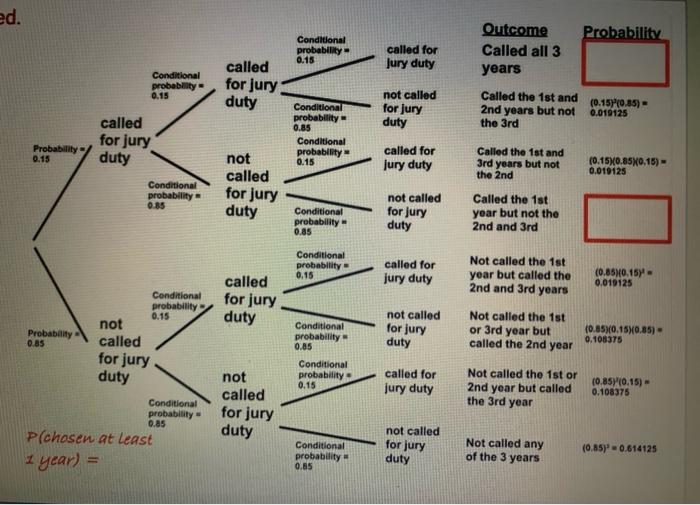
Name For the following word problems state if the problem requires using the Central Limit theorem or if does Not require using the Central limit theorem Circle the correct choice: 1. What is the probability of randomly selecting an adult with an IQ score less than 75? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 2. If 30 cell phones are randomly selected what is the probability the cell phones will last an average of more than 23.8 months? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 3. In general Marine platoons are around 50 strong, if a sample of a given platoon is taken from a population of Marines with a mean weight of 200 pounds and with standard deviation o = 10. What is the probability that the sample mean weight will be less than 196 pounds? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 4. The mean age of baseball players is 27 years. Assuming the age of baseball players are normally distributed and that the average size of a baseball team is 25 players, what is the probability a baseball player is older than 30 years if the player is randomly selected. A. Requires the Central limit theorem. B. Does not require the central limit theorem. 5. Suppose that you have a sample of 81 students from a population with mean u = 500 and with standard deviation o = 108. What is the probability that the sample mean will be greater than 483. A. Requires the Central limit theorem. B. Does not require the central limit theorem. Page 1 of 1In each situation below, is it reasonable to use a binomial distribution for the random variable X? Give reasons for your answerin each case. {a} A random sample of students in a fitness study. X is the mean systolic blood pressure of the sample. tries, a binomial distnbution is reasonable. X can only take on two values No, a binomial distnbution is not reasonable. X is not a count of successes. No; a binomial tstribution is not reasonable. Binomial distnbutions cannot be used with random samples No, a binomial tstribution is not reasonable. it should be associated with a population \"ms a binomial tstribution is reasonable. X is a mean of the binomial distribution. [bi A manufacturer of running shoes picks a random sample o'fthe production of shoes each day for a detailed inspection. Today's sample of 20 pairs of shoes indudes 1 pairwith a defect. No; a binomial bstribution is not reasonable. Dne defect in a sample of 2B is not a large enough percentage. No, a binomial distribution is not reasonable. Binomial distributions cannot be used with random samples. \"ms a binomial distribution is reasonable. p is the probability of a defective pair. "ms a binomial distribution is reasonable. p is the number of defective shoes from today's sample. No, a binomial distribution is not reasonable. Cine defect is not a large enough count. {c} A nutrition study d'iooses an SR5 of college students Tl'iey are asked whether or not they usually eat at least ve servings of fruits or vegetables per day. X is the nurrberwho saythat they do. \"lies; a binomial distribution is reasonable. n is the number of students chosen from the sample and X is the number of servings of fmits and vegetables they eat. No, a binomial tstribuijon is not reasonable. A student might eat less than ve senaings offnJits and vegetables but could daim othenlvise. Yes, a binomial distnbution is reasonable. p is the percentage of students d'iosen from the population and n is the number of servings of fmits. and vegetables they eat. Yes, a binomial distnbution is reasonable. n is the number of students in the sample and p is the probabilitythat a student eats at least five servings o'ffruits and vegetables No, a binomial tstribution is not reasonable. Binomial distnbutions cannot be used with random samples ed. Outcome Probability Conditional probability = called for Called all 3 0.15 called Jury duty years Conditional probability for jury 0.15 not called Called the 1st and duty (0.15)10.85) - Conditional for Jury 2nd years but not 0.019125 called probability = duty the 3rd 0.85 for jury Conditional Probability probability called for Called the ist and 0.15 duty not 0.15 jury duty 3rd years but not (0.15)(0.85)(0,15)= called the 2nd 0.019125 Conditional probability for jury not called Called the 1st 0-85 duty Conditional for jury year but not the probability = duty 2nd and 3rd 0.85 Conditional called for Not called the 1st probability = 0.15 year but called the (0.85)10.15)= called jury duty 0,019125 2nd and 3rd years Conditional for jury probability 0.15 duty not called Not called the ist not Conditional for jury or 3rd year but (0.85)(0.15)(0.85)- Probability probability = 0. 108375 0.85. called 0.85 duty called the 2nd year for jury Conditional duty not probability called for Not called the ist or (0.85) (0.15)- 0.15 called jury duty 2nd year but called 0.108375 Conditional the 3rd year probability = for jury 0.85 not called P(chosen at least duty Conditional for jury Not called any (0.8513 - 0.614125 probability = duty of the 3 years 1 year ) = 0.85In each situation below, is it reasonable to use a binomial distribution for the random variable &7 Give reasons for your answer in each case. (a) A random sample of students in a fitness study. X is the mean systolic blood pressure of the sample. Yes, a binomial distribution is reasonable. & is a mean of the binomial distribution. No, a binomial distribution is not reasonable. Binomial distributions cannot be used with random samples. Yes, a binomial distribution is reasonable. X can only take on two values. No, a binomial distribution is not reasonable. X should be associated with a population. ()No, a binomial distribution is not reasonable. X is not a count of successes. (b] A manufacturer of running shoes picks a random sample of the production of shoes each day for a detailed inspection. Today's sample of 20 pairs of shoes includes 1 pair with a defect. No, a binomial distribution is not reasonable. Binomial distributions cannot be used with random samples. No, a binomial distribution is not reasonable. One defect is not a large enough count. Yes, a binomial distribution is reasonable. p is the probability of a defective pair. No, a binomial distribution is not reasonable. One defect in a sample of 20 is not a large enough percentage. Yes, a binomial distribution is reasonable. p is the number of defective shoes from today's sample. (c) A nutrition study chooses an SRS of college students. They are asked whether or not they usually eat at least five servings of fruits or vegetables per day. X is the number who say that they do. ) No, a binomial distribution is not reasonable. Binomial distributions cannot be used with random samples. Yes, a binomial distribution is reasonable. on is the number of students chosen from the sample and X is the number of servings of fruits and vegetables they cat. Yes, a binomial distribution is reasonable. In is the number of students in the sample and p is the probability that a student eats at least five servings of fruits and vegetables. ) No, a binomial distribution is not reasonable. A student might eat less than five servings of fruits and vegetables but could claim otherwise. Yes, a binomial distribution is reasonable. p is the percentage of students chosen from the population and a is the number of servings of fruits and vegetables they eat