question2.........

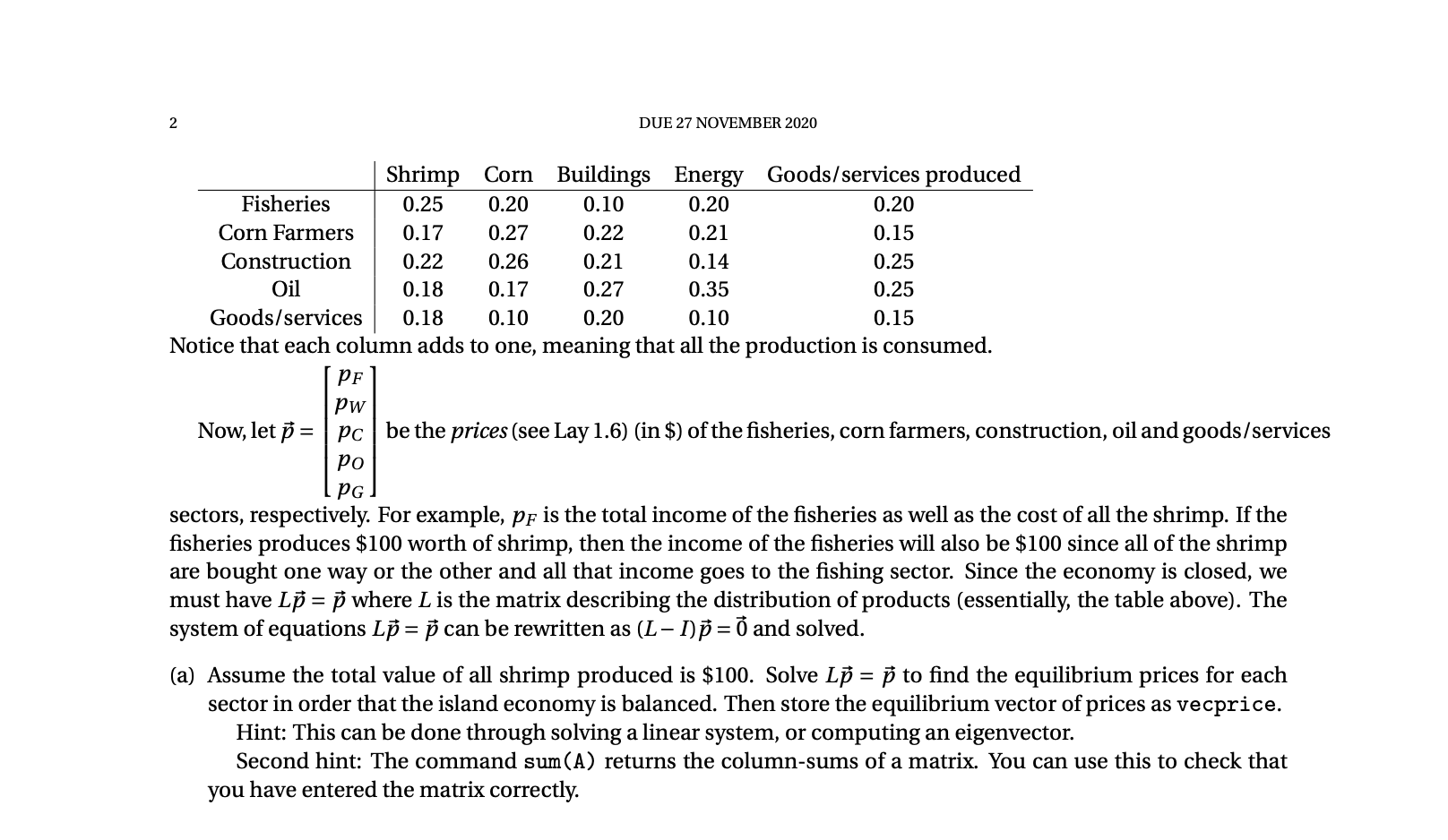
QUESTION 2: INPUT-OUTPUT MODELS IN ECONOMICS We will consider a simple economic model (see Iay 1,6). Consider a closed economy with distinct economic sectors: shrimp shing, corn farming, construction (of buildings), oil (for energy) and goods/services. Assume that there are no imports or exports from the island and that everything that is produced is consumed. This is called a closed-exchange modelz. Each sector of the economy uses products of the various sectors as follows (note that each sector also consumes some of its own outputs - for instance, the sherfolk eat some shrimp themselves). 1Note that we are ignoring male insects here all adults in this model can produce eggs, and all surviving eggs grow up to become egg- produoers. See https :lluw . ramas . com/modeling-tips old for a discussion of shortcomings in population models. 2Models of this general type are also called Montiquodek after the Russian-American economist W. Leontief [1906-1999) who won the Nobel Prize in economics in 1973. 2 DUE 27 NOVEMBER 2020 Shrimp Corn Buildings Energy Goods/services produced Fisheries 0.25 0.20 0.10 0.20 0.20 Corn Farmers 0.17 0.27 0.22 0.21 0.15 Construction 0.22 0.26 0.21 0.14 0.25 Oil 0.18 0.17 0.27 0.35 0.25 Goods/services 0.18 0.10 0.20 0.10 0.15 Notice that each column adds to one, meaning that all the production is consumed. PF PW Now, let p = pc be the prices (see Lay 1.6) (in $) of the fisheries, corn farmers, construction, oil and goods/services po L PG ] sectors, respectively. For example, pp is the total income of the fisheries as well as the cost of all the shrimp. If the fisheries produces $100 worth of shrimp, then the income of the fisheries will also be $100 since all of the shrimp are bought one way or the other and all that income goes to the fishing sector. Since the economy is closed, we must have Lp = p where L is the matrix describing the distribution of products (essentially, the table above). The system of equations Lp = p can be rewritten as (L- D)p = 0 and solved. (a) Assume the total value of all shrimp produced is $100. Solve Lp = p to find the equilibrium prices for each sector in order that the island economy is balanced. Then store the equilibrium vector of prices as vecprice. Hint: This can be done through solving a linear system, or computing an eigenvector. Second hint: The command sum (A) returns the column-sums of a matrix. You can use this to check that you have entered the matrix correctly