Questions: Give brief explanation and Solution.
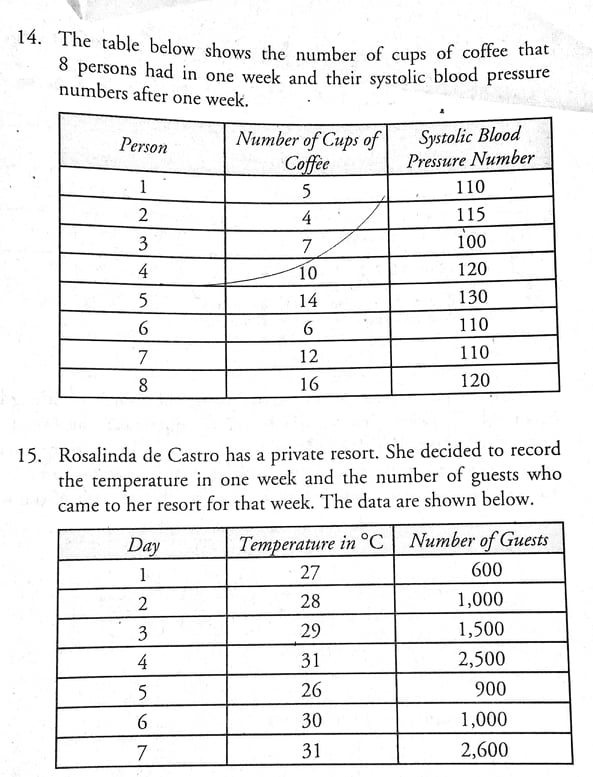
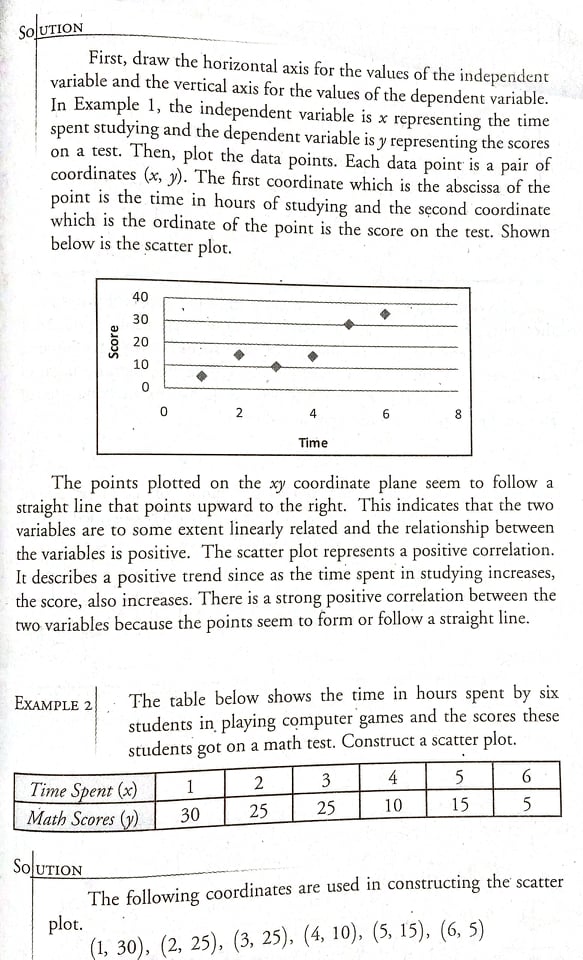
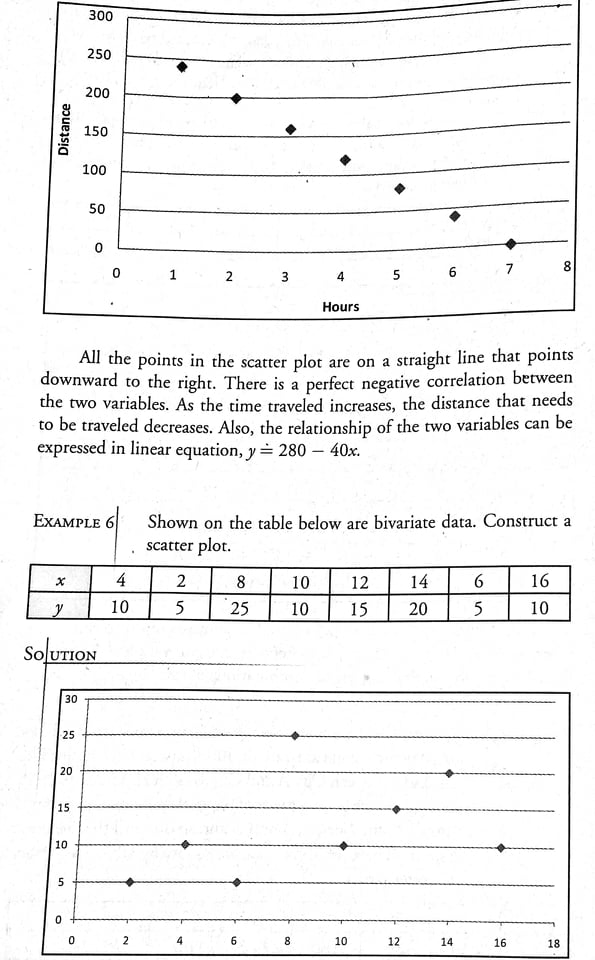
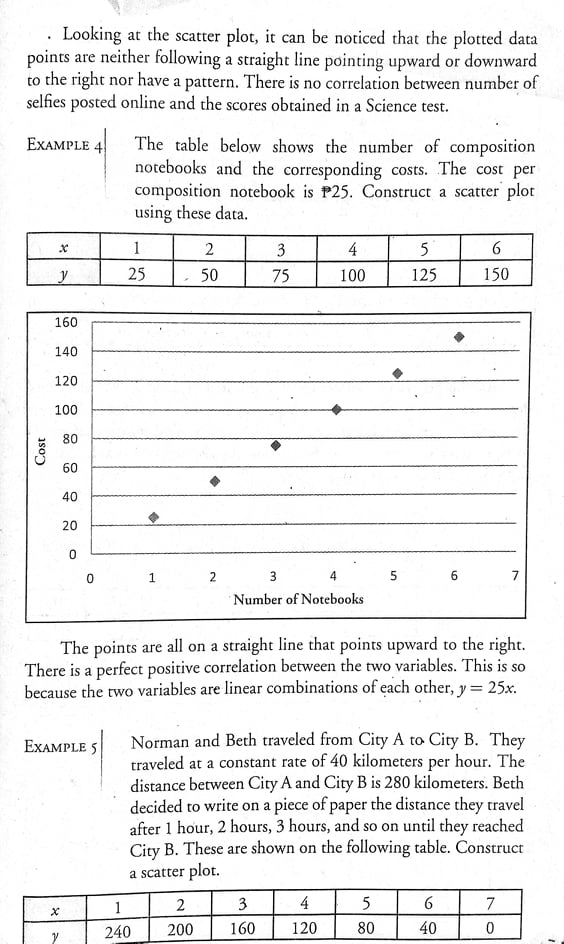
._ 1 \\IL In Example 6, the points in the scatter plot seem to follow a Straight . line that points upward to the right at certain intervals. However, it cannot be said that the correlation is perfect positive not even moderately positive. There is a weak positive correlation between the two variables because the data points are widely spread and far From the straight line they seem to follow. The strength of association between the two variables on the scatter plot can be estimated by observing the dots. If the dots are on a straight line pointing upward to the right, then there is a pcrfccrporiricc correlation. If the dots are on the_ straight line pointing downward to the right, then there is a pacier negative correlation. If the dots are concentrated around a straight line pointing upward to the right then there is a strongpositinc correlation. If the dots are concentrated around the straight line pointing downward to the right then there is a strong negative correlation. If the dots are not close but are not too far from the straight line that they Seem to follow then there is a modcrorc; panties or modcrorciy negative correlation depending on the direction of the straight line. If the dots in the scatter plot are widely spread just like in Example 6, then the correlation is weak. MATHgroupie For exercises 11-15, do the following: a. Identify the independent variable and the dependent variable. b. Construct a scatter plot. c. Determine the direction of the straight line that the data points seem to follow. d. Determine the strength of correlation between the two variables. 11. The table shows the number of hours spent by 8 students in using the Internet and their scores on a Mathematics test. Student Hours Using the Internet Scores 1 1 30 2 N 25 3 20 A 2 30 0.5 26 2.5 15 2 32 3 1514. The table below shows the number of cups of coffee that 8 persons had in one week and their systolic blood pressure numbers after one week. Person Number of Cups of Systolic Blood Coffee Pressure Number 1 5 110 2 4 115 7 100 10 120 UI 14 130 6 110 7 12 110 8 16 120 15. Rosalinda de Castro has a private resort. She decided to record the temperature in one week and the number of guests who came to her resort for that week. The data are shown below. Day Temperature in C Number of Guests 1 27 600 2 28 1,000 29 1,500 31 2,500 26 900 6 30 1,000 7 31 2,600SOLUTION First, draw the horizontal axis for the values of the independent variable and the vertical axis for the values of the dependent variable. In Example 1, the independent variable is x representing the time spent studying and the dependent variable is y representing the scores on a test. Then, plot the data points. Each data point is a pair of coordinates (x, y). The first coordinate which is the abscissa of the point is the time in hours of studying and the second coordinate which is the ordinate of the point is the score on the test. Shown below is the scatter plot. 40 30 Score 20 10 0 0 2 4 6 8 Time The points plotted on the xy coordinate plane seem to follow a straight line that points upward to the right. This indicates that the two variables are to some extent linearly related and the relationship between the variables is positive. The scatter plot represents a positive correlation. It describes a positive trend since as the time spent in studying increases, the score, also increases. There is a strong positive correlation between the two variables because the points seem to form or follow a straight line. EXAMPLE 2 The table below shows the time in hours spent by six students in playing computer games and the scores these students got on a math test. Construct a scatter plot. Time Spent (x) 1 2 3 4 5 6 5 Math Scores (y) 30 25 25 10 15 SOLUTION The following coordinates are used in constructing the scatter plot. (1, 30), (2, 25), (3, 25), (4, 10), (5, 15), (6, 5)300 250 200 Distance 150 100 50 0 0 6 8 1 2 3 4 5 Hours All the points in the scatter plot are on a straight line that points downward to the right. There is a perfect negative correlation between the two variables. As the time traveled increases, the distance that needs to be traveled decreases. Also, the relationship of the two variables can be expressed in linear equation, y = 280 - 40x. EXAMPLE 6 Shown on the table below are bivariate data. Construct a scatter plot. X 4 2 8 10 12 14 6 16 10 5 25 10 15 20 5 10 SO UTION 30 25 20 15 10 0 2 4 6 8 10 12 14 16 18. Looking at the scatter plot, it can be noticed that the plotted data points are neither following a straight line pointing upward or downward to the right nor have a pattern. There is no correlation between number of selfies posted online and the scores obtained in a Science test. EXAMPLE 4 The table below shows the number of composition notebooks and the corresponding costs. The cost per composition notebook is P25. Construct a scatter plot using these data. X 1 2 3 4 5 6 y 25 50 75 100 125 150 160 140 120 100 80 Cost 60 40 20 0 1 2 3 4 5 6 7 Number of Notebooks The points are all on a straight line that points upward to the right. There is a perfect positive correlation between the two variables. This is so because the two variables are linear combinations of each other, y = 25x. EXAMPLE 5 Norman and Beth traveled from City A to City B. They traveled at a constant rate of 40 kilometers per hour. The distance between City A and City B is 280 kilometers. Beth decided to write on a piece of paper the distance they travel after 1 hour, 2 hours, 3 hours, and so on until they reached City B. These are shown on the following table. Construct a scatter plot. X 2 3 4 5 6 IN 240 200 160 120 80 40 0Scatter Plots 6.1 Competencies M1 1/12SP-IVg-2, M11/12SP-IVg-3, M11/12SP-IVg-4, M11/12SP-IVh-1 The learner will be able to: 1. illustrate the nature of bivariate data; construct a scatter plot; describe shapes (form), trend ( direction), and variation ( strength) based on the scatter plot; and 4. estimate strength of association between the variables based on a scatter plot. Some research studies involve two variables. One of these two variables is the independent variable and the other one is the dependent variable. The independent variable is the variable that may affect the dependent variable to change. The dependent variable is the variable that is influenced or affected by the independent variable. The data collected in this type of study that involves two variables are called bivariate data. Bivariate data are always in pairs. For instance, a researcher wants to find out if there is a relationship between height and weight. Here, height is the independent variable and weight is the dependent variable. If a person gets taller, his weight may increase but an increase in his weight will not make the person taller. But this does not mean that this variable causes the other variable, it simply means that there is a significant association between the two. The heights of the students which may be in centimeters and the weights of the students which may be in kilograms are the bivariate data. Scatter plots are diagrams that are used to show the degree and pattern of relationship between the two sets of data. They are constructed on the xy coordinate plane. Each data point on a scatter plot represents two values (x, y). The abscissa of the point is a value of the independent variable x and the ordinate is a value of the dependent variable y. EXAMPLE I The table below shows the time in hours (x) spent by six grade 11 students in studying their lessons and their scores (y) on a test. Construct a scatter plot. Time Spent (x) 1 2 3 4 5 6 Score (y) 5 15 10 15 30 3512. The table below shows the number of hours spent in the mall by 12 persons and the amount of money they spent when they go to the mall. Amount Person Hours in the Mall of Money Spent (P ) 8 600 N 10 1000 9 500 3 600 200 7 900 6 500 800 5 500 10 2 150 11 3 450 12 4 650 13. Shown in the table below are the number of hours spent by 8 students in studying and their scores in a Mathematics test. Student Hours Spent Scores in Studying Mathematics Test 4 40 N 2 25 20 30 IN 20 25 20 4 3535 30 25 20 Score 15 10 0 0 H 3 5 6 7 Time The points seem to follow a straight line that points downward to the right. The scatter plot represents a negative correlation. It describes a negative trend since as the amount of time spent in playing computer games increases, the score in math decreases. There is a strong negative correlation between the two variables because the points are concentrated around the straight line they seem to follow. EXAMPLE 3 The table below shows the number of selfies (x) posted online of students and the scores (y) they obtained from a Science test. Construct a scatter plot. Number of Selfies (x) 2 3 4 5 6 Scores in Science Test (y) 25 5 20 40 25 9 SOLUTION 45 40 35 30 25 Test Scores 20 15 O U S 0 2 3 4 5 6 7 Number of Selfies Posted