Questions on microeconomics, try and provide a solution for these
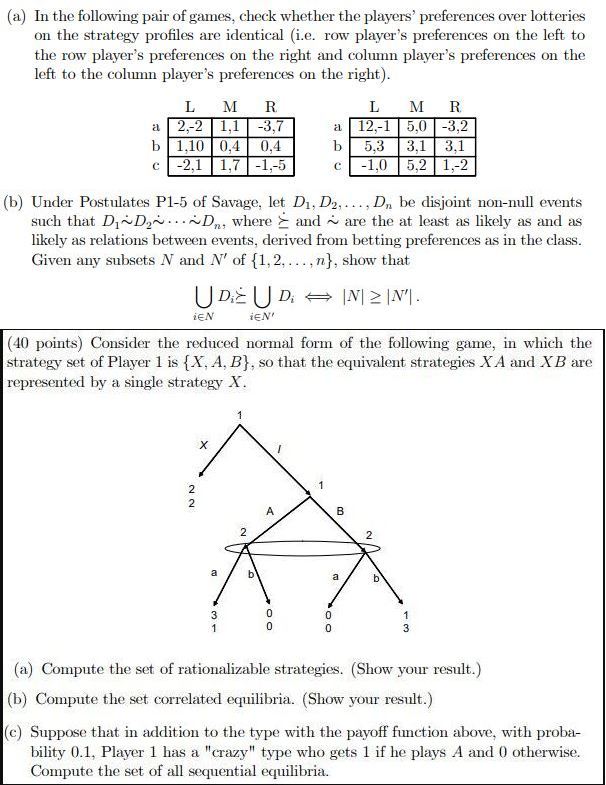
(a) In the following pair of games, check whether the players' preferences over lotteries on the strategy profiles are identical (i.e. row player's preferences on the left to the row player's preferences on the right and column player's preferences on the left to the column player's preferences on the right). L M R L M R 2.-2 1,1 -3,7 12.-1 5.0 -3,2 1,10 0,4 0,4 5.3 3,1 3.1 -2,1 1,7 -1,-5 -1,0 5.2 1,-2 (b) Under Postulates P1-5 of Savage, let D1, D2. .... D, be disjoint non-null events such that Di~Dy...~Dn, where > and ~ are the at least as likely as and as likely as relations between events, derived from betting preferences as in the class. Given any subsets N and N' of {1, 2. ....n}, show that UD UD - IN1 2 IN'. iEN iEN' (40 points) Consider the reduced normal form of the following game, in which the strategy set of Player 1 is {X, A, B}, so that the equivalent strategies X A and X B are represented by a single strategy X. X NO N 2 (a) Compute the set of rationalizable strategies. (Show your result.) (b) Compute the set correlated equilibria. (Show your result.) (c) Suppose that in addition to the type with the payoff function above, with proba- bility 0.1, Player 1 has a "crazy" type who gets 1 if he plays A and 0 otherwise. Compute the set of all sequential equilibria.(a) In the following pair of games, check whether the players' preferences over lotteries on the strategy profiles are identical (i.e. row player's preferences on the left to the row player's preferences on the right and column player's preferences on the left to the column player's preferences on the right). L M R. L M R. 2,-2 1,1 -3,7 12.-1 5.0 -3,2 b 1,10 0,4 0,4 b 5.3 3,1 3.1 -2,1 1,7 -1,-5 C -1.0 5.2 1.-2 (b) Under Postulates P1-5 of Savage, let D1, D2. . ... D,, be disjoint non-null events such that Dj~D,~ ~Do, where > and ~ are the at least as likely as and as likely as relations between events, derived from betting preferences as in the class. Given any subsets / and N' of {1, 2, ...,n}, show that UD UD - IN| 2 IN'. iEN iEN'(31] points} Consider an expected prot maximizing monopolist who faces an uncertain demand. He supplies q units of goods at zem cost and sells it at price 3 q, where H is nnlmown. [The price and the supply level can be negative] (11] Asemmhg that 3 ~ N {3:152}, compute the monopolist's uptilnal Suppl}...r q and his expected prot under the optimal supply. [h] Suppose that, through market research, the monopolist can learn about H. In particularT by investing :12, he can learn the value of a random variable 1' before charming his Suppl]? 1;, such that. H = X+Y, X ~ N [[1,]. c] and lr' ~ N[,c]. How much should the monopolist invest? [Note that the utility function of the monopolist is [H q] q 22.]