Questions on microeconomics, try and provide solutions for these.
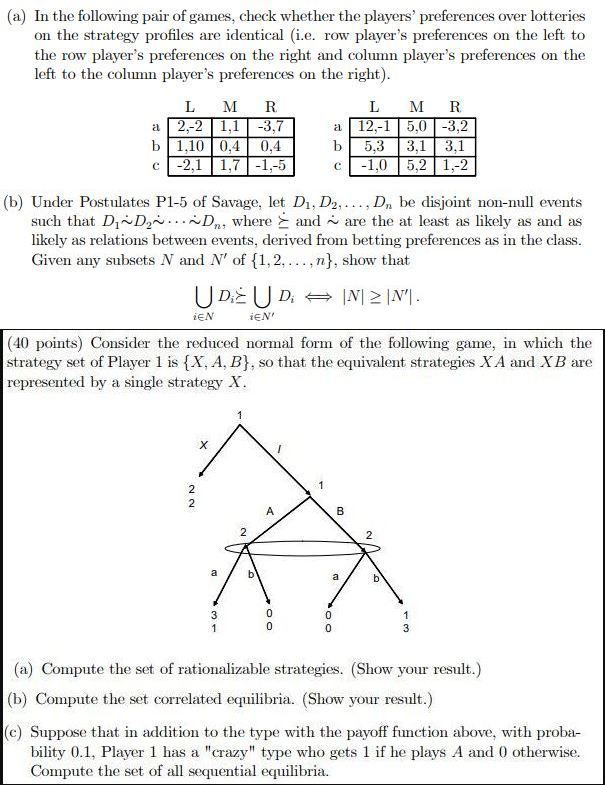
(a) In the following pair of games, check whether the players' preferences over lotteries on the strategy profiles are identical (i.e. row player's preferences on the left to the row player's preferences on the right and column player's preferences on the left to the column player's preferences on the right). L M R L M R 2.-2 1,1 -3,7 12.-1 5.0 -3,2 1,10 0,4 0,4 5.3 3,1 3.1 -2,1 1,7 -1,-5 -1,0 5.2 1,-2 (b) Under Postulates P1-5 of Savage, let D1, D2. .... D, be disjoint non-null events such that Di~Dy...~Dn, where > and ~ are the at least as likely as and as likely as relations between events, derived from betting preferences as in the class. Given any subsets N and N' of {1, 2. ....n}, show that UD UD - IN1 2 IN'. iEN iEN' (40 points) Consider the reduced normal form of the following game, in which the strategy set of Player 1 is {X, A, B}, so that the equivalent strategies X A and X B are represented by a single strategy X. X NO N 2 (a) Compute the set of rationalizable strategies. (Show your result.) (b) Compute the set correlated equilibria. (Show your result.) (c) Suppose that in addition to the type with the payoff function above, with proba- bility 0.1, Player 1 has a "crazy" type who gets 1 if he plays A and 0 otherwise. Compute the set of all sequential equilibria.Consider an economy with two types of individuals: skilled and unskilled workers. The only differ- ence between the two is that the skilled have a higher hourly wage w. = 40 than the unskilled do, wu = 10. Suppose that there are 400 unskilled and 100 skilled workers in this economy. Suppose that each individual has a utility function over consumption (c) and leisure (1) of the following form: U(c, 1) = In(c) + 2In(1) where I E [0, 24]. 1. (a) (3 minutes) Write down the individual's budget constraint in terms of consumption and leisure. Draw the budget constraints for the skilled and unskilled workers in the same graph with leisure on the r-axis. (b) (7 minutes) Solve for each individual's optimal leisure, labor, and consumption choice. 2. (10 minutes) Now suppose that the government wants to redistribute from the skilled to the unskilled workers. It levies an income tax which collects 20% of each skilled worker's earnings and then uses the tax revenue to give an equal amount (lump-sum transfer) T to each unskilled worker. So only the skilled workers are taxed and only the unskilled workers receive the transfer. (a) (4 minutes) On the same set of axes, draw the new budget constraints faced by the two types of individuals. (b) (4 minutes) Solve for each skilled individual's new optimal leisure, labor, and consump- tion. Does labor supply change? What is the intuition behind this result? (c) (2 minutes) Compute the total tax revenue collected by the government from taxing the skilled individuals. 3. (a) (4 minutes) Suppose that for every tax dollar collected, 6.25 cents are lost due to admin- istrative costs. Suppose that the government sets 7 so that it spends what it collects (the government balances its budget). How large is T"?\f