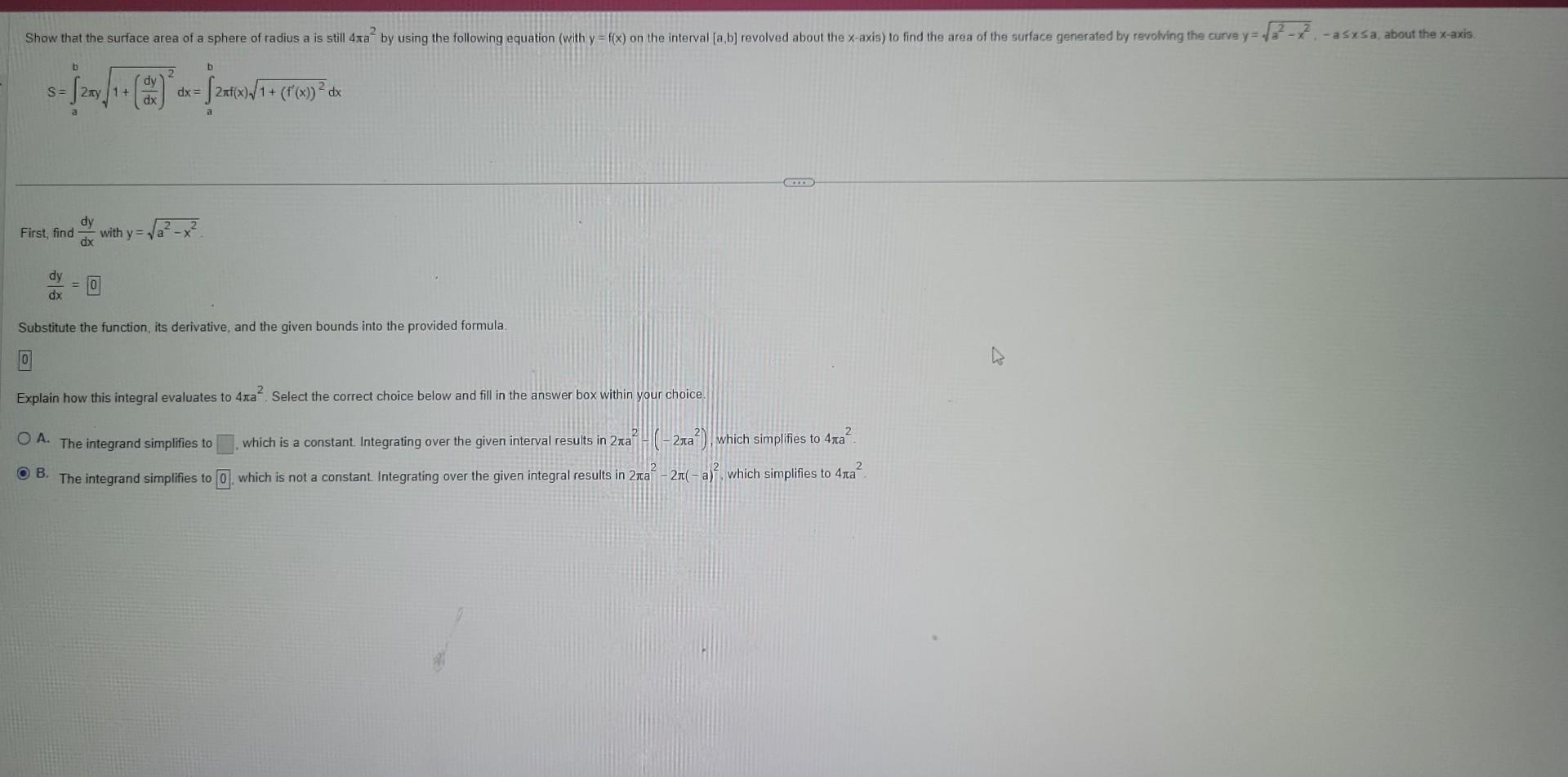
Show that the surface area of a sphere of radius a is still 4x by using the following equation (with y=f(x) on the interval [a,b] revolved about the x-axis) to find the area of the surface generated by revolving the curve y=-x-asxsa, about the x-axis. b dy s=[20/1 + (2) * S= dx First, find dy dx dy 0 b 1+ dx=2nf(x)/1+ (f'(x)) dx with y=a Substitute the function, its derivative, and the given bounds into the provided formula. Explain how this integral evaluates to 4xa. Select the correct choice below and fill in the answer box within your choice. 2 OA. The integrand simplifies to B. The integrand simplifies to [0] GEXE which is a constant. Integrating over the given interval results in 2ra-(-2ra), which simplifies to 4ra. which is not a constant. Integrating over the given integral results in 2ra - 2r(-a), which simplifies to 4ta 2