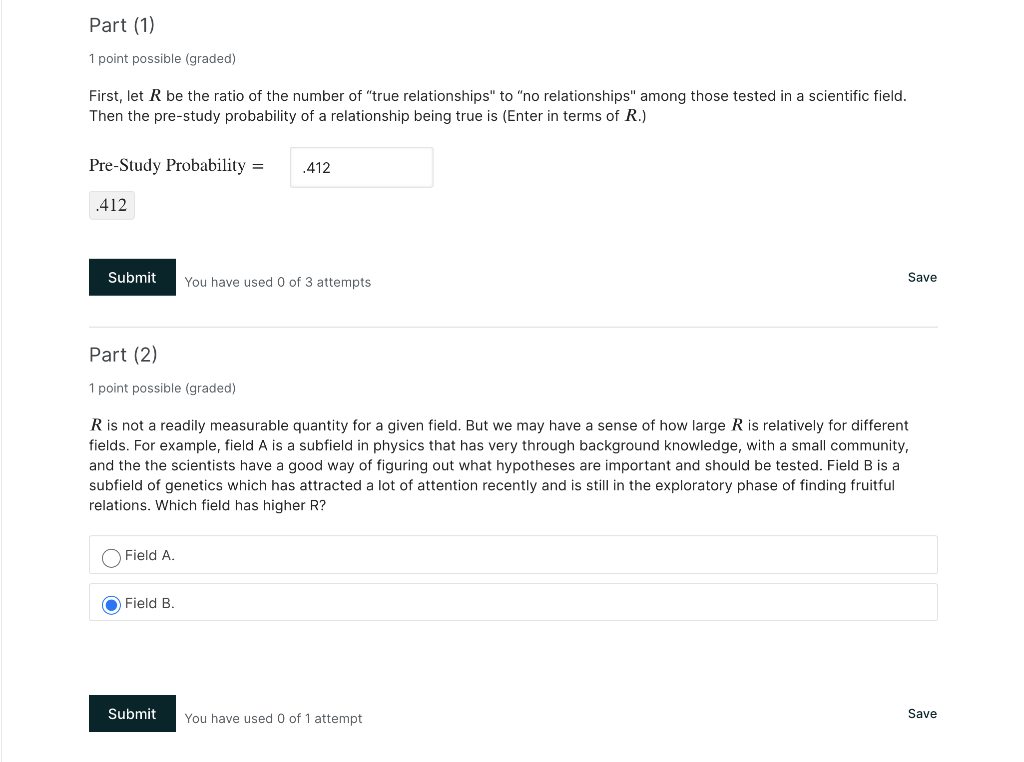
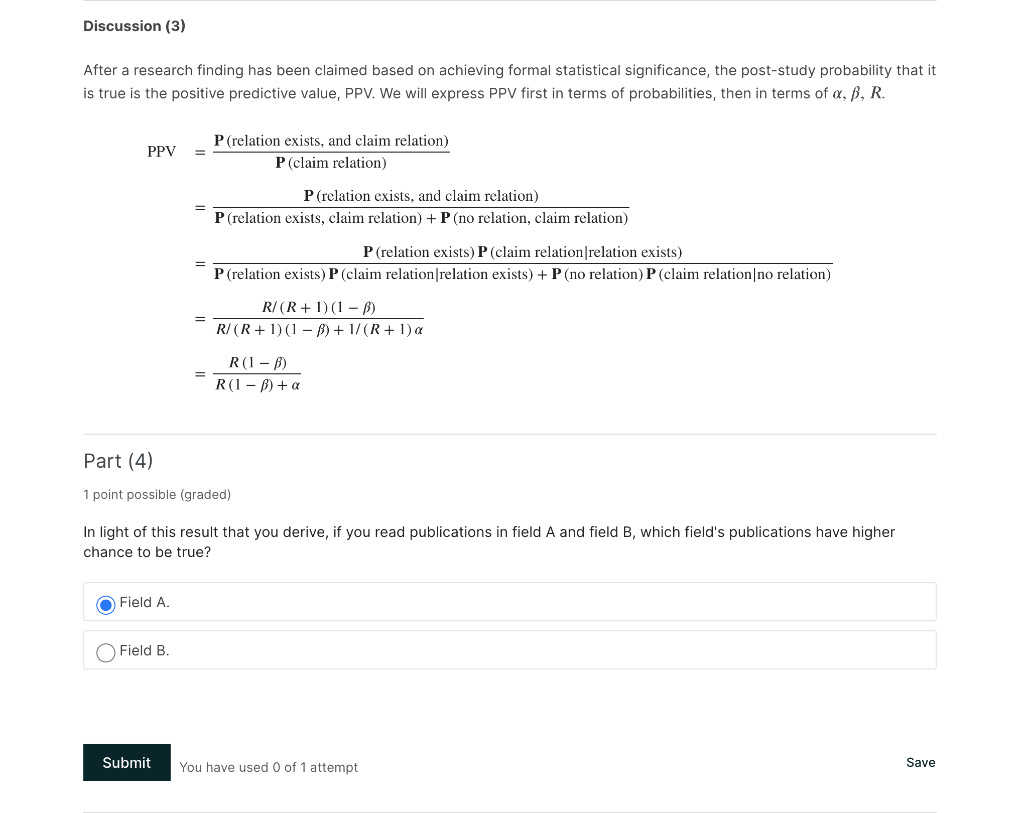
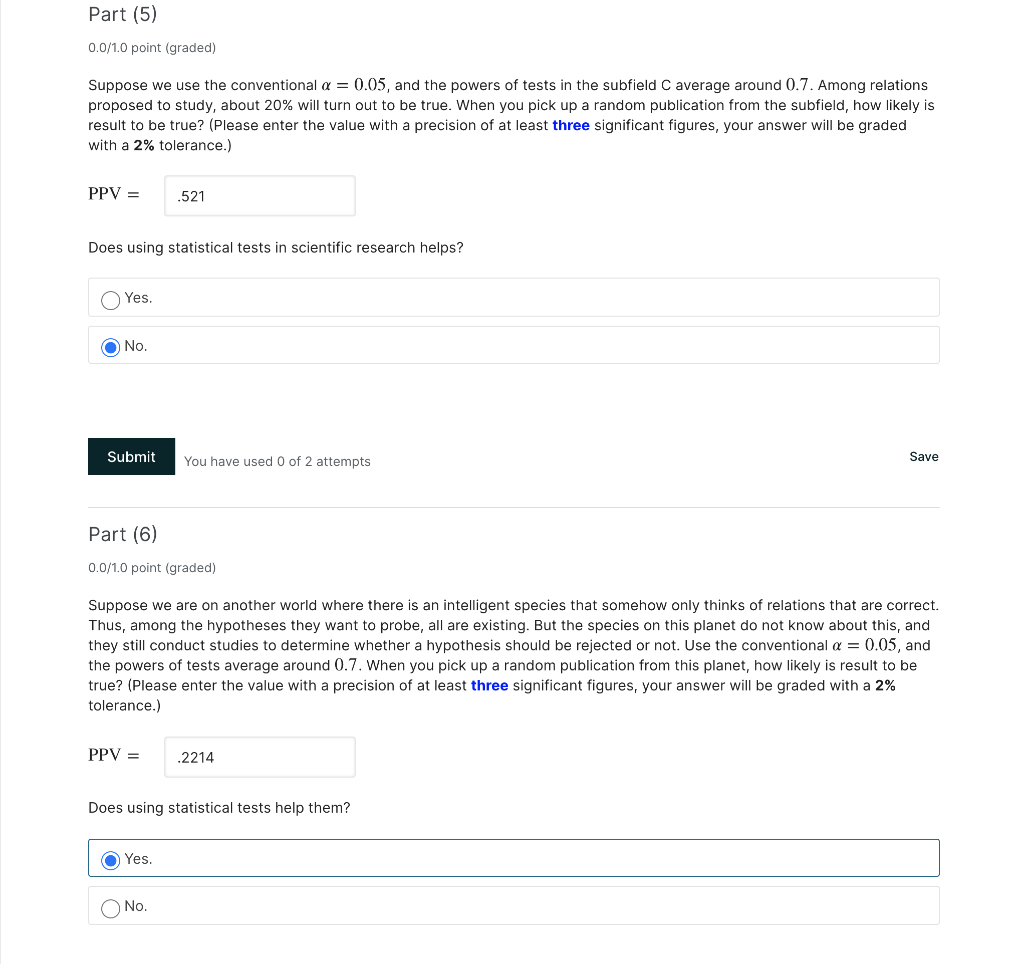
Read the paper by loannidis on why most published research findings are false (PLoS Medicine, 2005) and summarize the paper in your own words. What is the most important lesson you learned from reading this paper? How does loannidis get to the conclusion that a research finding is more likely true than false if (1 B) R > a (at the beginning of page 697)? What does this mean? Part (1) 1 point possible (graded) First, let R be the ratio of the number of "true relationships" to "no relationships" among those tested in a scientific field. Then the pre-study probability of a relationship being true is (Enter in terms of R.) Pre-Study Probability = .412 .412 Submit You have used 0 of 3 attempts Save Part (2) 1 point possible (graded) R is not a readily measurable quantity for a given field. But we may have a sense of how large R is relatively for different fields. For example, field A is a subfield in physics that has very through background knowledge, with a small community, and the the scientists have a good way of figuring out what hypotheses are important and should be tested. Field B is a subfield of genetics which has attracted a lot of attention recently and is still in the exploratory phase of finding fruitful relations. Which field has higher R? Field A. Field B. Submit You have used 0 of 1 attempt Save Discussion (3) After a research finding has been claimed based on achieving formal statistical significance, the post-study probability that it is true is the positive predictive value, PPV. We will express PPV first in terms of probabilities, then in terms of a, b, R. PPV P (relation exists, and claim relation) P (claim relation) P (relation exists, and claim relation) P (relation exists, claim relation) + P(no relation, claim relation) P (relation exists) P (claim relation relation exists) P (relation exists) P (claim relation relation exists) + P(no relation) P (claim relation|no relation) R/R + 1) (1 -B) R/(R+1) (1 B) + 1/(R+1) a R(1-B) R(1-B) + a Part (4) 1 point possible (graded) In light of this result that you derive, if you read publications in field A and field B, which field's publications have higher chance to be true? Field A. Field B. Submit You have used 0 of 1 attempt Save Part (5) 0.0/1.0 point (graded) Suppose we use the conventional a = 0.05, and the powers of tests in the subfield C average around 0.7. Among relations proposed to study, about 20% will turn out to be true. When you pick up a random publication from the subfield, how likely is result to be true? (Please enter the value with a precision of at least three significant figures, your answer will be graded with a 2% tolerance.) PPV = .521 Does using statistical tests in scientific research helps? Yes. No. Submit You have used 0 of 2 attempts Save Part (6) 0.0/1.0 point (graded) Suppose we are on another world where there is an intelligent species that somehow only thinks of relations that are correct. Thus, among the hypotheses they want to probe, all are existing. But the species on this planet do not know about this, and they still conduct studies to determine whether a hypothesis should be rejected or not. Use the conventional a = 0.05, and the powers of tests average around 0.7. When you pick up a random publication from this planet, how likely is result to be true? (Please enter the value with a precision of at least three significant figures, your answer will be graded with a 2% tolerance.) PPV = .2214 Does using statistical tests help them? Yes. No. Read the paper by loannidis on why most published research findings are false (PLoS Medicine, 2005) and summarize the paper in your own words. What is the most important lesson you learned from reading this paper? How does loannidis get to the conclusion that a research finding is more likely true than false if (1 B) R > a (at the beginning of page 697)? What does this mean? Part (1) 1 point possible (graded) First, let R be the ratio of the number of "true relationships" to "no relationships" among those tested in a scientific field. Then the pre-study probability of a relationship being true is (Enter in terms of R.) Pre-Study Probability = .412 .412 Submit You have used 0 of 3 attempts Save Part (2) 1 point possible (graded) R is not a readily measurable quantity for a given field. But we may have a sense of how large R is relatively for different fields. For example, field A is a subfield in physics that has very through background knowledge, with a small community, and the the scientists have a good way of figuring out what hypotheses are important and should be tested. Field B is a subfield of genetics which has attracted a lot of attention recently and is still in the exploratory phase of finding fruitful relations. Which field has higher R? Field A. Field B. Submit You have used 0 of 1 attempt Save Discussion (3) After a research finding has been claimed based on achieving formal statistical significance, the post-study probability that it is true is the positive predictive value, PPV. We will express PPV first in terms of probabilities, then in terms of a, b, R. PPV P (relation exists, and claim relation) P (claim relation) P (relation exists, and claim relation) P (relation exists, claim relation) + P(no relation, claim relation) P (relation exists) P (claim relation relation exists) P (relation exists) P (claim relation relation exists) + P(no relation) P (claim relation|no relation) R/R + 1) (1 -B) R/(R+1) (1 B) + 1/(R+1) a R(1-B) R(1-B) + a Part (4) 1 point possible (graded) In light of this result that you derive, if you read publications in field A and field B, which field's publications have higher chance to be true? Field A. Field B. Submit You have used 0 of 1 attempt Save Part (5) 0.0/1.0 point (graded) Suppose we use the conventional a = 0.05, and the powers of tests in the subfield C average around 0.7. Among relations proposed to study, about 20% will turn out to be true. When you pick up a random publication from the subfield, how likely is result to be true? (Please enter the value with a precision of at least three significant figures, your answer will be graded with a 2% tolerance.) PPV = .521 Does using statistical tests in scientific research helps? Yes. No. Submit You have used 0 of 2 attempts Save Part (6) 0.0/1.0 point (graded) Suppose we are on another world where there is an intelligent species that somehow only thinks of relations that are correct. Thus, among the hypotheses they want to probe, all are existing. But the species on this planet do not know about this, and they still conduct studies to determine whether a hypothesis should be rejected or not. Use the conventional a = 0.05, and the powers of tests average around 0.7. When you pick up a random publication from this planet, how likely is result to be true? (Please enter the value with a precision of at least three significant figures, your answer will be graded with a 2% tolerance.) PPV = .2214 Does using statistical tests help them? Yes. No