read this :

then answer this question

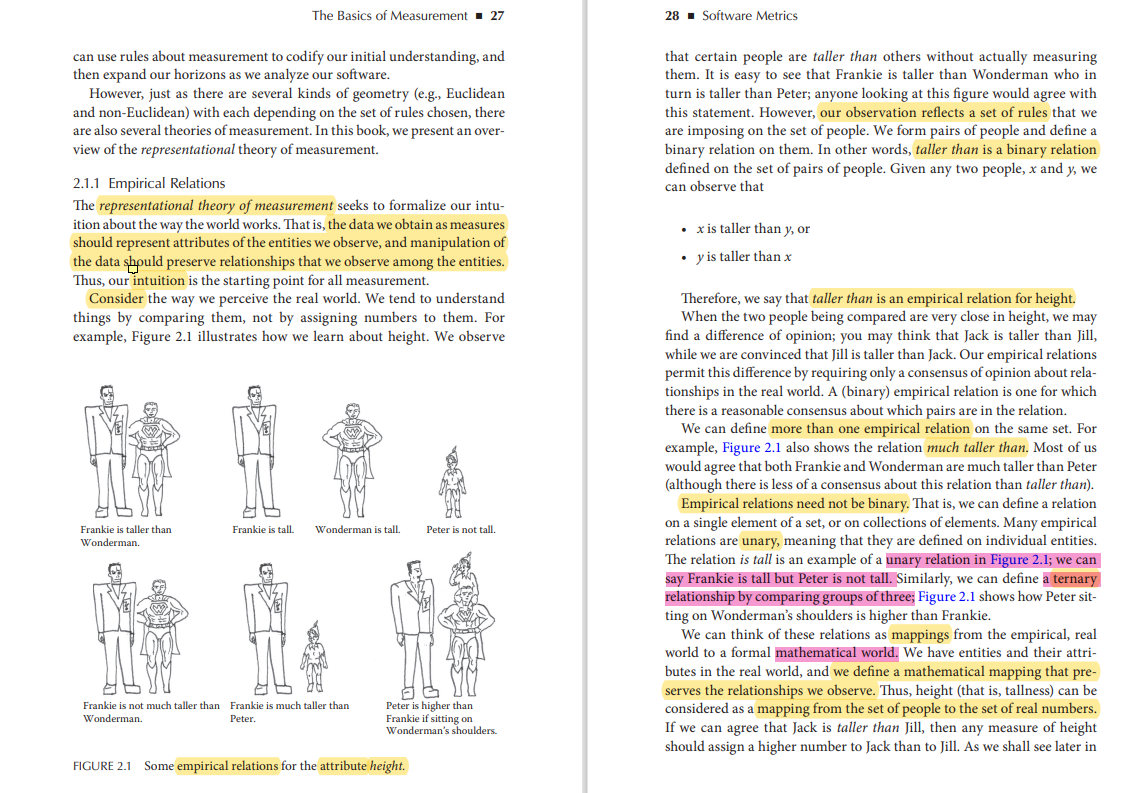
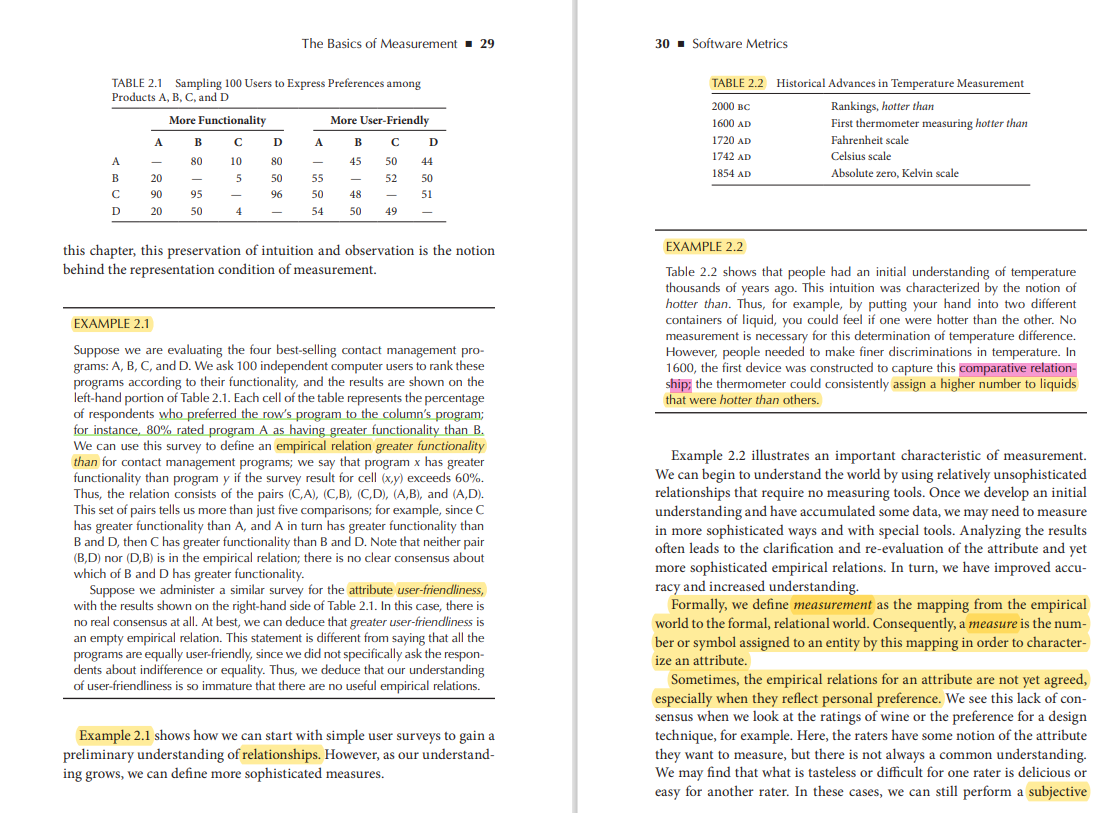
The Basics of Measurement - 27 28 - Software Metrics can use rules about measurement to codify our initial understanding, and then expand our horizons as we analyze our software. However, just as there are several kinds of geometry (e.g., Euclidean and non-Euclidean) with each depending on the set of rules chosen, there are also several theories of measurement. In this book, we present an over- view of the representational theory of measurement. that certain people are taller than others without actually measuring them. It is easy to see that Frankie is taller than Wonderman who in turn is taller than Peter; anyone looking at this figure would agree with this statement. However, our observation reflects a set of rules that we are imposing on the set of people. We form pairs of people and define a binary relation on them. In other words, taller than is a binary relation defined on the set of pairs of people. Given any two people, x and y, we can observe that 2.1.1 Empirical Relations The representational theory of measurement seeks to formalize our intu- ition about the way the world works. That is, the data we obtain as measures should represent attributes of the entities we observe, and manipulation of the data should preserve relationships that we observe among the entities. Thus, our intuition is the starting point for all measurement. Consider the way we perceive the real world. We tend to understand things by comparing them, not by assigning numbers to them. For example, Figure 2.1 illustrates how we learn about height. We observe x is taller than y, or y is taller than x Frankie is tall. Wonderman is tall. Therefore, we say that taller than is an empirical relation for height. When the two people being compared are very close in height, we may find a difference of opinion; you may think that Jack is taller than Jill, while we are convinced that Jill is taller than Jack. Our empirical relations permit this difference by requiring only a consensus of opinion about rela- tionships in the real world. A (binary) empirical relation is one for which there is a reasonable consensus about which pairs are in the relation. We can define more than one empirical relation on the same set. For example, Figure 2.1 also shows the relation much taller than. Most of us would agree that both Frankie and Wonderman are much taller than Peter (although there is less of a consensus about this relation than taller than). Empirical relations need not be binary. That is, we can define a relation on a single element of a set, or on collections of elements. Many empirical relations are unary, meaning that they are defined on individual entities. The relation is tall is an example of a unary relation in Figure 2.1; we can say Frankie is tall but Peter is not tall. Similarly, we can define a ternary relationship by comparing groups of three; Figure 2.1 shows how Peter sit- ting on Wonderman's shoulders is higher than Frankie. We can think of these relations as mappings from the empirical, real world to a formal mathematical world. We have entities and their attri- butes in the real world, and we define a mathematical mapping that pre- serves the relationships we observe. Thus, height (that is, tallness) can be considered as a mapping from the set of people to the set of real numbers. If we can agree that Jack is taller than Jill, then any measure of height should assign a higher number to Jack than to Jill. As we shall see later in Peter is not tall. Frankie is taller than Wonderman Frankie is not much taller than Frankie is much taller than Wonderman Peter. Peter is higher than Frankie if sitting on Wonderman's shoulders. FIGURE 2.1 Some empirical relations for the attribute height. The Basics of Measurement 29 30 - Software Metrics TABLE 2.1 Sampling 100 Users to Express Preferences among Products A, B, C, and D More Functionality More User-Friendly TABLE 2.2 Historical Advances in Temperature Measurement 2000 BC Rankings, hotter than 1600 AD First thermometer measuring hotter than 1720 AD Fahrenheit scale 1742 AD Celsius scale 1854 AD Absolute zero, Kelvin scale A B D A D B 45 80 50 A B 10 5 80 50 96 20 90 20 52 44 50 51 55 50 54 95 48 50 D 50 4 49 EXAMPLE 2.2 this chapter, this preservation of intuition and observation is the notion behind the representation condition of measurement. Table 2.2 shows that people had an initial understanding of temperature thousands of years ago. This intuition was characterized by the notion of hotter than. Thus, for example, by putting your hand into two different containers of liquid, you could feel if one were hotter than the other. No measurement is necessary for this determination of temperature difference. However, people needed to make finer discriminations in temperature. In 1600, the first device was constructed to capture this comparative relation- ship; the thermometer could consistently assign a higher number to liquids that were hotter than others. EXAMPLE 2.1 Suppose we are evaluating the four best-selling contact management pro- grams: A, B, C, and D. We ask 100 independent computer users to rank these programs according to their functionality, and the results are shown on the left-hand portion of Table 2.1. Each cell of the table represents the p percentage of respondents who preferred the row's program to the column's program for instance, 80% rated program A as having greater functionality than B. We can use this survey to define an empirical relation greater functionality than for contact management programs; we say program x has greater functionality than program y if the survey result for cell (x,y) exceeds 60%. Thus, the relation consists of the pairs (CA), (C,B),(CD), (A,B), and (A,D). This set of pairs tells us more than e comparisons; for has greater functionality than A, and A in turn has greater functionality than B and D, then C has greater functionality than B and D. Note that neither pair (B,D) nor (D,B) is in the empirical relation, there is no clear consensus about D) which of B and D has greater functionality. Suppose we a similar surv survey for the attribute user-friendliness, with the results shown on the right-hand side of Table 2.1. In this case, there no real consensus at all. At best, we can deduce that greater user-friendliness is an empty empirical relation. This statement is different from saying that all the programs are equally user-friendly, since we did not specifically ask the respon- dents about indifference or equality. Thus, we deduce that our understanding of user-friendliness is so immature that there are no useful empirical relations. just five example, since pose we administer a is Example 2.2 illustrates an important characteristic of measurement. We can begin to understand the world by using relatively unsophisticated relationships that require no measuring tools. Once we develop an initial understanding and have accumulated some data, we may need to measure in more sophisticated ways and with special tools. Analyzing the results often leads to the clarification and re-evaluation of the attribute and yet more sophisticated empirical relations. In turn, we have improved accu- racy and increased understanding. Formally, we define measurement as the mapping from the empirical world to the formal, relational world. Consequently, a measure is the num- ber or symbol assigned to an entity by this mapping in order to character- ize an attribute. Sometimes, the empirical relations for an attribute are not yet agreed, especially when they reflect personal preference. We see this lack of con- sensus when we look at the ratings of wine or the preference for a design technique, for example. Here, the raters have some notion of the attribute they want to measure, but there is not always a common understanding. We may find that what is tasteless or difficult for one rater is delicious or easy for another rater. In these cases, we can still perform a subjective Example 2.1 shows how we can start with simple user surveys to gain a preliminary understanding of relationships. However, as our understand- ing grows, we can define more sophisticated measures. 32 . Software Metrics The Basics of Measurement 33 their assumptions are therefore different, and the resulting number is differ- ent. For this reason, we must make the mapping rules explicit assessment, but the result is not necessarily a measure, in the sense of measurement theory. For example, Figure 2.2 shows several rating for- mats, some of which you may have encountered in taking examinations or opinion polls. These questionnaires capture useful data. They enable us to establish the basis for empirical relations, characterizing properties so that formal measurement may be possible in the future. 2.1.2 The Rules of the Mapping We have seen how a measure is used to characterize an attribute. We begin in the real world, studying an entity and trying to understand more about it. Thus, the real world is the domain of the mapping, and the mathemati- cal world is the range. When we map the attribute to a mathematical sys- tem, we have many choices for the mapping and the range. We can use real numbers, integers, or even a set of non-numeric symbols. We encounter some of the same problems in measuring software. For example, many organizations measure the size of their source code in terms of the number of lines of code (LOC) in a program. But the defini- tion of a line of code must be made clear. The US Software Engineering Institute developed a checklist to assist developers in deciding exactly what is included in a line of code (Park 1992). This standard is still used by major organizations and metrics tool providers (see, e.g., the unified code counter tool produced by University of Southern California in collaboration with the Aerospace Corporation (Pfeiffer, 2012). Figure 2.3 illustrates part of the checklist, showing how different choices result in different counting rules. Thus, the checklist allows you to tailor your definition of lines-of-code to your needs. We will examine the issues addressed by this checklist in more depth in Chapter 8. Many systems consist of programs in a variety of languages. For exam- ple, the GNU/Linux distribution includes code written in at least 19 differ- ent languages (Wheeler 2002). In order to deal with code written in such a variety of languages, David Wheeler's code analysis tool uses a simple scheme for counting LOC: a physical source line of code is a line ending in a newline or end-of-file marker, and which contains at least one non- whitespace non-comment character." EXAMPLE 2.3 To measure a person's height, it is not enough to simply specify a number. If we measure height in inches, then we are defining a mapping from the set of people into inches; if we measure height in centimeters, then we have a different mapping. Moreover, even when the domain and range are the same, the mapping definition may be different. That is, there may be many different mappings (and hence different ways of measuring) depending on the conven- tions we adopt. For example, we may or may not allow shoes to be worn, or we may measure people standing or sitting. Thus, a measure must specify the domain and range as well as the rule for performing the mapping. EXAMPLE 2.4 In some everyday situations, a measure is associated with a number, the assumptions about the mapping are well known, and our terminology is imprecise. For example, we say "Felix's age is 11," or "Felix is 11." In expressing ourselves in this way, we really mean that we are measuring age by mapping each person into years in such a way that we count only whole years since birth. But there are many different rules that we can use. For example, the Chinese measure age by counting from the time of conception; 2.1.3 The Representation Condition of Measurement We saw that, by definition, each relation in the empirical relational system corresponds via the measurement to an element in a number system. We want the properties of the measures in the number system to be the same as the corresponding elements in the real world, so that by studying the numbers, we learn about the real world. Thus, we want the mapping to preserve the relation. This rule is called the representation condition, and it is illustrated in Figure 2.4. The representation condition asserts that a measurement mapping Mmust map entities into numbers and empirical relations into numerical relations in such a way that the empirical relations preserve and are preserved by the numerical relations. In Figure 2.4, we see that the empirical relation taller than is mapped to the numerical relation >. In particular, we can say that A is taller than B if and only if M(A) > M(B) The Basics of Measurement 35 Real world Number system M Joe i Fred 63 72 Joe taller than Fred M(Joe) > M(Fred) Empirical relation Preserved under Mas Numerical relation FIGURE 2.4 Representation condition. This statement means that: Whenever Joe is taller than Fred, then M(Joe) must be a bigger num- ber than M(Fred). We can map Jill to a higher number than Jack only if Jill is taller than Jack. a EXAMPLE 2.5 In Section 2.1.1, we noted that there can be many relations on a given set, and we mentioned several for the attribute height. The representa- tion condition has implications for each of these relations. Consider these examples: For the (binary) empirical relation taller than, we can have the numerical relation x> Then, the representation condition requires that for any measure M, A taller than B if and only if M(A)> M(B) For the (unary) empirical relation is-tall, we might have the numerical relation x > 70 The representation condition requires that for any measure M, A is-tall if and only if M(A) > 70 abs Question 5: Lab 2: Entities, Attributes, Relationships and Mappings Activity: Reading Exercise (p-27 to 35. P-31 & 34 are not included). This text describes the theory of measurement especially the concepts of entities, attributes, relationships, and mapping, What are the entities described in the above figure? Question 6: Task: The following figure describes three persons F, W and P and their heights 84, 72, and 42 respectively. 6.1- Write one unary empirical relation relative to above figure? 6.2- Why it is unary? ? Question 7: 7.1- Write one binary empirical relation relative to above figure? 7.2- Why it is binary? Question 8: 8.1- Write one possible ternary empirical relation in this figure? M M 84 72 42 8.2- Why it is ternary relation? Question 9: Statement: "If the person in the above figure have height greater than 80, they would be considered tall." 9.1- Based on the above statement, if the height of F is greater than 80 then how we can write it in the form of unary numerical relation? 9.2- and what would be the representation condition? Question 10: F w P Question 1: 1: In the above figure if we say that "F is taller than W", how we can write that in numerical relation? Question 2: Statement: "If the height of anyone in the above figure is more than 20cm than the others the first person would be considered much toller than." Write "F is taller than W" as mapping? Question 3: 3 How "taller than" can be written in numerical relation? Question 4: If we say that the height of Wis 20cm more than the height of P. Then what would be the representation condition for that? What attribute we are measuring? The Basics of Measurement - 27 28 - Software Metrics can use rules about measurement to codify our initial understanding, and then expand our horizons as we analyze our software. However, just as there are several kinds of geometry (e.g., Euclidean and non-Euclidean) with each depending on the set of rules chosen, there are also several theories of measurement. In this book, we present an over- view of the representational theory of measurement. that certain people are taller than others without actually measuring them. It is easy to see that Frankie is taller than Wonderman who in turn is taller than Peter; anyone looking at this figure would agree with this statement. However, our observation reflects a set of rules that we are imposing on the set of people. We form pairs of people and define a binary relation on them. In other words, taller than is a binary relation defined on the set of pairs of people. Given any two people, x and y, we can observe that 2.1.1 Empirical Relations The representational theory of measurement seeks to formalize our intu- ition about the way the world works. That is, the data we obtain as measures should represent attributes of the entities we observe, and manipulation of the data should preserve relationships that we observe among the entities. Thus, our intuition is the starting point for all measurement. Consider the way we perceive the real world. We tend to understand things by comparing them, not by assigning numbers to them. For example, Figure 2.1 illustrates how we learn about height. We observe x is taller than y, or y is taller than x Frankie is tall. Wonderman is tall. Therefore, we say that taller than is an empirical relation for height. When the two people being compared are very close in height, we may find a difference of opinion; you may think that Jack is taller than Jill, while we are convinced that Jill is taller than Jack. Our empirical relations permit this difference by requiring only a consensus of opinion about rela- tionships in the real world. A (binary) empirical relation is one for which there is a reasonable consensus about which pairs are in the relation. We can define more than one empirical relation on the same set. For example, Figure 2.1 also shows the relation much taller than. Most of us would agree that both Frankie and Wonderman are much taller than Peter (although there is less of a consensus about this relation than taller than). Empirical relations need not be binary. That is, we can define a relation on a single element of a set, or on collections of elements. Many empirical relations are unary, meaning that they are defined on individual entities. The relation is tall is an example of a unary relation in Figure 2.1; we can say Frankie is tall but Peter is not tall. Similarly, we can define a ternary relationship by comparing groups of three; Figure 2.1 shows how Peter sit- ting on Wonderman's shoulders is higher than Frankie. We can think of these relations as mappings from the empirical, real world to a formal mathematical world. We have entities and their attri- butes in the real world, and we define a mathematical mapping that pre- serves the relationships we observe. Thus, height (that is, tallness) can be considered as a mapping from the set of people to the set of real numbers. If we can agree that Jack is taller than Jill, then any measure of height should assign a higher number to Jack than to Jill. As we shall see later in Peter is not tall. Frankie is taller than Wonderman Frankie is not much taller than Frankie is much taller than Wonderman Peter. Peter is higher than Frankie if sitting on Wonderman's shoulders. FIGURE 2.1 Some empirical relations for the attribute height. The Basics of Measurement 29 30 - Software Metrics TABLE 2.1 Sampling 100 Users to Express Preferences among Products A, B, C, and D More Functionality More User-Friendly TABLE 2.2 Historical Advances in Temperature Measurement 2000 BC Rankings, hotter than 1600 AD First thermometer measuring hotter than 1720 AD Fahrenheit scale 1742 AD Celsius scale 1854 AD Absolute zero, Kelvin scale A B D A D B 45 80 50 A B 10 5 80 50 96 20 90 20 52 44 50 51 55 50 54 95 48 50 D 50 4 49 EXAMPLE 2.2 this chapter, this preservation of intuition and observation is the notion behind the representation condition of measurement. Table 2.2 shows that people had an initial understanding of temperature thousands of years ago. This intuition was characterized by the notion of hotter than. Thus, for example, by putting your hand into two different containers of liquid, you could feel if one were hotter than the other. No measurement is necessary for this determination of temperature difference. However, people needed to make finer discriminations in temperature. In 1600, the first device was constructed to capture this comparative relation- ship; the thermometer could consistently assign a higher number to liquids that were hotter than others. EXAMPLE 2.1 Suppose we are evaluating the four best-selling contact management pro- grams: A, B, C, and D. We ask 100 independent computer users to rank these programs according to their functionality, and the results are shown on the left-hand portion of Table 2.1. Each cell of the table represents the p percentage of respondents who preferred the row's program to the column's program for instance, 80% rated program A as having greater functionality than B. We can use this survey to define an empirical relation greater functionality than for contact management programs; we say program x has greater functionality than program y if the survey result for cell (x,y) exceeds 60%. Thus, the relation consists of the pairs (CA), (C,B),(CD), (A,B), and (A,D). This set of pairs tells us more than e comparisons; for has greater functionality than A, and A in turn has greater functionality than B and D, then C has greater functionality than B and D. Note that neither pair (B,D) nor (D,B) is in the empirical relation, there is no clear consensus about D) which of B and D has greater functionality. Suppose we a similar surv survey for the attribute user-friendliness, with the results shown on the right-hand side of Table 2.1. In this case, there no real consensus at all. At best, we can deduce that greater user-friendliness is an empty empirical relation. This statement is different from saying that all the programs are equally user-friendly, since we did not specifically ask the respon- dents about indifference or equality. Thus, we deduce that our understanding of user-friendliness is so immature that there are no useful empirical relations. just five example, since pose we administer a is Example 2.2 illustrates an important characteristic of measurement. We can begin to understand the world by using relatively unsophisticated relationships that require no measuring tools. Once we develop an initial understanding and have accumulated some data, we may need to measure in more sophisticated ways and with special tools. Analyzing the results often leads to the clarification and re-evaluation of the attribute and yet more sophisticated empirical relations. In turn, we have improved accu- racy and increased understanding. Formally, we define measurement as the mapping from the empirical world to the formal, relational world. Consequently, a measure is the num- ber or symbol assigned to an entity by this mapping in order to character- ize an attribute. Sometimes, the empirical relations for an attribute are not yet agreed, especially when they reflect personal preference. We see this lack of con- sensus when we look at the ratings of wine or the preference for a design technique, for example. Here, the raters have some notion of the attribute they want to measure, but there is not always a common understanding. We may find that what is tasteless or difficult for one rater is delicious or easy for another rater. In these cases, we can still perform a subjective Example 2.1 shows how we can start with simple user surveys to gain a preliminary understanding of relationships. However, as our understand- ing grows, we can define more sophisticated measures. 32 . Software Metrics The Basics of Measurement 33 their assumptions are therefore different, and the resulting number is differ- ent. For this reason, we must make the mapping rules explicit assessment, but the result is not necessarily a measure, in the sense of measurement theory. For example, Figure 2.2 shows several rating for- mats, some of which you may have encountered in taking examinations or opinion polls. These questionnaires capture useful data. They enable us to establish the basis for empirical relations, characterizing properties so that formal measurement may be possible in the future. 2.1.2 The Rules of the Mapping We have seen how a measure is used to characterize an attribute. We begin in the real world, studying an entity and trying to understand more about it. Thus, the real world is the domain of the mapping, and the mathemati- cal world is the range. When we map the attribute to a mathematical sys- tem, we have many choices for the mapping and the range. We can use real numbers, integers, or even a set of non-numeric symbols. We encounter some of the same problems in measuring software. For example, many organizations measure the size of their source code in terms of the number of lines of code (LOC) in a program. But the defini- tion of a line of code must be made clear. The US Software Engineering Institute developed a checklist to assist developers in deciding exactly what is included in a line of code (Park 1992). This standard is still used by major organizations and metrics tool providers (see, e.g., the unified code counter tool produced by University of Southern California in collaboration with the Aerospace Corporation (Pfeiffer, 2012). Figure 2.3 illustrates part of the checklist, showing how different choices result in different counting rules. Thus, the checklist allows you to tailor your definition of lines-of-code to your needs. We will examine the issues addressed by this checklist in more depth in Chapter 8. Many systems consist of programs in a variety of languages. For exam- ple, the GNU/Linux distribution includes code written in at least 19 differ- ent languages (Wheeler 2002). In order to deal with code written in such a variety of languages, David Wheeler's code analysis tool uses a simple scheme for counting LOC: a physical source line of code is a line ending in a newline or end-of-file marker, and which contains at least one non- whitespace non-comment character." EXAMPLE 2.3 To measure a person's height, it is not enough to simply specify a number. If we measure height in inches, then we are defining a mapping from the set of people into inches; if we measure height in centimeters, then we have a different mapping. Moreover, even when the domain and range are the same, the mapping definition may be different. That is, there may be many different mappings (and hence different ways of measuring) depending on the conven- tions we adopt. For example, we may or may not allow shoes to be worn, or we may measure people standing or sitting. Thus, a measure must specify the domain and range as well as the rule for performing the mapping. EXAMPLE 2.4 In some everyday situations, a measure is associated with a number, the assumptions about the mapping are well known, and our terminology is imprecise. For example, we say "Felix's age is 11," or "Felix is 11." In expressing ourselves in this way, we really mean that we are measuring age by mapping each person into years in such a way that we count only whole years since birth. But there are many different rules that we can use. For example, the Chinese measure age by counting from the time of conception; 2.1.3 The Representation Condition of Measurement We saw that, by definition, each relation in the empirical relational system corresponds via the measurement to an element in a number system. We want the properties of the measures in the number system to be the same as the corresponding elements in the real world, so that by studying the numbers, we learn about the real world. Thus, we want the mapping to preserve the relation. This rule is called the representation condition, and it is illustrated in Figure 2.4. The representation condition asserts that a measurement mapping Mmust map entities into numbers and empirical relations into numerical relations in such a way that the empirical relations preserve and are preserved by the numerical relations. In Figure 2.4, we see that the empirical relation taller than is mapped to the numerical relation >. In particular, we can say that A is taller than B if and only if M(A) > M(B) The Basics of Measurement 35 Real world Number system M Joe i Fred 63 72 Joe taller than Fred M(Joe) > M(Fred) Empirical relation Preserved under Mas Numerical relation FIGURE 2.4 Representation condition. This statement means that: Whenever Joe is taller than Fred, then M(Joe) must be a bigger num- ber than M(Fred). We can map Jill to a higher number than Jack only if Jill is taller than Jack. a EXAMPLE 2.5 In Section 2.1.1, we noted that there can be many relations on a given set, and we mentioned several for the attribute height. The representa- tion condition has implications for each of these relations. Consider these examples: For the (binary) empirical relation taller than, we can have the numerical relation x> Then, the representation condition requires that for any measure M, A taller than B if and only if M(A)> M(B) For the (unary) empirical relation is-tall, we might have the numerical relation x > 70 The representation condition requires that for any measure M, A is-tall if and only if M(A) > 70 abs Question 5: Lab 2: Entities, Attributes, Relationships and Mappings Activity: Reading Exercise (p-27 to 35. P-31 & 34 are not included). This text describes the theory of measurement especially the concepts of entities, attributes, relationships, and mapping, What are the entities described in the above figure? Question 6: Task: The following figure describes three persons F, W and P and their heights 84, 72, and 42 respectively. 6.1- Write one unary empirical relation relative to above figure? 6.2- Why it is unary? ? Question 7: 7.1- Write one binary empirical relation relative to above figure? 7.2- Why it is binary? Question 8: 8.1- Write one possible ternary empirical relation in this figure? M M 84 72 42 8.2- Why it is ternary relation? Question 9: Statement: "If the person in the above figure have height greater than 80, they would be considered tall." 9.1- Based on the above statement, if the height of F is greater than 80 then how we can write it in the form of unary numerical relation? 9.2- and what would be the representation condition? Question 10: F w P Question 1: 1: In the above figure if we say that "F is taller than W", how we can write that in numerical relation? Question 2: Statement: "If the height of anyone in the above figure is more than 20cm than the others the first person would be considered much toller than." Write "F is taller than W" as mapping? Question 3: 3 How "taller than" can be written in numerical relation? Question 4: If we say that the height of Wis 20cm more than the height of P. Then what would be the representation condition for that? What attribute we are measuring