Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Recall we define SXT = {(s, t): sS and t T}. For each of the following, prove it if it is always true, else
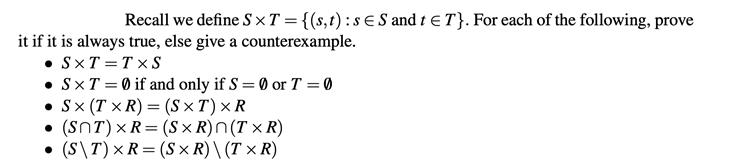
Recall we define SXT = {(s, t): sS and t T}. For each of the following, prove it if it is always true, else give a counterexample. SXT=TXS SXT = 0 if and only if S = 0 or T = 0 Sx (TxR) = (SxT) XR (SNT) XR=(SXR)n(TXR) (S\T) XR=(SXR)\ (TxR)
Step by Step Solution
★★★★★
3.41 Rating (151 Votes )
There are 3 Steps involved in it
Step: 1
Answer To prove or disprove the statements lets define sets S T and R and examine each case separately 1 SXT TXS To prove this statement we need to show that for any sets S and T the set SXT is equal ...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
An Introduction to Analysis
Authors: William R. Wade
4th edition
132296381, 978-0132296380
