Receiving many wrong answers from chegg experts. May I get the correct answers?

Your goal for this breakout is to create an easy-to-use Matrix class in C++ that makes use of dynamic memory allocation and includes basic matrix operations both in the form of regular functions and via operator overloading.

Here is the basic prototype for the Matrix class (you may need to add more to it to support some of the additional features listed further down in this document):

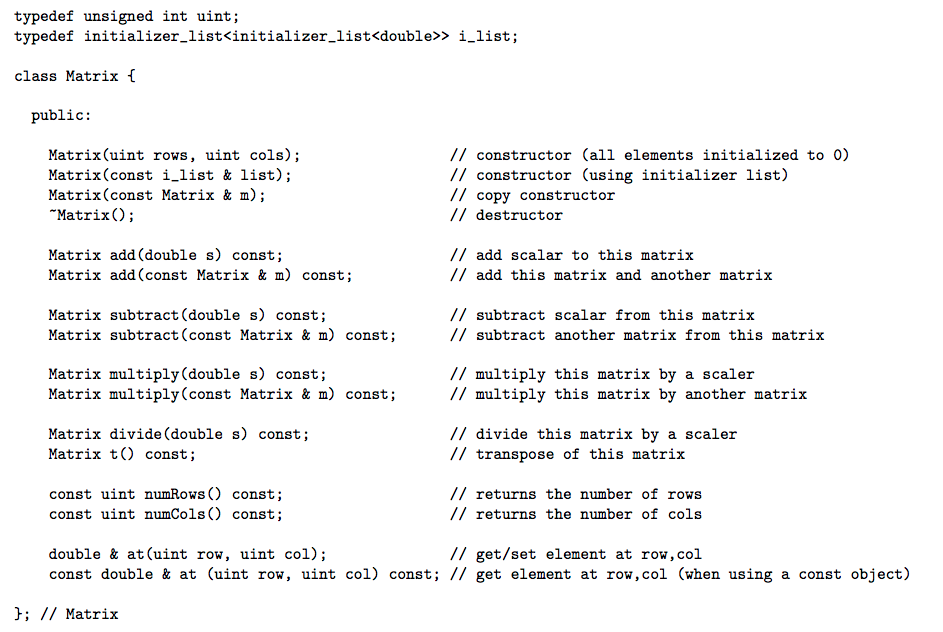
Important Class Details

Your Matrix implementation will contain elements of type double. In the prototype presented above, the term scaler refers to a regular number. For example, if you add a scaler to a matrix, then each element in the matrix gets that number added to it. Contrast this with the member functions that take a Matrix as their parameter. These functions represent regular matrix operations. For some of these operations (e.g., multiplication, transpose, etc.), you may need to consult some sort of reference in order to recall the exact procedure/meaning behind the operation.

NOTE: You MAY assume valid input for all operations. NOTE: You MAY NOT use library classes such as std::array, std::vector, std::list, etc. for this project. You must

implement your Matrix class internally using a dynamically allocated array.

Example Usage 1

Matrix a(2, 2); a.at(0, 0) = 1; // [ 1, 2 ] a.at(0, 1) = 2; // [ 1, 3 ] a.at(1, 0) = 1; a.at(1, 1) = 3; 

Matrix b(2, 1); b.at(0, 0) = 3; // [ 3 ] b.at(1, 0) = 2; // [ 2 ] 

Matrix c = a.multiply(b); cout

  
Matrix d = {{1, 2}, // this will implicitly call the overloaded constructor {3, 4}}; // that takes an initializer list 
 
The usage of the member function at(uint, uint) is what facilities our ability to perform operations such as a.at(0, 0) = 1. If you implement this function carefully, then this behavior should work because the function returns a reference to an element. In order to support the constructor overload (i.e., matrix construction using an initializer list), you will need to use a standard template library (STL) class called std::initializer list1. The type signature for the  or simply i list if you use the provided typedef
 
Operator Overloading
 
You will also need to overload operators in order to support the following functionality. It is up to you whether or not these should be member or non-member overloads.
 
// assume we have two matrices of appropriate size already set up Matrix a; Matrix b; 
 
// after providing the overloads, you should be able to do any of the following operations // using regular operators instead of the member functions Matrix c0 = a + 5.2; Matrix c1 = a + a; // NOTE: these examples actually end up calling the copy constructor Matrix c2 = a - 3.5; // e.g., this line is the same as Matrix c2(a - 3.5); 
 
Matrix c3 = b - b; Matrix c4 = a * 2.1; Matrix c5 = a * b; Matrix c6 = a / 2.0; 
 
You should also support stream insertion (similar to overriding the toString method in Java) so that your matrices can easily be printed.
 
cout  
You should also support matrix assignment using an initializer list (to easily overwrite existing elements) that looks like the following:
 
Matrix d(2, 2); d = {{ 1, 2 }, 
 
{ 3, 4 }};
 
In order to support this last operator overload (i.e., matrix assignment using an initializer list), you will need to use a standard template library (STL) class called std::initializer list. The type signature for the  or simply i list if you use the provided typedef. It is preferred that you specify the parameter as a const i list & in order to avoid any unnecessary copying.
 
Additional Features
 
In addition to the requirements for listed above, you need to make sure your Matrix class supports the following features:
 
 Overloaded Function Call Operator (operator()(uint row, uint col)): After creating a (non-dynamically allocated) Matrix object, the user should be able to access the elements using the function call operator (as an alternative to using the at function):
 
 Matrix a(1, 1); a(0, 0) = 5; cout  
 Overloaded Copy Assignment Operator (operator=(const Matrix &)): You should have already overloaded the assignment operator to take in a special kind of initializer list. Now you need to provide an additional overload that supports copy assignment. This will make your Matrix class more consistent since copy assignment parallels copy construction. Here is an example:
 
 Matrix a(1, 1); a(0, 0) = 5; 
 
 Matrix b(1, 1); b = a; // copy assignment 
 
 Overloaded Non-Member Arithmetic Operators for Scalers: You should have already created overloads to support the basic arithmetic operations where the right-hand-side of an operation is a scaler value. Now you need to implement operator overloads so that scalers can be used on the left-hand-side of an operation. Here is an example showing the operators that you need to support:
 
 Matrix a = {{1, 2}, {3, 4}}; 
 
 Matrix b = 4.0 + a; // [ 5, 6 ] // [ 7, 8 ] 
 
 Matrix c = 4.0 - a; // [ 3, 2 ] // [ 1, 0 ] 
 
 Matrix d = 2.0 * a; // [ 2, 4 ] // [ 6, 8 ] 
 
 Matrix e = 12.0 / a; // [ 12, 6 ] [ 4, 3 ] 
 
 Overloaded Unary Minus Operator (operator-()): You need to support negating your Matrix objects:
 
 Matrix a = {{1, 2}}; cout  
You should organize your project into the following files:
 
Matrix.h: This file should include the class prototype presented above as well as the prototypes for operator overloads that you implement. You MAY NOT modify the function prototypes that are included in the Matrix class prototype. However, you may add additional function prototypes and variables to the class prototype as needed. Make sure that this header file also includes a header guard (i.e., the #ifndef macro, etc.).
 
Matrix.cpp: This file should contain the implementation of your classs functions as well as the implementation of any operator overloads that you implement.
 
p1.cpp: This file should contain a small/moderately sized driver that demonstrates the full range of functionality of your Matrix class.
 
Additionally, make sure that you adhere to the following:
 
 All functions must be documented using Javadoc-style comments. Use inline documentation, as needed, to explain ambiguous or tricky parts of your code.
 
 
 
 
  typedef unsigned int uint; typedef initializer listkinitializer list> list class Matrix f public Matrix (uint rows, uint cols); constructor (all elements initialized to 0) Matrix const i list & list); constructor (using initializer list) Matrix (const Matrix & m) copy constructor destructor Matrix add scalar to this matrix Matrix add (double s) const; add this matrix and another matrix Matrix add const Matrix & m) const; Matrix subtract (double s) const; subtract scalar from this matrix subtract another matrix from this matrix Matrix subtract const Matrix & m) const; Matrix multiply (double s) const; multiply this matrix by a scaler Matrix multiply (const Matrix & m) const; multiply this matrix by another matrix divide this matrix by a scaler Matrix divide (double s) const; Matrix t const; transpose of this matrix const uint numRows C) const; returns the number of rows returns the number of cols const uint numCols const; double & at (uint row uint col) get/set element at row, col const double & at Guint row, uint col) const; get element at row, col (when using a const object) Matrix  typedef unsigned int uint; typedef initializer listkinitializer list> list class Matrix f public Matrix (uint rows, uint cols); constructor (all elements initialized to 0) Matrix const i list & list); constructor (using initializer list) Matrix (const Matrix & m) copy constructor destructor Matrix add scalar to this matrix Matrix add (double s) const; add this matrix and another matrix Matrix add const Matrix & m) const; Matrix subtract (double s) const; subtract scalar from this matrix subtract another matrix from this matrix Matrix subtract const Matrix & m) const; Matrix multiply (double s) const; multiply this matrix by a scaler Matrix multiply (const Matrix & m) const; multiply this matrix by another matrix divide this matrix by a scaler Matrix divide (double s) const; Matrix t const; transpose of this matrix const uint numRows C) const; returns the number of rows returns the number of cols const uint numCols const; double & at (uint row uint col) get/set element at row, col const double & at Guint row, uint col) const; get element at row, col (when using a const object) Matrix