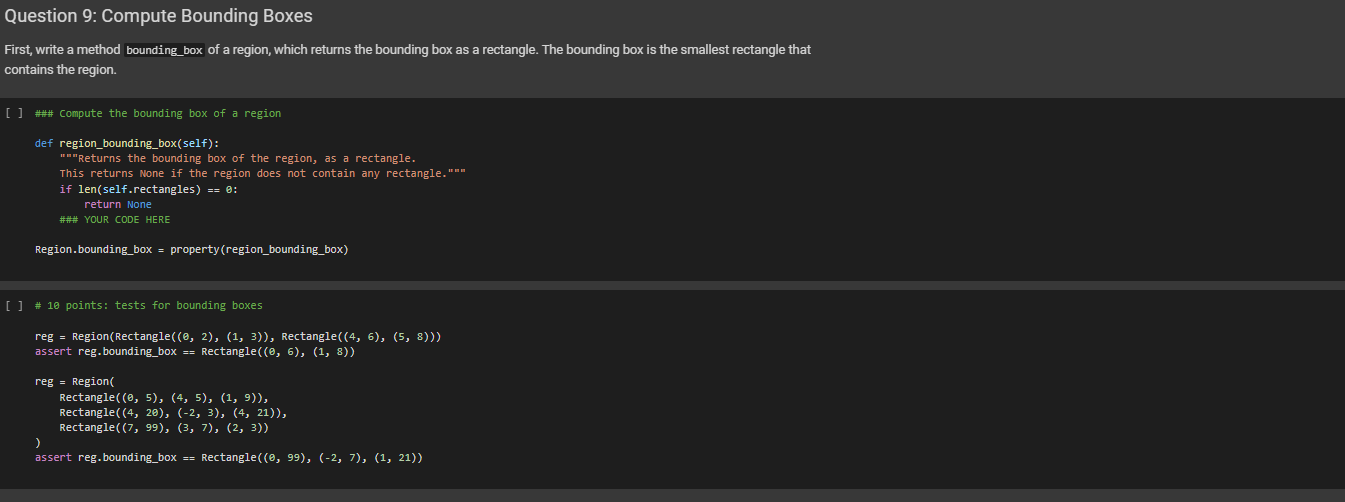
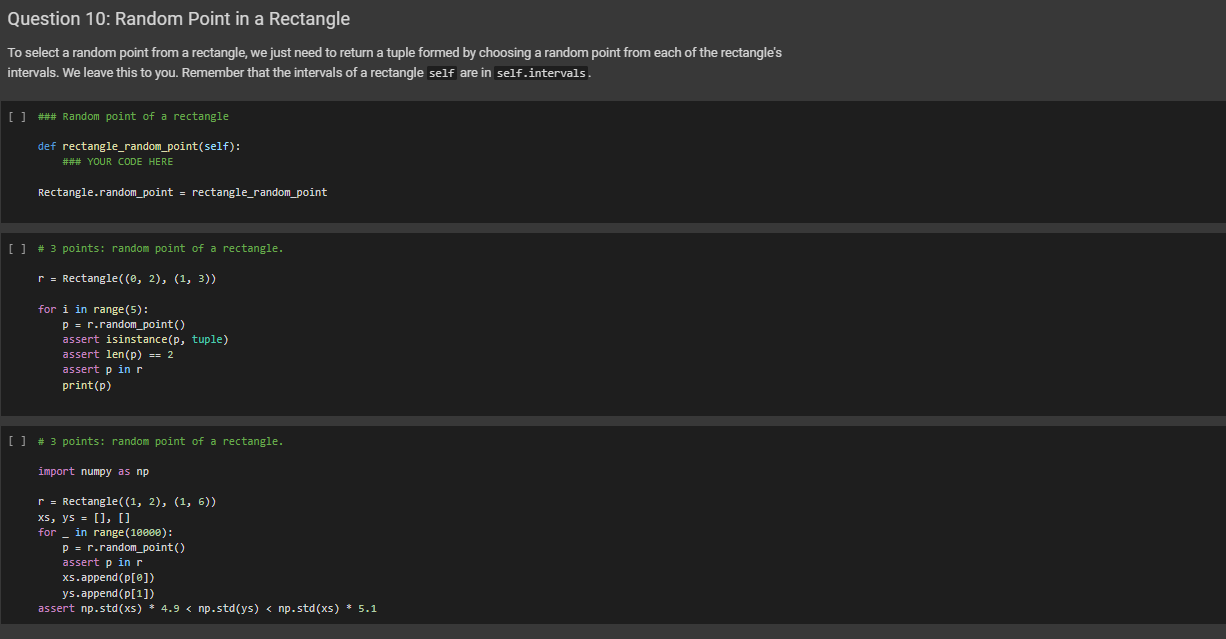
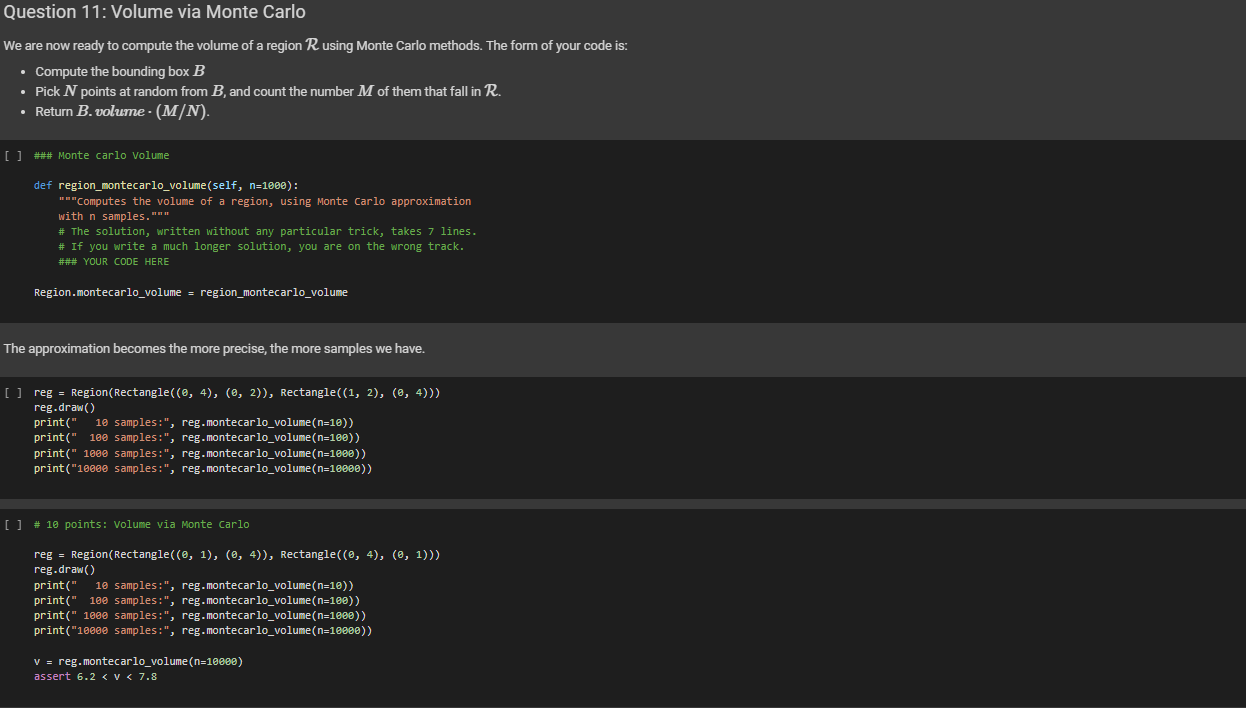
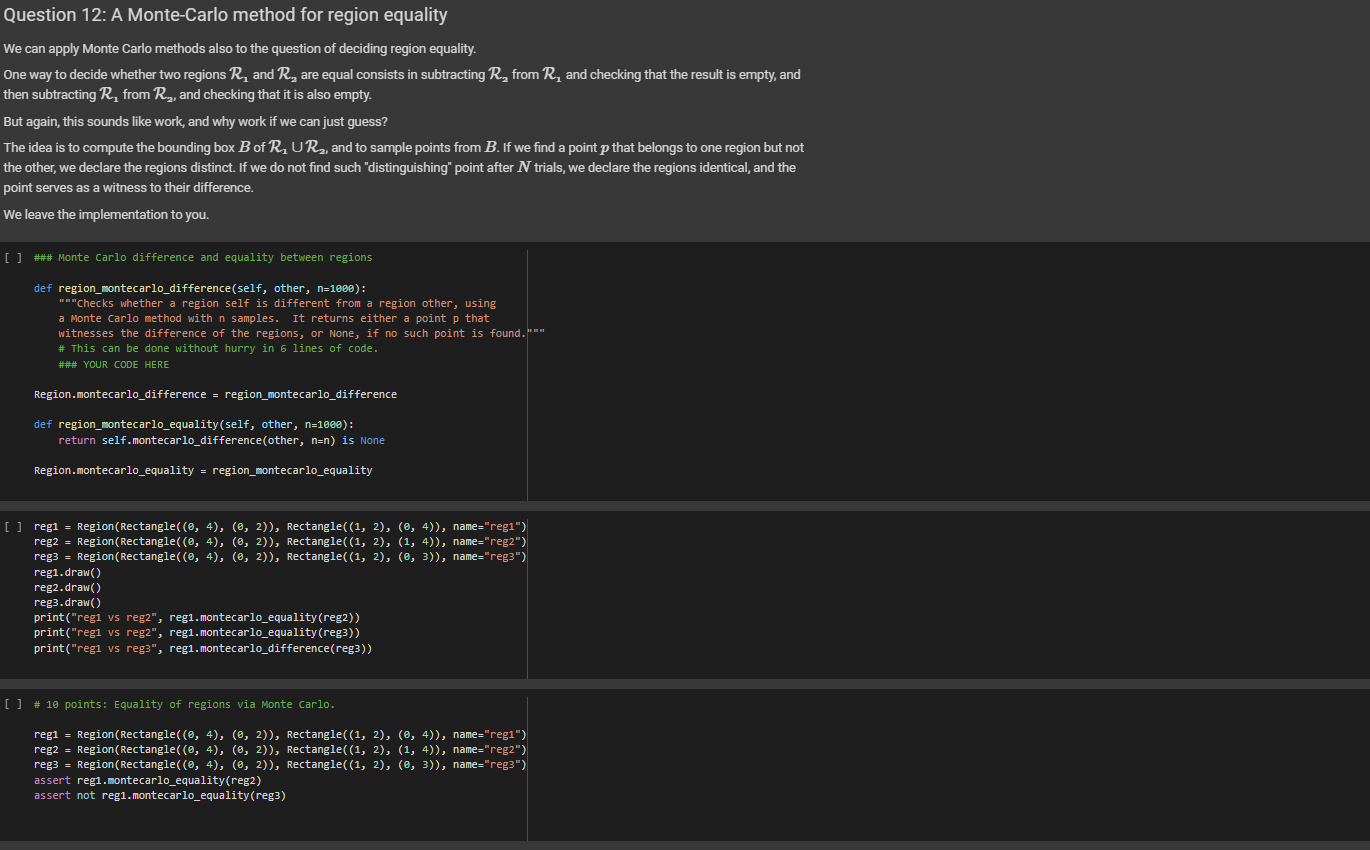
Rectangles Let us now develop a representation of a rectangle, in terms of intersection of intervals. We will phrase the definition in such a way that it works in any number of dimensions, storing the intervals as a list, as opposed to (say) storing the three intervals separately for 3D. import string class Rectangle(object): are or a no we def __init_(self, *intervals, name=None): ***A rectangle is initialized with a list, whose elements either Interval, a pair of numbers. It would be perhaps cleaner to accept only list of intervals, but specifying rectangles via a list of pairs, with each pair defining an interval, makes for a concise shorthand that will be useful in tests. Every rectangle has name, used to depict it. If name is provided, invent a random one. *** self. intervals = [] for i in intervals: self. intervals. append(i if type (i) Interval else Interval(*i)) # I want each rectangle to have is None: self.name = ". join random. choices (string, ascii_letters + string. digits, k=8)) else: self.name name name. if name = def __repr_(self): ***Function used to print a rectangle. *** = "Rectangle self.name + ": += repr([(i.x, i. xl) for i in self. intervals]) return + def clone (self, name=None): ***Returns a clone of itself, with a a given name. name name or self.name + return Rectangle(*self. intervals, name=name) = def _len_(self): ***Returns the number of dimensions of the rectangle def _len_(self): Returns the number of dimensions of the rectangle (not the length of the edges). This is used with _getitem__ below, to get the interval along dimension. return len(self. intervals) a def _getitem_(self, n): Returns the interval along the n-th dimension return self. intervals [n] def _setitem_(self, n, n, i): Sets the interval along the n-th dimension self. intervals[n] to be i** @property def ndims (self): ***Returns the number of dimensions of the interval. return len(self. intervals) @property def volume (self): return np. prod([i. length for i in self. intervals]) r [ ] print (Rectangle (Interval (3., 4.), Interval(1., 4.))) = Rectangle (Interval(1., 2.), (5., 6.), name=my_rectangle") print (r) print (r. clone()) Drawing rectangles Before we go much further, it is useful to be able to draw rectangles. Rectangles can have any number of dimensions, and we will write here code to draw them on 2D, projecting away all other dimensions. import matplotlib import matplotlib.pyplot as plt import matplotlib.path as mpath import matplotlib. patches as mpatches from matplotlib.collections import PatchCollection matplotlib.rcParams['figure.figsize'] = (6.0, 4.0) def draw_rectangles (*rectangles, prefix=""): ***Here, rectangles is a rectangle iterator; it could be a list, for instance. fig, = plt. subplots() patches = [] # We keep track of the limits. lo_x, hi_x = [], [] lo_y, hiy = [], [] for r in rectangles: x0, x1 = r[0]. endpoints() y0, y1 = r[1]. endpoints() lo_x. append(x0) hi_x. append(x1) lo_y. append(y) hi_y.append(y1) # Prepares the "patch" for the rectangle, see # https://matplotlib.org/api/_as_gen/matplotlib.patches. Rectangle.html = mpatches. Rectangle((x0, 0), x1 - x0, y1 - y0) y = (y + yl) / 2. - 0.0 x = (x + x1) / 2. - 0.0 plt. text(x, y, prefix + r. name, ha="center", family='sans-serif', size=12) patches. append (p) # Draws the patches. colors = np. linspace(0, 1, len(patches) + 1) collection = PatchCollection (patches, cmap=plt. cm. hsv, alpha=0.3) collection set_array(np. array(colors)) ax. add_collection(collection) # Computes nice ax limits. Note that I need to take care of the case # in which the rectangle lists are empty. = = r = see y lo_x, hi_x [], [] lo_y, hiy [], [] for in rectangles: xo, x1 = r[0]. endpoints() y0, y1 r[1]. endpoints) lo_x. append(x0) hi_x. append(x1) lo_y.append(yo) hi_y. append(yl) # Prepares the "patch" for the rectangle, # https://matplotlib.org/api/_as_gen/matplotlib. patches. Rectangle.html = mpatches. Rectangle((x0, 0), x1 - x0, y1 - y0) (y0 + yl) / 2. 0.0 (x + x1) / 2. 0.0 plt. text(x, y, prefix + r. name, ha="center", family='sans-serif', size=12) patches. append(p) # Draws the patches. colors np. linspace(0, 1, len(patches) + 1) collection = PatchCollection (patches, cmap=plt. cm. hsv, alpha=0.3) collection. set_array (np. array(colors)) ax. add_collection (collection) # Computes nice limits. Note that I need take of the # in which the rectangle lists empty. lux, hix (min(lo_x), max (hi_x)) if len(lo_x) > 0 else (0., 1.) loy, hiy = (min(lo_y), max (hi_y)) if len(loy) > 0 else (0., 1.) SX, sy hix lox, hiy loy lox 0.2 * hix += 0. 2 loy 0.2 hiy += 0.2 ax. set_xlim(lox, hix) ax. set_ylim (loy, hiy) plt. gca().set_aspect('equal', adjustable='box') plt. grid() plt. show() = ax to care case are = SX SX - sy [] r1 = Rectangle((3., 5.), (1., 4.), name="1") r2 Rectangle((1., 4.), (2., 6.), name="B") r3 Rectangle((2., 3.5), (1.5, 5.), name="C") draw_rectangles (r1, r2, r3) = There are three main operations on rectangles: intersection, union, and difference. Among them, only intersection is guaranteed to return another rectangle. In general, the union of two rectangles is ... two rectangles, and the difference between two rectangles is ... a whole lot of rectangles, as we will see. We let you implement rectangle equality, intersection, and membership of a point in a rectangle. Equality: Two rectangles R and Tare equal if they have the same number of dimensions, and if for every dimension k, the interval of R along k is equal to the interval of T along k. For example, Rectangle((2, 3), (4, 5)) == Rectangle((2, 3), (4, 5)) Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3)) Rectangle((2, 3), (4. 5)) != Rectangle((2, 3), (4, 5), (6, 7)) Intersection: The intersection is defined only if the rectangles have the same number of dimensions. The intersection is computed by taking the intersection of the intervals of the two rectangles for corresponding dimensions. Membership: For an n-dimensional point (20,21,...,xn) and an n-dimensional rectangle R, we have (20, 11, ..., In) e R if the point is in the region R. For instance: (2.5, 4.5) in Rectangle((2, 3), (4, 5)) (2, 3) in Rectangle ((2, 3), (4, 5)) (1, 3) not in Rectangle((2, 3), (4, 5)) If the point and the rectangle have different dimensions, you can raise a TypeError - Question 5: Rectangle Equality [] def rectangle_eq(self, other): ### YOUR CODE HERE Rectangle. _eq_ = rectangle_eq [] # 5 points: tests for rectangle equality. [] def rectangle_eq(self, other): ### YOUR CODE HERE Rectangle. eg = rectangle_eq [] # 5 points: tests for rectangle equality. assert Rectangle((2, 3), (4, 5)) Rectangle((2, 3), (4, 5)) assert Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3)) assert Rectangle((2, 3), (4, 5)) != Rectangle((2, 3), (4, 5), (6, 7)) Question 6: Rectangle Intersection ### Rectangle intersection and {} .format( def rectangle_and (self, other): if self.ndims != other. ndims: raise TypeError("The rectangles have different dimensions: {} self.ndims, other. ndims )) # Challenge: can you write this a one-liner shorter than this # There bonus points, note. Just for the fun. ### YOUR CODE HERE as Comment is? are no Rectangle. __and__ = rectangle_and [] # Let's how your rectangle intersection works. r1 Rectangle((2, 3), (0, 4)) r2 Rectangle(0, 4), (1, 3)) draw_rectangles (r1, r2) draw_rectangles (r1 & r2) = [] # 10 points: tests for rectangle intersection. = r1 r2 = Rectangle((2, 3), (0, 4)) Rectangle(0, 4), (1, 3)) r1 & r2 = Rectangle((2, 3), (1, 3)) assert Question 6: Rectangle Intersection [] ### Rectangle intersection def rectangle_and(self, other): if self.ndims != other.ndims: raise TypeError("The rectangles have different dimensions: {} and {}".format( self.ndims, other.ndims )) # Challenge: can you write this as a one-liner shorter than this comment is? # There are no bonus points, note. Just for the fun. ### YOUR CODE HERE Rectangle. __and__ = rectangle_and [ ] # Let's see how your rectangle intersection works. r1 = Rectangle((2, 3), (2, 4)) r2 = Rectangle((@, 4), (1, 3)) draw_rectangles(ri, r2) draw_rectangles (r1 & r2) [] # 10 points: tests for rectangle intersection. r1 = Rectangle((2, 3), (0, 4)) r2 = Rectangle((@, 4), (1, 3)) assert r1 & r2 == Rectangle((2, 3), (1, 3)) r1 = Rectangle((2, 3), (2, 4)) r2 = Rectangle((@, 4), (1, 5)) assert r1 & r2 == Rectangle((2, 3), (1, 4)) r1 = Rectangle((-1, 5), (@, 6)) r2 = Rectangle((@, 4), (-1, 3)) assert ri & r2 == Rectangle(0, 4), (0, 3)) r1 = Rectangle((2, 6), (0, 4)) r2 = Rectangle(0, 6), (2, 3)) assert ri & r2 == Rectangle((2, 6), (0, 3)) - Question 7: Point Membership in a Rectangle [] ### Membership of a point in a rectangle. def rectangle_contains(self, p): # The point is a tuple with one element per dimension of the rectangle. if len(p) != self.ndims: raise TypeError() ### YOUR CODE HERE Rectangle. _contains_ = rectangle_contains [] # 5 points: tests for membership. assert (2, 3) in Rectangle(0, 4), (1, 5)) assert (@, 4) in Rectangle((@, 4), (4, 5)) assert (4, 5) in Rectangle((@, 4), (4, 5)) assert (@, , 0) not in Rectangle((3, 4), (0, 3), (0, 8)) [] class Region (object): def __init__(self, *rectangles, name=None): "A region is initialized via a set of rectangles. *** self.rectangles = list(rectangles) if name is None: self.name = ".join( random.choices(string.ascii_letters + string.digits, k=8)) else: self.name = name def draw(self): draw_rectangles(*self.rectangles, prefix=self.name + ":") def _or_(self, other): "Union of regions."** return Region(*(self.rectangles + other.rectangles), name=self.name = "_union_" + other.name) [] # Let us try. r = Rectangle((@., 4.), (0., 4.), name="R") t = Rectangle((1.5, 3.5), (1., 5.), name="1") regi = Region(r, name="Regi") reg2 = Region(t, name="Reg2") (regi | reg2).draw() Question 8: Membership of a Point in a Region A point belongs into a region if it belongs into some rectangle of the region. We let you implement this. [] ### Membership of a point in a region def region_contains(self, p): ### YOUR CODE HERE Region. __contains__ - region_contains [] assert (2, 1) in Region (Rectangle((@, 2), (0, 3)), Rectangle((4, 6), (5, 8))) assert (2, 1) not in Region (Rectangle((@, 1), (, 3)), Rectangle((4, 6), (5, 8))) Question 9: Compute Bounding Boxes First, write a method bounding_box of a region, which returns the bounding box contains the region. a rectangle. The bounding box is the smallest rectangle that [ ] ### compute the bounding box of a region def region_bounding_box(self): "*"Returns the bounding box of the region, as a rectangle. This returns None if the region does not contain any rectangle." if len(self.rectangles) == 0: return None ### YOUR CODE HERE Region.bounding_box = property (region_bounding_box) [] # 10 points: tests for bounding boxes reg = Region (Rectangle((@, 2), (1, 3)), Rectangle((4, 6), (5, 8))) assert reg. bounding_box == Rectangle((@, 6), (1, 8)) reg = Region Rectangle((@, 5), (4, 5), (1, 9)), Rectangle((4, 20), (-2, 3), (4, 21)), Rectangle((7, 99), (3, 7), (2, 3)) ) assert reg. bounding_box == Rectangle((@, 99), (-2, 7), (1, 21)) Question 10: Random Point in a Rectangle To select a random point from a rectangle, we just need to return a tuple formed by choosing a random point from each of the rectangle's intervals. We leave this to you. Remember that the intervals of a rectangle self are in self.intervals [] ### Random point of a rectangle def rectangle_random_point(self): ### YOUR CODE HERE Rectangle.random_point = rectangle_random_point [] # 3 points: random point of a rectangle. r = Rectangle((@, 2), (1, 3)) for i in range(5): p = r.random_point() assert isinstance(P, tuple) assert len(P) == 2 assert p in r print(P) [] # 3 points: random point of a rectangle. import numpy as np r = Rectangle((1, 2), (1, 6)) xs, ys = [], [] for in range(10000): p = r.random_point() assert p in r xs.append(p[@]) ys.append(P[1]) assert np.std(xs) * 4.9 0 else (0., 1.) loy, hiy = (min(lo_y), max (hi_y)) if len(loy) > 0 else (0., 1.) SX, sy hix lox, hiy loy lox 0.2 * hix += 0. 2 loy 0.2 hiy += 0.2 ax. set_xlim(lox, hix) ax. set_ylim (loy, hiy) plt. gca().set_aspect('equal', adjustable='box') plt. grid() plt. show() = ax to care case are = SX SX - sy [] r1 = Rectangle((3., 5.), (1., 4.), name="1") r2 Rectangle((1., 4.), (2., 6.), name="B") r3 Rectangle((2., 3.5), (1.5, 5.), name="C") draw_rectangles (r1, r2, r3) = There are three main operations on rectangles: intersection, union, and difference. Among them, only intersection is guaranteed to return another rectangle. In general, the union of two rectangles is ... two rectangles, and the difference between two rectangles is ... a whole lot of rectangles, as we will see. We let you implement rectangle equality, intersection, and membership of a point in a rectangle. Equality: Two rectangles R and Tare equal if they have the same number of dimensions, and if for every dimension k, the interval of R along k is equal to the interval of T along k. For example, Rectangle((2, 3), (4, 5)) == Rectangle((2, 3), (4, 5)) Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3)) Rectangle((2, 3), (4. 5)) != Rectangle((2, 3), (4, 5), (6, 7)) Intersection: The intersection is defined only if the rectangles have the same number of dimensions. The intersection is computed by taking the intersection of the intervals of the two rectangles for corresponding dimensions. Membership: For an n-dimensional point (20,21,...,xn) and an n-dimensional rectangle R, we have (20, 11, ..., In) e R if the point is in the region R. For instance: (2.5, 4.5) in Rectangle((2, 3), (4, 5)) (2, 3) in Rectangle ((2, 3), (4, 5)) (1, 3) not in Rectangle((2, 3), (4, 5)) If the point and the rectangle have different dimensions, you can raise a TypeError - Question 5: Rectangle Equality [] def rectangle_eq(self, other): ### YOUR CODE HERE Rectangle. _eq_ = rectangle_eq [] # 5 points: tests for rectangle equality. [] def rectangle_eq(self, other): ### YOUR CODE HERE Rectangle. eg = rectangle_eq [] # 5 points: tests for rectangle equality. assert Rectangle((2, 3), (4, 5)) Rectangle((2, 3), (4, 5)) assert Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3)) assert Rectangle((2, 3), (4, 5)) != Rectangle((2, 3), (4, 5), (6, 7)) Question 6: Rectangle Intersection ### Rectangle intersection and {} .format( def rectangle_and (self, other): if self.ndims != other. ndims: raise TypeError("The rectangles have different dimensions: {} self.ndims, other. ndims )) # Challenge: can you write this a one-liner shorter than this # There bonus points, note. Just for the fun. ### YOUR CODE HERE as Comment is? are no Rectangle. __and__ = rectangle_and [] # Let's how your rectangle intersection works. r1 Rectangle((2, 3), (0, 4)) r2 Rectangle(0, 4), (1, 3)) draw_rectangles (r1, r2) draw_rectangles (r1 & r2) = [] # 10 points: tests for rectangle intersection. = r1 r2 = Rectangle((2, 3), (0, 4)) Rectangle(0, 4), (1, 3)) r1 & r2 = Rectangle((2, 3), (1, 3)) assert Question 6: Rectangle Intersection [] ### Rectangle intersection def rectangle_and(self, other): if self.ndims != other.ndims: raise TypeError("The rectangles have different dimensions: {} and {}".format( self.ndims, other.ndims )) # Challenge: can you write this as a one-liner shorter than this comment is? # There are no bonus points, note. Just for the fun. ### YOUR CODE HERE Rectangle. __and__ = rectangle_and [ ] # Let's see how your rectangle intersection works. r1 = Rectangle((2, 3), (2, 4)) r2 = Rectangle((@, 4), (1, 3)) draw_rectangles(ri, r2) draw_rectangles (r1 & r2) [] # 10 points: tests for rectangle intersection. r1 = Rectangle((2, 3), (0, 4)) r2 = Rectangle((@, 4), (1, 3)) assert r1 & r2 == Rectangle((2, 3), (1, 3)) r1 = Rectangle((2, 3), (2, 4)) r2 = Rectangle((@, 4), (1, 5)) assert r1 & r2 == Rectangle((2, 3), (1, 4)) r1 = Rectangle((-1, 5), (@, 6)) r2 = Rectangle((@, 4), (-1, 3)) assert ri & r2 == Rectangle(0, 4), (0, 3)) r1 = Rectangle((2, 6), (0, 4)) r2 = Rectangle(0, 6), (2, 3)) assert ri & r2 == Rectangle((2, 6), (0, 3)) - Question 7: Point Membership in a Rectangle [] ### Membership of a point in a rectangle. def rectangle_contains(self, p): # The point is a tuple with one element per dimension of the rectangle. if len(p) != self.ndims: raise TypeError() ### YOUR CODE HERE Rectangle. _contains_ = rectangle_contains [] # 5 points: tests for membership. assert (2, 3) in Rectangle(0, 4), (1, 5)) assert (@, 4) in Rectangle((@, 4), (4, 5)) assert (4, 5) in Rectangle((@, 4), (4, 5)) assert (@, , 0) not in Rectangle((3, 4), (0, 3), (0, 8)) [] class Region (object): def __init__(self, *rectangles, name=None): "A region is initialized via a set of rectangles. *** self.rectangles = list(rectangles) if name is None: self.name = ".join( random.choices(string.ascii_letters + string.digits, k=8)) else: self.name = name def draw(self): draw_rectangles(*self.rectangles, prefix=self.name + ":") def _or_(self, other): "Union of regions."** return Region(*(self.rectangles + other.rectangles), name=self.name = "_union_" + other.name) [] # Let us try. r = Rectangle((@., 4.), (0., 4.), name="R") t = Rectangle((1.5, 3.5), (1., 5.), name="1") regi = Region(r, name="Regi") reg2 = Region(t, name="Reg2") (regi | reg2).draw() Question 8: Membership of a Point in a Region A point belongs into a region if it belongs into some rectangle of the region. We let you implement this. [] ### Membership of a point in a region def region_contains(self, p): ### YOUR CODE HERE Region. __contains__ - region_contains [] assert (2, 1) in Region (Rectangle((@, 2), (0, 3)), Rectangle((4, 6), (5, 8))) assert (2, 1) not in Region (Rectangle((@, 1), (, 3)), Rectangle((4, 6), (5, 8))) Question 9: Compute Bounding Boxes First, write a method bounding_box of a region, which returns the bounding box contains the region. a rectangle. The bounding box is the smallest rectangle that [ ] ### compute the bounding box of a region def region_bounding_box(self): "*"Returns the bounding box of the region, as a rectangle. This returns None if the region does not contain any rectangle." if len(self.rectangles) == 0: return None ### YOUR CODE HERE Region.bounding_box = property (region_bounding_box) [] # 10 points: tests for bounding boxes reg = Region (Rectangle((@, 2), (1, 3)), Rectangle((4, 6), (5, 8))) assert reg. bounding_box == Rectangle((@, 6), (1, 8)) reg = Region Rectangle((@, 5), (4, 5), (1, 9)), Rectangle((4, 20), (-2, 3), (4, 21)), Rectangle((7, 99), (3, 7), (2, 3)) ) assert reg. bounding_box == Rectangle((@, 99), (-2, 7), (1, 21)) Question 10: Random Point in a Rectangle To select a random point from a rectangle, we just need to return a tuple formed by choosing a random point from each of the rectangle's intervals. We leave this to you. Remember that the intervals of a rectangle self are in self.intervals [] ### Random point of a rectangle def rectangle_random_point(self): ### YOUR CODE HERE Rectangle.random_point = rectangle_random_point [] # 3 points: random point of a rectangle. r = Rectangle((@, 2), (1, 3)) for i in range(5): p = r.random_point() assert isinstance(P, tuple) assert len(P) == 2 assert p in r print(P) [] # 3 points: random point of a rectangle. import numpy as np r = Rectangle((1, 2), (1, 6)) xs, ys = [], [] for in range(10000): p = r.random_point() assert p in r xs.append(p[@]) ys.append(P[1]) assert np.std(xs) * 4.9