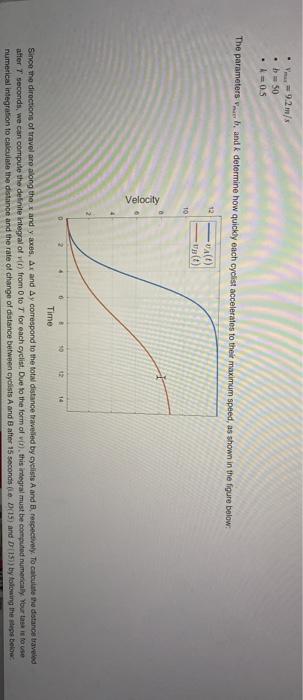
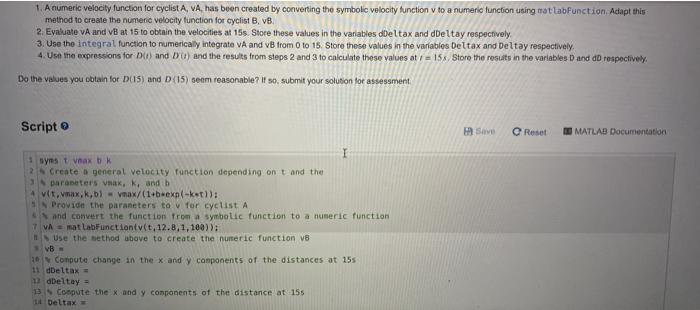
Related Rates Revisited: Obtaining the Distance Between Moving Objects My Solutio A common problem involves finding the rate, DX, at which the distance between two objects, Dois changing with time. An expression for D) can be found by noting that D() is determined by the difference in their 1 and y position components - Aud) and Ay(1) - and the relationship D = AXO:+Ayn? Differentiating this expression implicitly by and solving for D (0) yields the formular DA= ) () + y(1) (0) DO in practice, however, a formula for the x and y positions of the objects may not be known explicitly. For example we may only know their velocities x and y and their location at some initial time. This results in difficulty applying the formula above in cases where the velocities are non-constant. In these problems, however, integration can be used to compute the positions from the velocity functions Consider the problem or finding the distance between two cyclists that leave from the sale point at with cyclist Aheading Entut and cyclist heading North. Assume the velocities of the cyclists are approximated by the function Where for cyclist .-12.8m .b 100 and for cyclist b50 UBTYPIC 9.2./ b = 50 05 The parameters Verbandk determine how quickly each cyclist accelerates to their maximum speed, as shown in the figure below: 12 VA() valt) TO Velocity 0 0 50 12 14 Time Since the directions of travel are along the x and yaxes, Ax and Ay correspond to the total distance travelled by cyclists A and respectively. To calculate the distance traveled affer 7 seconds, we can compute the definite integral of vir) from 0 to 7 for each cyclist. Due to the form of vi). this integral must be computed numericaly. Your task is to use numerical integration to calculate the distance and the rate of change of distance between cylists A and B after 15 seconds. (15) and D (157) by flowing the steps below 1. A numeric velocity function for cyclist A, VA has been created by converting the symbolic velocity function v to a numeric function using matlabfunction Adapt this method to create the numere velocity function for cyclist B, VB. 2. Evaluate VA and B at 15 to obtain the velocities at 15s. Store these values in the variables Deltax and deltay respectively 3. Use the integral function to numerically integrate VA and VB from 0 to 15 Store these values in the variables Deltax and Deltay respectively. 4. Use the expressions for D) and D) and the results from steps 2 and 3 to calculate these values at y = 15% Store the results in the variables and respectively Do the values you obtain for D(15) and D (15) seem reasonable? If so, submit your solution for assessment Script Save Reset MATLAB Documentation I 1 syns tax bk Create a general velocity function depending on t and the parapeter's max, k, and b vit.,,b) - vnax/(1+b-exn-keti): Provide the parameters to v for cyclist A and convert the function from a symbolic function to a numeric function T VA = matlabFunctionivit, 12.8, 1.100)); Use the ethod above to create the numeric function V8 VB- Compute change in the x and y components of the distances at 155 11 deltax = 1 deltay B Compute the X and y components of the distance at 15 Deltax- Related Rates Revisited: Obtaining the Distance Between Moving Objects My Solutio A common problem involves finding the rate, DX, at which the distance between two objects, Dois changing with time. An expression for D) can be found by noting that D() is determined by the difference in their 1 and y position components - Aud) and Ay(1) - and the relationship D = AXO:+Ayn? Differentiating this expression implicitly by and solving for D (0) yields the formular DA= ) () + y(1) (0) DO in practice, however, a formula for the x and y positions of the objects may not be known explicitly. For example we may only know their velocities x and y and their location at some initial time. This results in difficulty applying the formula above in cases where the velocities are non-constant. In these problems, however, integration can be used to compute the positions from the velocity functions Consider the problem or finding the distance between two cyclists that leave from the sale point at with cyclist Aheading Entut and cyclist heading North. Assume the velocities of the cyclists are approximated by the function Where for cyclist .-12.8m .b 100 and for cyclist b50 UBTYPIC 9.2./ b = 50 05 The parameters Verbandk determine how quickly each cyclist accelerates to their maximum speed, as shown in the figure below: 12 VA() valt) TO Velocity 0 0 50 12 14 Time Since the directions of travel are along the x and yaxes, Ax and Ay correspond to the total distance travelled by cyclists A and respectively. To calculate the distance traveled affer 7 seconds, we can compute the definite integral of vir) from 0 to 7 for each cyclist. Due to the form of vi). this integral must be computed numericaly. Your task is to use numerical integration to calculate the distance and the rate of change of distance between cylists A and B after 15 seconds. (15) and D (157) by flowing the steps below 1. A numeric velocity function for cyclist A, VA has been created by converting the symbolic velocity function v to a numeric function using matlabfunction Adapt this method to create the numere velocity function for cyclist B, VB. 2. Evaluate VA and B at 15 to obtain the velocities at 15s. Store these values in the variables Deltax and deltay respectively 3. Use the integral function to numerically integrate VA and VB from 0 to 15 Store these values in the variables Deltax and Deltay respectively. 4. Use the expressions for D) and D) and the results from steps 2 and 3 to calculate these values at y = 15% Store the results in the variables and respectively Do the values you obtain for D(15) and D (15) seem reasonable? If so, submit your solution for assessment Script Save Reset MATLAB Documentation I 1 syns tax bk Create a general velocity function depending on t and the parapeter's max, k, and b vit.,,b) - vnax/(1+b-exn-keti): Provide the parameters to v for cyclist A and convert the function from a symbolic function to a numeric function T VA = matlabFunctionivit, 12.8, 1.100)); Use the ethod above to create the numeric function V8 VB- Compute change in the x and y components of the distances at 155 11 deltax = 1 deltay B Compute the X and y components of the distance at 15 Deltax