Question
Relational operators. Given two relations R(AB) with an instance containing 2 tuples, and S(BCD) with an instance containing 3 tuples. (a) Determine the minimum and
Relational operators. Given two relations R(AB) with an instance containing 2 tuples, and S(BCD) with an instance containing 3 tuples.
(a) Determine the minimum and maximum possible sizes (in terms of numbers of tuples and columns) for the result relation produced by each of the following relational algebra expressions. In each case, state any requirements or assumptions about the schemas for R and S that are needed to make the expression meaningful.
| RA expression | Requirements/ Assumptions | Min no. of tuples | Max no. of tuples | Max no. of columns | Min no. of columns |
| r |
|
|
|
|
|
|
|
|
|
|
|
|
|
| (Assuming A is an attribute in the schema of R)
|
|
|
|
|
(b) Reconsider the above problem, now with operator of natural join. Given two relations R(AB) with an instance containing 2 tuples, and S(BCD) with an instance containing 3 tuples. B is the only join attribute.
(i)Suppose there is no candidate key information available (i.e., for both relations, we dont know what the candidate keys are). What is the maximum number of tuples in the result of r |x| s? Under which condition will this happen? Provide a sample instance to illustrate the scenario. (Assuming domains of all attributes are integers.)
(ii)Now suppose the only candidate key for R is A and the only candidate key for S is B. Assuming that r(AB) still has 2 tuples, and s(BCD) still has 3 tuples. What is the maximum number of tuples in the joined result of r |x| s? Justify your answer.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


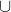 s
s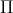 B (r)
B (r) 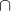
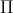 B (s)
B (s)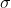 A=5 (r)
A=5 (r)