Repeat Example 1.2. Compute the velocity to t = 12 s, with a step size of 1 . Can you make any statement regarding the errors of the calculation based on the results?

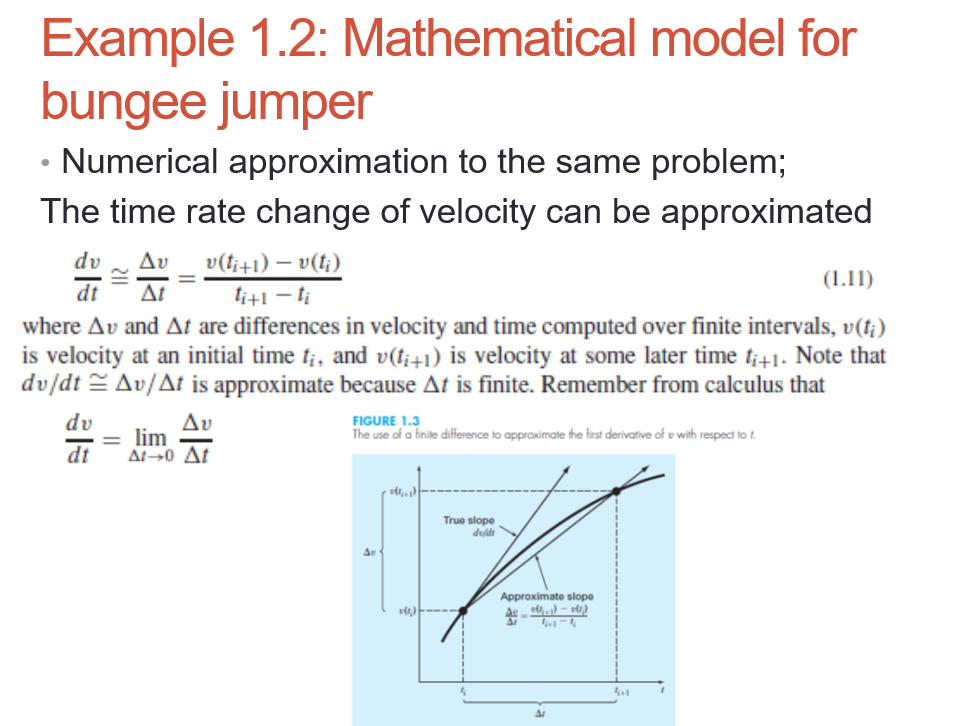
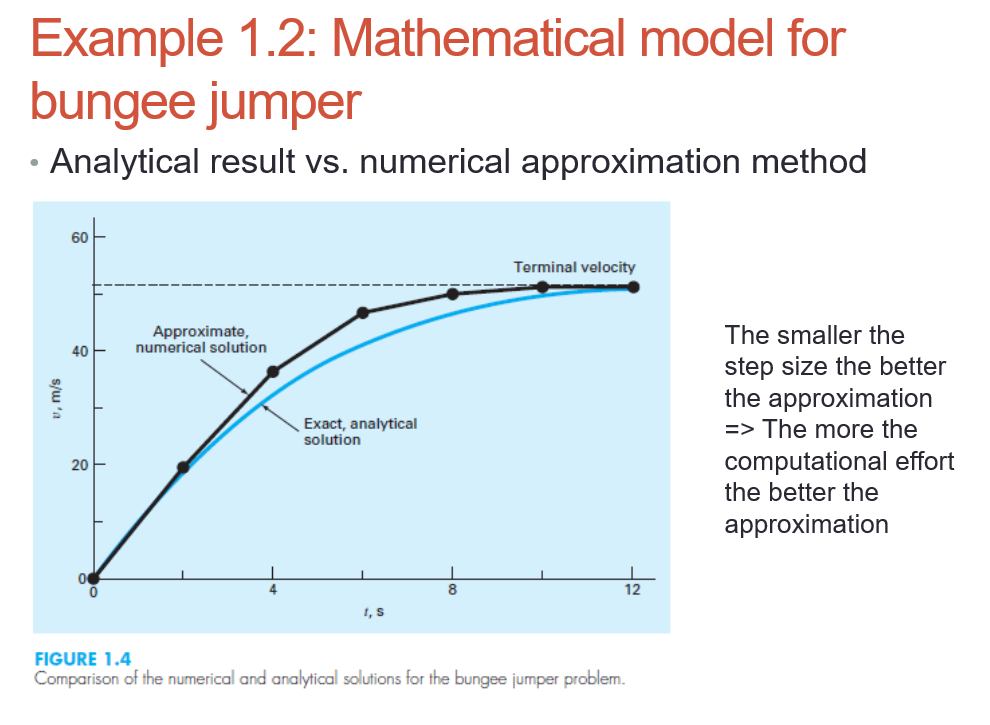
. Example 1.2: Mathematical model for bungee jumper Numerical approximation to the same problem; The time rate change of velocity can be approximated du Av v(t+1) - vti) dt (1.11) ti+l - t where Av and At are differences in velocity and time computed over finite intervals, v(ti) is velocity at an initial time t, and v(ti+1) is velocity at some later time ti+1. Note that dv/dt Av/At is approximate because At is finite. Remember from calculus that dv = lim The use of a finite difference to approximate the first derivative of v with respect to 1. dt A1-0 At FIGURE 1.3 True slope dude Av Approximate slope Ar.) - 1.1 Example 1.2: Mathematical model for bungee jumper Equation (1.11) is called a finite-difference approximation of the derivative at time ti. It can be substituted into Eq. (1.8) to give Cd v(ti+1) vti) ti+1 - ti = 8 du (t) = m This equation can then be rearranged to yield Numerical approximation v(ti+1) = v(ti) + (47]4+1 (1.12) m Notice that the term in brackets is the right-hand side of the differential equation itself [Eq. (1.8)]. That is, it provides a means to compute the rate of change or slope of v. Thus, the equation can be rewritten more concisely as du; Vi+I = V; + - dt (1.13) New value= old value + slope x step size (Euler's approximation) Example 1.2: Mathematical model for bungee jumper Solution. At the start of the computation (to = 0), the velocity of the jumper is zero. Using this information and the parameter values from Example 1.1, Eq. (1.12) can be used to compute velocity at t = 2 s: v=0+ 9.81 + [9.51 3103] 0.25 02|2 = 19.62 m/s 68.1 For the next interval (from t = 2 to 4 s), the computation is repeated, with the result v=19.62 + 19.81 +(9.81 035 (19.623] 0.25 68.1 (19.62)2 x 2 = 36.4137 m/s t, s v, m/s ONO.928 0 19.6200 36.4137 46.2983 50.1802 51.3123 51.6008 51.6938 10 12 Example 1.2: Mathematical model for bungee jumper Analytical result vs. numerical approximation method . 60 Terminal velocity Approximate, numerical solution 40 w, m/s Exact, analytical solution The smaller the step size the better the approximation => The more the comp nal effort the better the approximation 20 8 12 1,5 FIGURE 1.4 Comparison of the numerical and analytical solutions for the bungee jumper