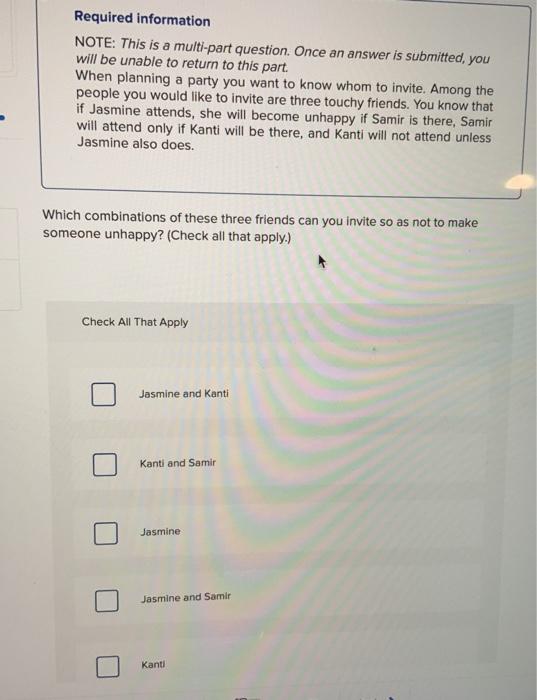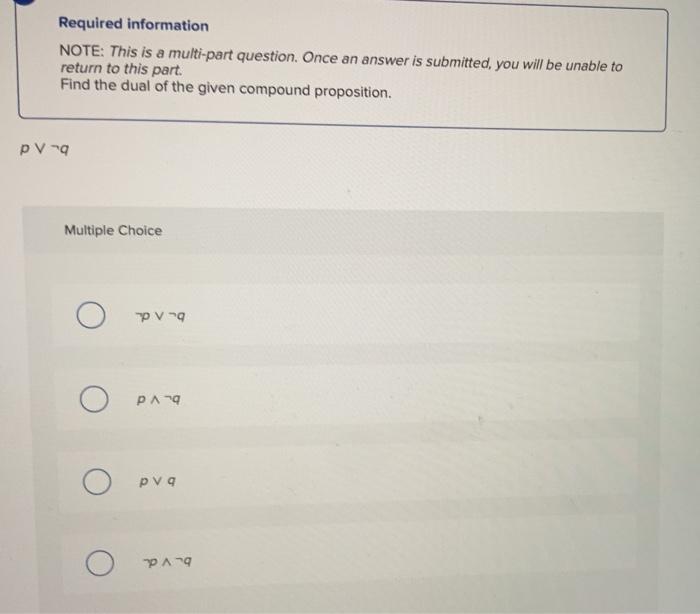
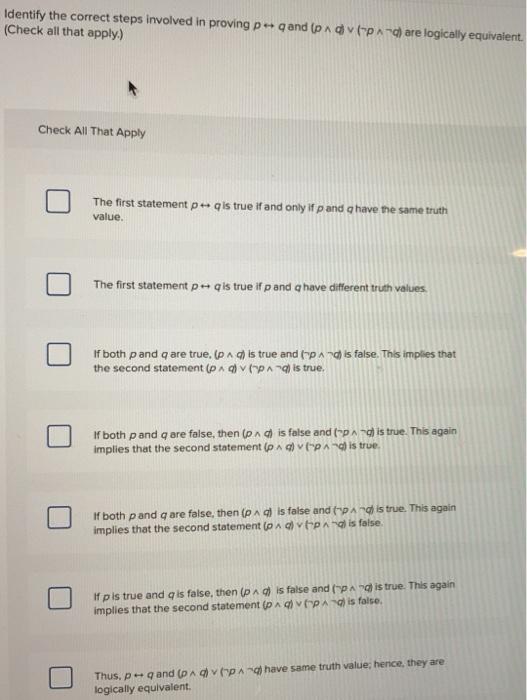

Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. When planning a party you want to know whom to invite. Among the people you would like to invite are three touchy friends. You know that if Jasmine attends, she will become unhappy if Samir is there, Samir will attend only if Kanti will be there, and Kanti will not attend unless Jasmine also does Which combinations of these three friends can you invite so as not to make someone unhappy? (Check all that apply.) Check All That Apply Jasmine and Kanti Kanti and Samir Jasmine Jasmine and Samir Kanti Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part Prove the given expression is a tautology by developing a series of logical equivalence to demonstrate that it is logically equivalent to T. 160-119 - 11 - 6-1 1 [Cp - )^(-1) -(0-1 2 - - - ] (p-= (4-2) (QAY( by logical equivalence 3 T by domination law 4160-4) (q + 7) + (0-9 = 160+) (Oy - by logical equivalence 3 (qv) (pvn) by associative law low 6 Tv (pvn) by negation law 7 -----] (0 ) by De Morgan's low 4 IGOV p) A (max]] [[rva) ArvM] by distributive law 1 [-(-av-] (0-1)=(pva Il gyorsfagyl by logical equivalence (o TavP)] v Irva) 4F] by negation CI ITA(V)virg) AT] by negation 12 (-v-p) virva) by identity law (3 (0A - Q4 27 V60 - ) = (^ )v (a Adv(pv) by logical equivalence It (provv(QA)va) (volanavn by logical equivalence B (DA) (QA) by commutative law 16 (pa-purv (94-) by Ocelotive-low low Reset Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Find the dual of the given compound proposition. PV-a Multiple Choice V o para o ova PA-9 Identify the correct steps involved in proving pand (pAdv(pdare logically equivalent. (Check all that apply.) Check All That Apply The first statement p q is true if and only if pand have the same truth value. The first statement pls true if p and have different truth values that If both pand q are true. God is true and pand is false. This implies th the second statement (pAdvpng) is true. If both pand q are false, then lod) is false and ("pand is true. This again implies that the second statement ( pa) (pach is true. If both pand care false, then (pad is false and trand is true. This again implies that the second statement ( odvtpad is false If pis true and is false, then (pa) is false and langis true. This again implies that the second statement (papan) is false. Thus, pq and (Advand have same truth value; hence, they are logically equivalent Click and drag the statements to show that p) and pq are logically equivalent. The proposition (p+q) is true when p and q do not have the same truth values fit pis true, then qis false, and vice versa). These are exactly the cases in which p- - is true. Therefore these two expressions are true in exactly the same instances, and therefore are logically equivalent. The proposition (p) is true when p and q have the same truth values. tp and q are either true or false.) These are exactly the case in which pq is true. Reset