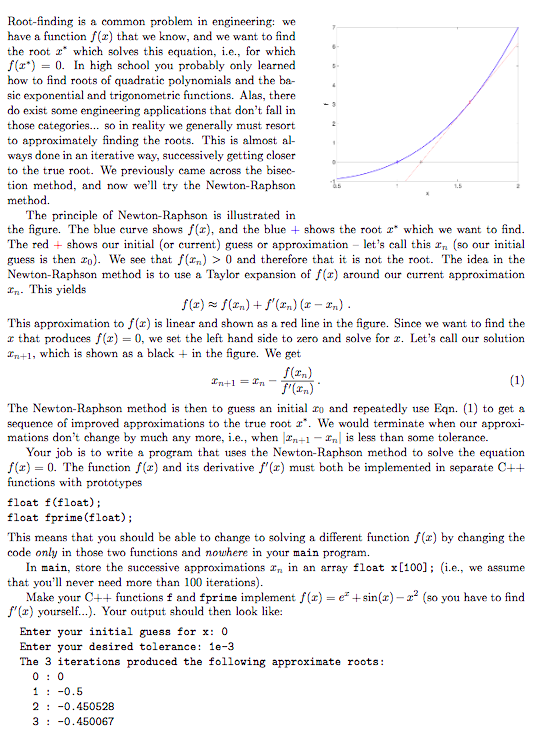
Root-finding is a common problem in engineering: we have a function f(z) that we know, and we want to find the root which solves ths equation, i.e., for which f(x*) 0, In high school you probably only learned how to find roots of quadratic polynomials and the ba- sic exponential and trigonometric functions. Alas, there do exist some engineering applications that don't fall in those categories... so in reality we generally must resort to approximately finding the roots. This is almost al- ways done in an iterative way, successively getting closer to the true root. We previously came across the bisec- tion method, and now we'll try the Newton-Raphson method. s The principle of Newton-Raphson is lustrated in the figure. The blue curve shows f (), and the blueshows the root which we want to find The red shows our initial (or current) guess or approximation let's call this so our initial guess is then zo). We see that f(rn) > 0 and therefore that it is not the root. The idea in the Newton-Raphson method is to use a Taylor expansion of f(a) around our current approximation rn. This yields This approximation to f(r) is linear and shown as a red line in the figure. Since we want to find the r that produces f(z) = 0, we set the left hand side to zero and solve for z. Let's call our solution r+1, which is shown as a black in the figure. We get The Newton-Raphson method is then to guess an initial ro and repeatedly use Eqn. (1) to get a sequence of improved approximations to the true root x". We would terminate when our approx mations don't change by much any more, i.e., when is less than some tolerance. Your job is to write a program that uses the Newton-Raphson method to solve the equation f(x)-0. The function f(z) and its derivative f'(x) must both be implemented in separate C++ functions with prototypes float f(float) float fprime (float); This means that you should be able to change to solving a different function f(z) by changing the code only in those two functions and nowhere in your main program. In main, store the successive approximations r in an array float x[100]; (i.e., we assume that you'll never need more than 100 iterations) Make your Cfunctions f and fprime implement f(z) = ez +sin(x)-z? (so you have to find f(r yourself). Your output should then look like: Enter your initial guess for x: 0 Enter your desired tolerance: 1e-3 The 3 iterations produced the following approximate roots: 1-0.5 2-0.450528 3:-0.450067