Question
Satellite applications motivated the development of a silver-zinc battery. Table (1) contains failure data collected to characterize the performance of the battery during its life
Satellite applications motivated the development of a silver-zinc battery. Table (1) contains failure data collected to characterize the performance of the battery during its life cycle. Use these data.
Table (1) (table.csv)
Special note: Please solve it using R. Also try to elaborate without skipping steps.
Link to download the full questions: https://drive.google.com/file/d/1Qvnp9Q0axA8jKW9Yk4MnK5xEU11q2CRM/view?usp=sharing
| X1 | X 2 | X 3 | X 4 | X 5 | y |
| 0.375 | 3.13 | 60.0 | 40 | 2.00 | 101 |
| 1.000 | 3.13 | 76.8 | 30 | 1.99 | 141 |
| 1.000 | 3.13 | 60.0 | 20 | 2.00 | 96 |
| 1.000 | 3.13 | 60.0 | 20 | 1.98 | 125 |
| 1.625 | 3.13 | 43.2 | 10 | 2.01 | 43 |
| 1.625 | 3.13 | 60.0 | 20 | 2.00 | 16 |
| 1.625 | 3.13 | 60.0 | 20 | 2.02 | 188 |
| 0.375 | 5.00 | 76.8 | 10 | 2.01 | 10 |
| 1.000 | 5.00 | 43.2 | 10 | 1.99 | 3 |
| 1.000 | 5.00 | 43.2 | 30 | 2.01 | 386 |
| 1.000 | 5.00 | 100.0 | 2 | 2.00 | 45 |
| 1.625 | 5.00 | 76.8 | 10 | 1.99 | 2 |
| 0.375 | 1.25 | 76.8 | 10 | 2.01 | 76 |
| 1.000 | 1.25 | 43.2 | 10 | 1.99 | 78 |
| 1.000 | 1.25 | 76.8 | 30 | 2.00 | 160 |
| 1.000 | 1.25 | 60.0 | 0 | 2.00 | 3 |
| 1.625 | 1.25 | 43.2 | 30 | 1.99 | 216 |
| 1.625 | 1.25 | 60.0 | 20 | 2.00 | 73 |
| 0.375 | 3.13 | 76.8 | 30 | 1.99 | 314 |
| 0.375 | 3.13 | 60.0 | 20 | 2.00 | 170 |
X1 - Charge rate (amps) X2 - Discharge rate (amps) X3 - Depth of discharge (% of rated ampere-hours) X4 - Temparature (0C) X5 - End of Charge Voltage (Volts) Y - Cycles to failure


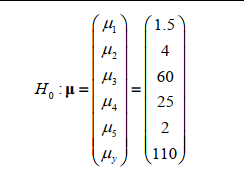
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


