Question
Search problem: The search problem is to take a sorted array A[1,...,n] and an element x and either find a location of x in A

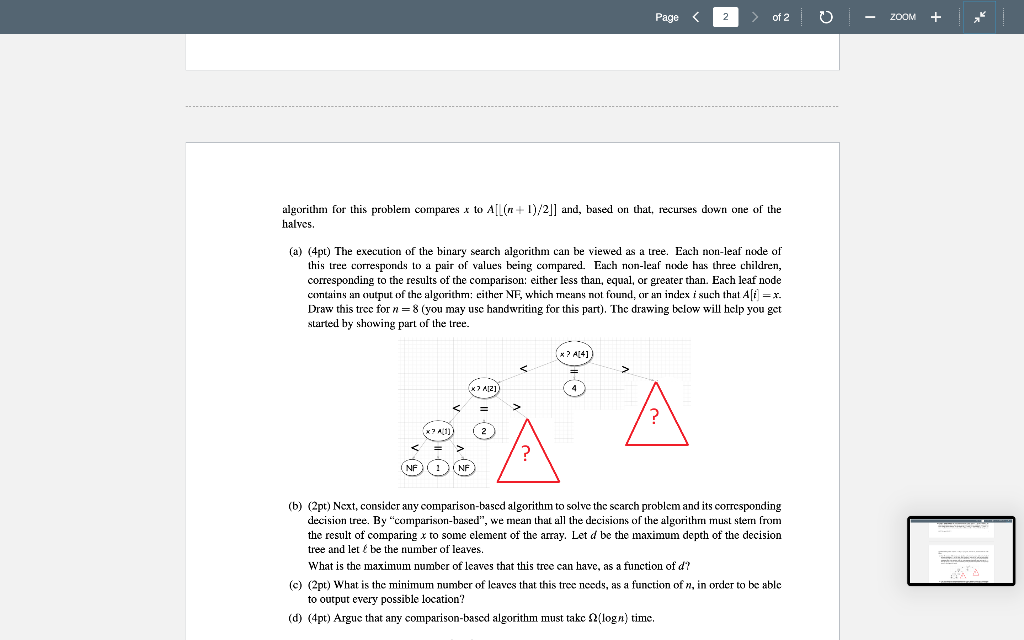 Search problem: The search problem is to take a sorted array A[1,...,n] and an element x and either find a location of x in A or report that one does not exist. Notice that we are indexing the array starting from 1. For the sake of simplicity, you may assume that n is a power of 2. For example, if A = (4,9,11,57) and x = 9, then the answer to the search problem is 2 because A[2] = 9. Recall that the binary search CMPSC 465, Spring 2023, HW 3 1 algorithm for this problem compares x to A[(n + 1)/2] and, based on that, recurses down one of the halves. (a) (4pt) The execution of the binary search algorithm can be viewed as a tree. Each non-leaf node of this tree corresponds to a pair of values being compared. Each non-leaf node has three children, corresponding to the results of the comparison: either less than, equal, or greater than. Each leaf node contains an output of the algorithm: either NF, which means not found, or an index i such that A[i] = x. Draw this tree for n = 8 (you may use handwriting for this part). The drawing below will help you get started by showing part of the tree. (b) (2pt) Next, consider any comparison-based algorithm to solve the search problem and its corresponding decision tree. By comparison-based, we mean that all the decisions of the algorithm must stem from the result of comparing x to some element of the array. Let d be the maximum depth of the decision tree and let be the number of leaves. What is the maximum number of leaves that this tree can have, as a function of d? (c) (2pt) What is the minimum number of leaves that this tree needs, as a function of n, in order to be able to output every possible location? (d) (4pt) Argue that any comparison-based algorithm must take (log n) time.
Search problem: The search problem is to take a sorted array A[1,...,n] and an element x and either find a location of x in A or report that one does not exist. Notice that we are indexing the array starting from 1. For the sake of simplicity, you may assume that n is a power of 2. For example, if A = (4,9,11,57) and x = 9, then the answer to the search problem is 2 because A[2] = 9. Recall that the binary search CMPSC 465, Spring 2023, HW 3 1 algorithm for this problem compares x to A[(n + 1)/2] and, based on that, recurses down one of the halves. (a) (4pt) The execution of the binary search algorithm can be viewed as a tree. Each non-leaf node of this tree corresponds to a pair of values being compared. Each non-leaf node has three children, corresponding to the results of the comparison: either less than, equal, or greater than. Each leaf node contains an output of the algorithm: either NF, which means not found, or an index i such that A[i] = x. Draw this tree for n = 8 (you may use handwriting for this part). The drawing below will help you get started by showing part of the tree. (b) (2pt) Next, consider any comparison-based algorithm to solve the search problem and its corresponding decision tree. By comparison-based, we mean that all the decisions of the algorithm must stem from the result of comparing x to some element of the array. Let d be the maximum depth of the decision tree and let be the number of leaves. What is the maximum number of leaves that this tree can have, as a function of d? (c) (2pt) What is the minimum number of leaves that this tree needs, as a function of n, in order to be able to output every possible location? (d) (4pt) Argue that any comparison-based algorithm must take (log n) time.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


