Secant Method in Python 3 for a 1D Problem
 Secant Method
Secant Method
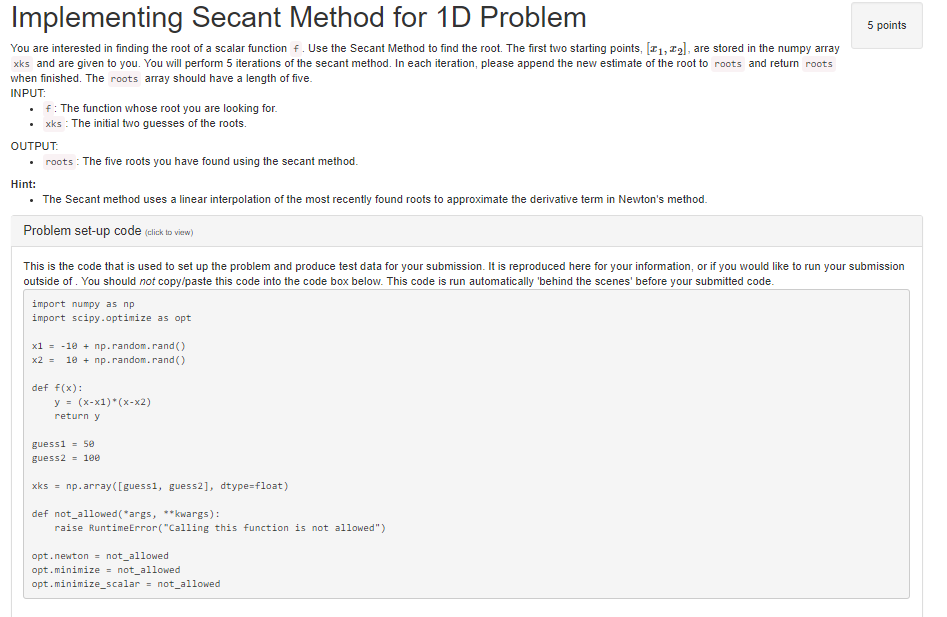
Implementing Secant Method for 1D Problem 5 points You are interested in finding the root of a scalar function f. Use the Secant Method to find the root. The first two starting points, [z1,z2, are stored in the numpy array xks and are given to you. You will perform 5 iterations of the secant method. In each iteration, please append the new estimate of the root to roots and return roots when finished. The roots array should have a length of five INPUT .F: The function whose root you are looking for. . xks The initial two guesses of the roots OUTPUT .roots The five roots you have found using the secant method Hint: . The Secant method uses a linear interpolation of the most recently found roots to approximate the derivative term in Newton's method Problem set-up code (click to view) This is the code that is used to set up the problem and produce test data for your submission. It is reproduced here for your information, or if you would like to run your submission outside of. You should not copy/paste this code into the code box below. This code is run automatically 'behind the scenes' before your submitted code import numpy as np import scipy.optimize as opt x1-1np.random.rand() x21np.random.rand() def f(x): y? (x-x1 ) * (x-x2) return y guessi 5 guess2 18e xksnp.array(Iguessl, guess2], dtype-float) def not_allowed( args, **kwargs): raise RuntimeError( "Calling this function is not allowed") opt.newton not_allowed opt.minimize not_allowed opt . minimize-scalar not-allowed Implementing Secant Method for 1D Problem 5 points You are interested in finding the root of a scalar function f. Use the Secant Method to find the root. The first two starting points, [z1,z2, are stored in the numpy array xks and are given to you. You will perform 5 iterations of the secant method. In each iteration, please append the new estimate of the root to roots and return roots when finished. The roots array should have a length of five INPUT .F: The function whose root you are looking for. . xks The initial two guesses of the roots OUTPUT .roots The five roots you have found using the secant method Hint: . The Secant method uses a linear interpolation of the most recently found roots to approximate the derivative term in Newton's method Problem set-up code (click to view) This is the code that is used to set up the problem and produce test data for your submission. It is reproduced here for your information, or if you would like to run your submission outside of. You should not copy/paste this code into the code box below. This code is run automatically 'behind the scenes' before your submitted code import numpy as np import scipy.optimize as opt x1-1np.random.rand() x21np.random.rand() def f(x): y? (x-x1 ) * (x-x2) return y guessi 5 guess2 18e xksnp.array(Iguessl, guess2], dtype-float) def not_allowed( args, **kwargs): raise RuntimeError( "Calling this function is not allowed") opt.newton not_allowed opt.minimize not_allowed opt . minimize-scalar not-allowed
 Secant Method
Secant Method





