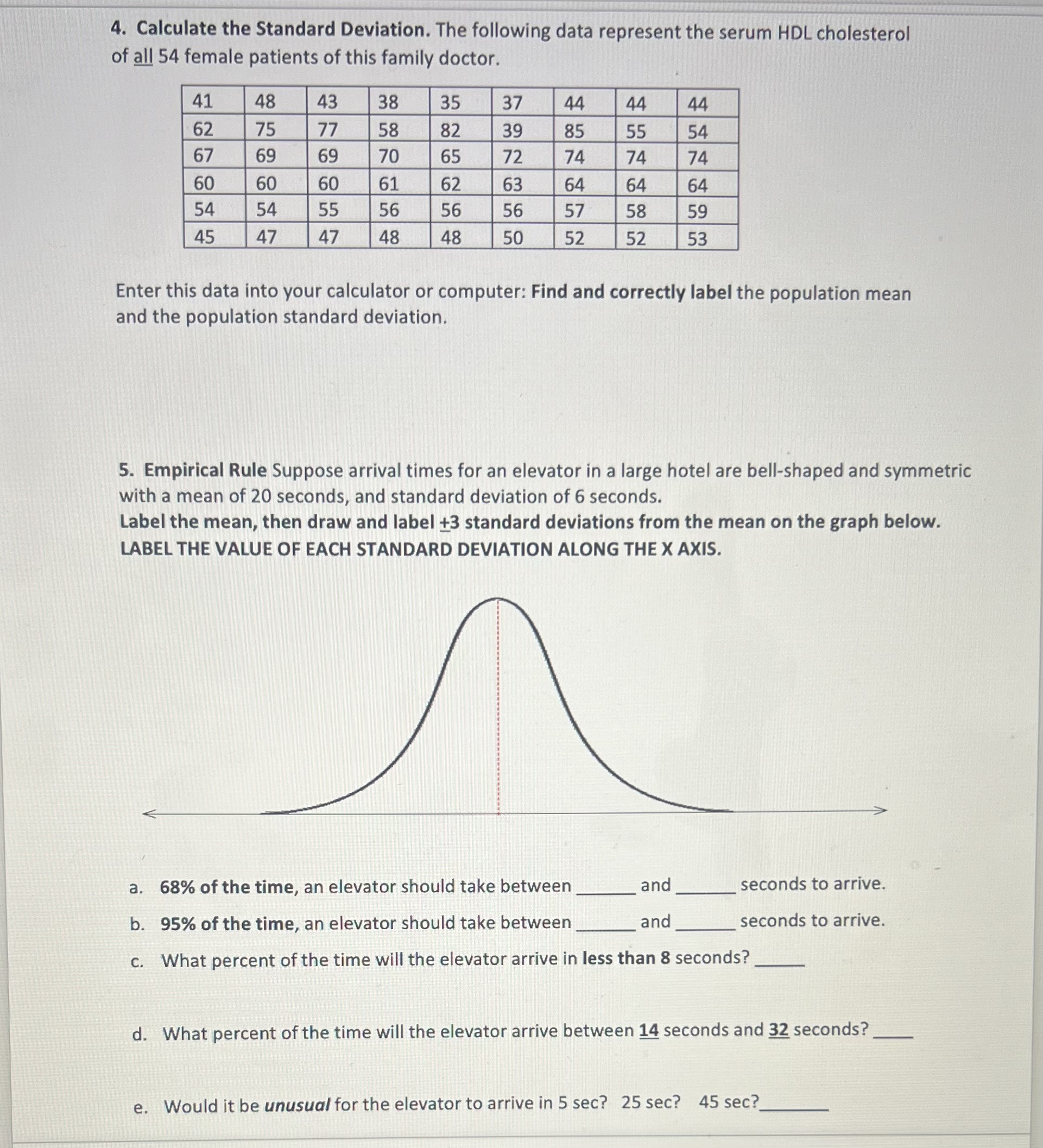
Section 3.2 Measure of the Spread 1. Answer the following questions: a. The the mean, on the average. is a measure of how far the values in a data set are from b. The variance is computed slightly differently for and c. When a data set has a bell-shaped histogram, it is often possible to use the standard deviation to provide an approximate description of the data using a rule known as 2. Symbol Summary Number of Data Values Mean Standard Deviation Variance Population Sample 3. Calculate the Standard Deviation. The following data represent the serum HDL cholesterol from a sample of 18 female patients of a family doctor. 41 48 43 38 35 37 44 44 44 62 75 77 58 82 39 85 55 54 Enter this data into your calculator: Find and correctly label the sample mean and the sample standard deviation. 4. Calculate the Standard Deviation. The following data represent the serum HDL cholesterol of all 54 female patients of this family doctor. 41 48 43 38 35 37 44 44 44 62 75 77 58 82 39 85 55 54 67 69 69 70 65 72 74 74 74 60 60 60 61 62 63 64 64 64 54 54 55 56 56 56 57 58 59 45 47 47 48 48 50 52 52 53 Enter this data into your calculator or computer: Find and correctly label the population mean and the population standard deviation. 5. Empirical Rule Suppose arrival times for an elevator in a large hotel are bell-shaped and symmetric with a mean of 20 seconds, and standard deviation of 6 seconds. Label the mean, then draw and label +3 standard deviations from the mean on the graph below. LABEL THE VALUE OF EACH STANDARD DEVIATION ALONG THE X AXIS. a. 68% of the time, an elevator should take between b. 95% of the time, an elevator should take between c. What percent of the time will the elevator arrive in less than 8 seconds? and and seconds to arrive. seconds to arrive. d. What percent of the time will the elevator arrive between 14 seconds and 32 seconds? e. Would it be unusual for the elevator to arrive in 5 sec? 25 sec? 45 sec? Section 3.3 Measures of Position 1. The z-score of an individual data value tells how many that value is from its population mean. 2. The denoted Q separates the lowest of the data from the highest 3. The denoted Q2 separates the lowest of the data from the highest 4. The of the data from the highest 5. divide a data set into hundredths. Q2 is the same as the median. denoted Q3 separates the lowest 6. In general, the kth Percentile(denoted Pk) of a data set is a value that means: k% of the data are 7. An this value. is a value that is considerably larger or considerably smaller than most of the values in a data set. 8. The interquartile range is found by subtracting the quartile from the quartile. 9. The of a data set consists of the median, the first quartile, the third quartile, the smallest value, and the largest value. These values are generally arranged in order. 10. A is a graph that presents the five-number summary along with some additional information about a data set. There are several different kinds of boxplots. The one we describe here is sometimes called a 2. Standard Scores (Z-Score). Which is better compared to your classmates: a. You got a 72 on a quiz where the class mean = 60, and stan.dev.= 5, interpret using the z-score. wwwwwwwwwww z-score= b. You got a 86 on a quiz where the class mean = 80, and stan dev = 4 z-score= c. What would it mean if you had a z-score of in a class mean = 60, stan dev=5? z = 1.2? z=2.8? z=-1.1? z=-32 z=0.2