SET A:

The quantity of clients hanging tight for blessing wrap administration at a retail chain is a rv X with potential qualities 0, 1, 2, 3, 4 and comparing probabilities 0.1, 0.2, 0.3, 0.25, 0.15. A haphazardly chosen client will have 1, 2, or 3 bundles for wrapping with probabilities 0.5, 0.25, and 0.25, separately. Let Y = the complete number of bundles to be wrapped for the clients holding up in line (accept that the quantity of bundles put together by one client is autonomous of the number presented by some other client).

(a)

Decide P(X = 3, Y = 3), i.e., p(3, 3). (Round your response to four decimal spots.)

P(X = 3, Y = 3) =

(b)

Decide p(4, 11). (Round your response to four decimal spots.)

p(4, 11) =

A teacher has given a short test comprising of two sections. For a haphazardly chosen understudy, let X = the quantity of focuses acquired on the initial segment and Y = the quantity of focuses procured on the subsequent part. Assume that the joint pmf of X and Y is given in the going with table.

y

p(x, y)

0 5 10 15

x 0 0.03 0.06 0.02 0.10

5 0.04 0.17 0.20 0.10

10 0.01 0.15 0.11 0.01

(a) Compute the covariance for X and Y. (Round your response to two decimal spots.)

Cov(X, Y) =

(b) Compute ? for X and Y. (Round your response to two decimal spots.)

i6i

? =

The normal number of Hate Crimes in the United States each year (1991 to 2018) is roughly 7900 every year with a standard deviation of around

1200 disdain wrongdoings each year.

In what reach would you hope to track down the center 95% of disdain violations each year?

Among Incorrect and Incorrect.

If you somehow happened to draw an example of 10 years' worth of disdain violations, in what reach would you hope to track down the center 95% of normal number of Hate Crimes each year in this example?

Between Incorrect a

Passable mechanical properties for foundational layout

of metallic aviation vehicles requires a supported

technique for genuinely examining exact test information.

The article "Setting up Mechanical Property

Allowables for Metals" (J. of Testing and Evaluation,

1998: 293-299) utilized the going with information on tractable

extreme strength (ksi) as a reason for tending to

the troubles in growing such a technique.

122.2 124.2 124.3 125.6 126.3 126.5 127.2 127.3

127.5 127.9 128.6 128.8 129.0 129.2 129.4 129.6 130.2

130.4 130.8 131.3 131.4 131.5 131.6 131.8

131.8 132.3 132.4 132.5 132.6

132.7 132.9 133.0 133.1 133.2

133.2 133.3 133.5 133.8 133.9 134.0

134.0 134.1 134.2 134.3 134.4 134.6

134.7 134.8 134.9 135.2

135.2 135.3 135.4 135.5 135.6

135.7 135.8 135.9

135.9 136.0 136.1 136.2 136.3 136.4

136.6 136.8 136.9 137.0 137.1 137.2 137.6

137.8 137.9 138.2 138.3

138.4 138.5 138.6 138.7 139.0

139.1 139.5 139.6 139.8 140.0 140.7

140.9 141.2 141.4 141.5 141.6 142.9 143.4 143.5

143.6 143.8 143.9 144.1 144.5 147.7

b. Develop a histogram utilizing equivalent width classes

with the five star having a lower breaking point of 122 and an

furthest constraint of 124. At that point remark on any fascinating

highlights of the histogram.

SET B:

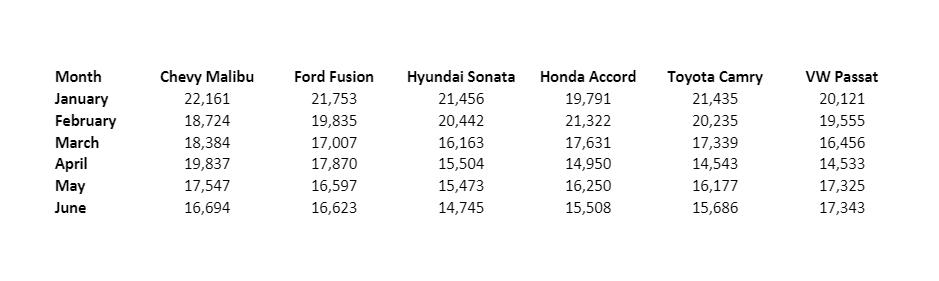
The spreadsheet entitled Compact Cars has sales data for six of the top automobile models, over a six-month period in 2019. There are no sales for the whole/complete of 2019-year sales data meaning what is available is a sample of the 2019-year sales. Your task is to test both: if the mean number of automobile types sold is significantly different for all of the six models AND whether or not the mean number of automobiles sold per month is significantly different among the months (Some of these tests will be taught in a later part of the class under "Hypothesis Testing" & ANOVA). The sample of automobile sales data for 2019 is in the Excel file provided. So, first do the following tests and conclude the findings (these have been taught in class):

Month Chevy Malibu Ford Fusion Hyundai Sonata Honda Accord Toyota Camry VW Passat January 22,161 21,753 21,456 19,791 21,435 20,121 February 18,724 19,835 20,442 21,322 20,235 19,555 March 18,384 17,007 16,163 17,631 17,339 16,456 April 19,837 17,870 15,504 14,950 14,543 14,533 May 17,547 16,597 15,473 16,250 16,177 17,325 June 16,694 16,623 14,745 15,508 15,686 17,343Let X1 and X2 be independent random variables having the standard normal distribution. Obtain the joint Lebesgue density of (Y1, Yz), where Yi = VX?+ X} and Y2 = X1/X2. Are Y1 and Y2 independent? Note. For this type of problem, we may apply the following result. Let X be a random k-vector with a Lebesgue density fx and let Y = g(X), where g is a Borel function from (R*, B* ) to (R*, B*). Let A1, . .., Am, be disjoint sets in B* such that R* - (Aj U . . . U Am,) has Lebesgue measure 0 and g on A; is one-to-one with a nonvanishing Jacobian, i.e., the determinant Det(Og(x)/Or) # 0 on Aj, j =1. .... m. Then Y has the following Lebesgue density: fy (x) = >Det (Oh, (x)/ar) | fx (h,(r)). j=1 where h, is the inverse function of g on A;, j = 1, ..., m