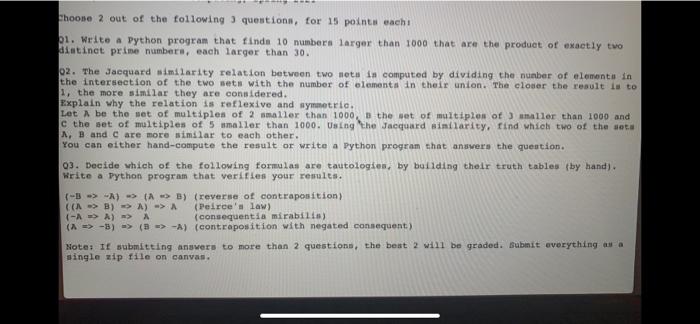
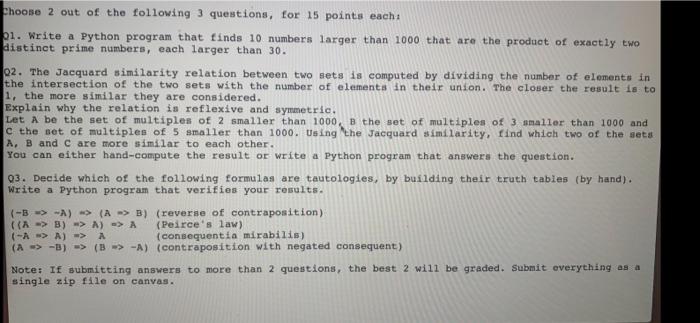
shoone 2 out of the following questions, for 15 points cachi 1. Write a Python program that finds 10 numbers larger than 1000 that are the product of exactly to distinct prime numbers, each larger than 30. 02. The Jacquard similarity relation between two leta in computed by dividing the number of elements in the intersection of the two sets with the number of elements in their union. The closer the result is to 1, the more similar they are considered. Explain why the relation is reflexive and symmetrie. Lot be the set of multiples of 2 smaller than 1000, the set of multiples of smaller than 1000 and e the set of multiples of 5 smaller than 1000. Using the Jacquard similarity, find which two of the sota A, B and C are more similar to each other. You can either hand-compute the result or write a Python program that ansvers the question. 03. Decide which of the following formulas are tautologies, by building their truth tables (by hand). Write a Python program that verifies your results. (-3 > -A) (A > B) (reverse of contraposition) CO > B) > A) -> A (Peirce's law) (-A-A) - A (consequentia mirabilis) (4 => -)-> (a -> -A) (contraposition with negated consequent) Note: If submitting answers to more than 2 questions, the best 2 will be graded. Submit everything as a single zip file on canvas. Choose 2 out of the following 3 questions, for 15 points each 21. Write a Python program that finds 10 numbers larger than 1000 that are the product of exactly two distinct prime numbers, each larger than 30. 02. The Jacquard similarity relation between two sets is computed by dividing the number of elements in the intersection of the two sets with the number of elements in their union. The closer the result is to 1, the more similar they are considered. Explain why the relation is reflexive and symmetric. Let A be the set of multiples of 2 smaller than 1000, B the set of multiples of 3 smaller than 1000 and c the set of multiples of 5 smaller than 1000. Using the Jacquard similarity, find which two of the sets A, B and C are more similar to each other. You can either hand-compute the result or write a Python program that answers the question. 03. Decide which of the following formulas are tautologies, by building their truth tables (by hand). Write a Python program that verifies your results. (-B => -A) (A -> B) (reverse of contraposition) ((A-> B)-> A) => A (Peirce's law) (-A-> A) => A (consequentia mirabilis) (A -> -3) => (B -> -A) (contraposition with negated consequent) Note: If submitting answers to more than 2 questions, the best 2 will be graded. Submit everything as a single zip file on canvas