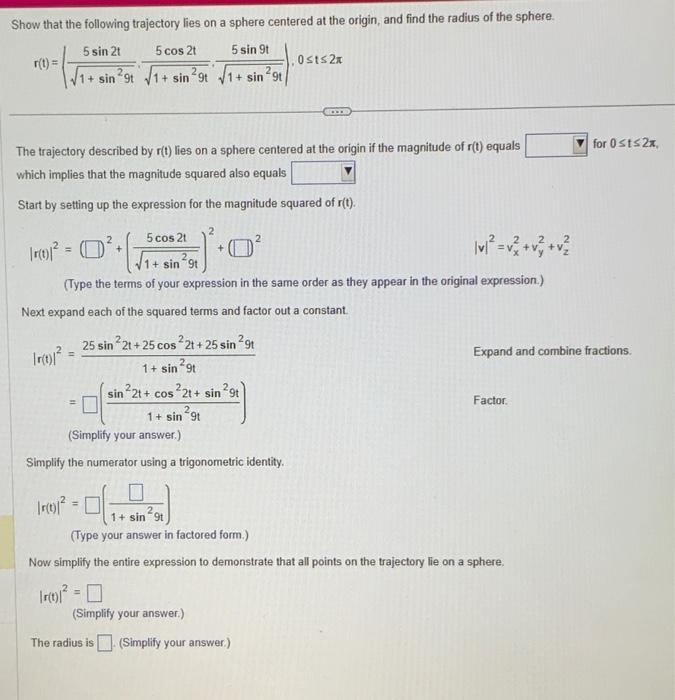
Show that the following trajectory lies on a sphere centered at the origin, and find the radius of the sphere. 5 sin 2t 5 cos 2t 5 sin 9t 2 1+ sin29t 1+ sin 29t 1+ sin9t r(t) = The trajectory described by r(t) lies on a sphere centered at the origin if the magnitude of r(t) equals which implies that the magnitude squared also equals Start by setting up the expression for the magnitude squared of r(t). |1|0(0)1 = 0. [ [r(t)/ \v = + + 1+ sin 9t (Type the terms of your expression in the same order as they appear in the original expression.) Next expand each of the squared terms and factor out a constant. = 5 cos 21 25 sin 2t+25 cos 2t+ 25 sin 9t 2. 1+ sin 9t sin 22t+ cos22t+ sin 9t 2 1+ sin 9t (Simplify your answer.) Simplify the numerator using a trigonometric identity. |r0| = 0 0st2* 1r01 = 0 (Simplify your answer.) The radius is. (Simplify your answer.) 1+ sin 9t (Type your answer in factored form.) Now simplify the entire expression to demonstrate that all points on the trajectory lie on a sphere. Expand and combine fractions. Factor. for 0ts 2x,