Barry Simkin’s Hardware store sells the Ace model electric drill. Daily demand for the drill is relatively low but subject to some variability. Over the past 300 days, Simkin has observed the demand frequency shown in column 2 of Table 1 below. He converts this historical frequency into a probability distribution for the variable daily demand (column 3).

When Simkin places an order to replenish his inventory of drills, the time between when he places an order and when it is received (i.e. the lead time) is a probabilistic variable. Based on the past 100 orders, Simkin has found the lead time follows a discrete uniform distribution between one and three days. That is,

Lead time (days)	Probability
1 2 3	1/3 1/3 1/3

He currently has seven (7) Ace electric drills in stock, and there are no orders due.

Simkin wants to identify the order quantity: Q and reorder point: R that will help him reduce his total monthly costs. The order quantity is the fixed size of each order that is placed. If the inventory level at the end of a day is at or below the reorder point R, an order is placed. The total cost includes the following components:

A fixed ordering cost that is incurred each time an order is placed.

A holding cost for each drill held in inventory from one period to the next.

A stockout cost for each drill that is not available to satisfy demand in a particular day.

Simkin estimates that the fixed cost of placing an order with his Ace drill supplier is $20. The cost of holding a drill in stock is $0.50 per drill per month. Assuming the shop operates 25 days each month on average, this translates to a holding cost of $0.02 per drill per day. Each time Simkin is unable to satisfy a demand (i.e., he has a stockout), the customer buys the drill elsewhere, and Simkin loses the sale. He estimates that the cost of a stockout is $8 per drill.

Note that there are two decision variables (order quantity, Q, and reorder point, R) and two probabilistic components (demand and lead time) in Simkin’s inventory problem. Using simulation, we can try different (Q, R) combinations (or policies) to see which combination yields the lowest total cost. Set up an Excel simulation model that will help SHS estimate the total cost for an inventory policy that has Q = 10 and R = 5; that is, each time the inventory position at the end of the day drops to five or fewer, we place an order for 10 drills with supplier. Simulate 100 days of operation. Your simulation should keep track of the following quantities: Beginning inventory, units received, available inventory, demand filled, ending inventory, stockouts, whether an order is placed or not, lead time and when the order arrives. Follow the BUTLER inventory problem (section 12.2 page 563) in your textbook.

Table 1: Distribution of Daily Demand for Ace Electric Drills

Demand for Drills	Frequency	Probability
0	15	15/300 = 0.05
1	30	30/300 = 0.10
2	60	60/300 = 0.20
3	120	120/300 = 0.40
4	45	45/300 = 0.15
5	30	30/300 = 0.10
Total	300	300/300 = 1.00

Your simulation should include the information summarized in the following tables (split into 2 tables for convenience). Note: Inventory position = Inventory on hand + Inventory on order (but not yet received). The 2 random inputs are demand and lead time.

A	B	C	D	E	F	G
Day	Beginning inventory	Units received	Available inventory	Demand	Demand filled	Ending inventory
1 2 etc.	7 4 -	0 0 -	7 4 -	3 3 -	3 3 -	4 1 -

H	I	J	K	L	M	N	O
Stockout	Inventory position	Place order? Yes =1; No = 0	Lead time	Order arrive on day	Inventory cost	Stockout cost	Order cost
0 0 etc.	4 11 -	1 0 -	2 0 -	4 0 -	$0.08 $0.02 -	$0 $0 -	$20 $0 -
				Total
				Total monthly cost

Note: The numbers in the above tables are shown as examples and may not be the same in your spreadsheet simulation.

Please shown how to use excel solve question, For each spreadsheet, show only the first five and last five trials of your simulation. For example, if the number of simulation trials required is 1000, show only trials 1 to 5 and 996 to 1000 by hiding the intermediate trials from 6 to 995.

 

 

 

 

 

  

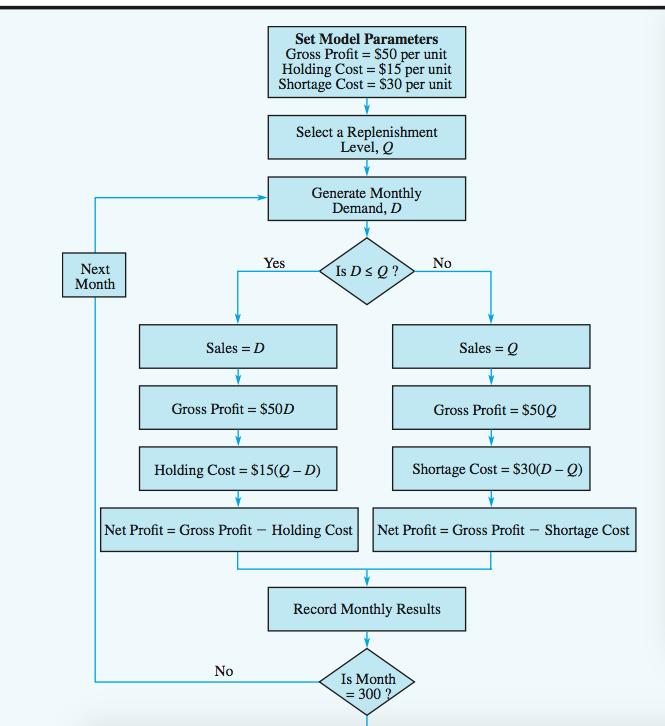
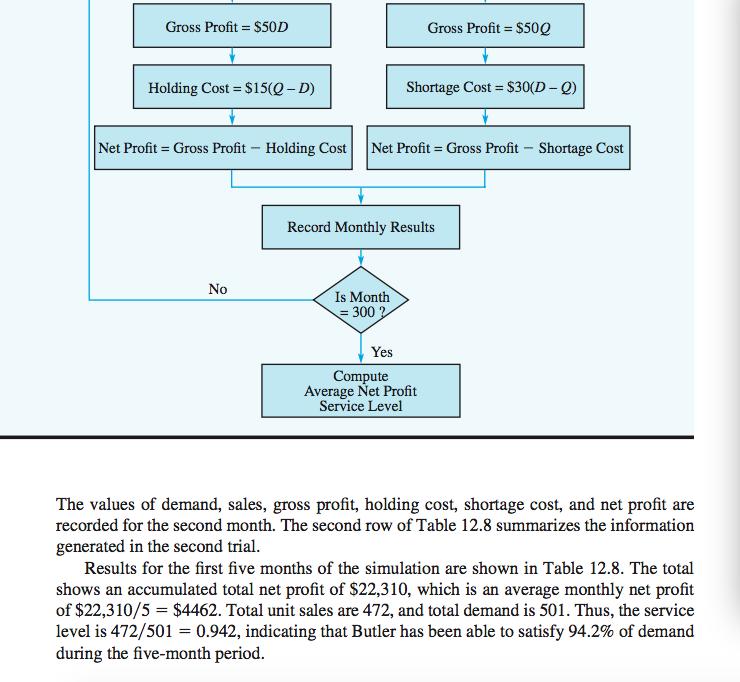
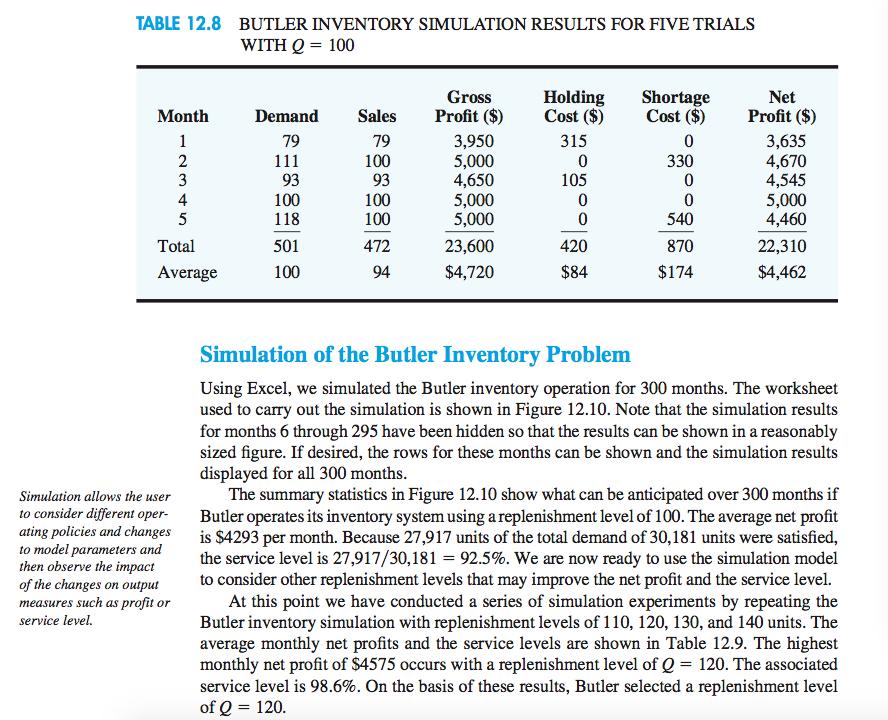
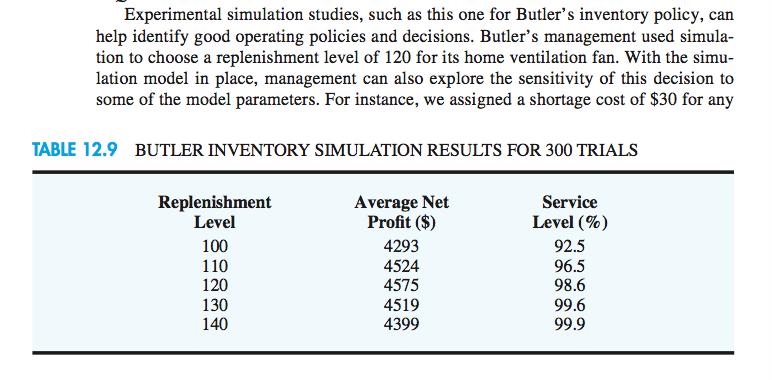
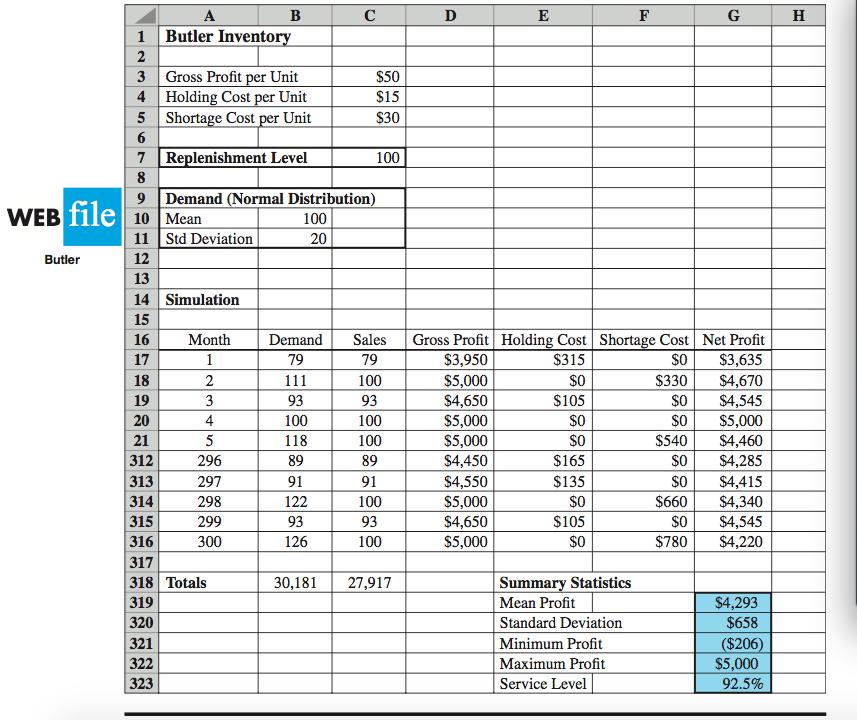
12.2 INVENTORY SIMULATION In this section we describe how simulation can be used to establish an inventory policy for a product that has an uncertain demand. The product is a home ventilation fan distributed by the Butler Electrical Supply Company. Each fan costs Butler $75 and sells for $125. Thus Butler realizes a gross profit of $125 $75 = $50 for each fan sold. Monthly demand for the fan is described by a normal probability distribution with a mean of 100 units and a standard deviation of 20 units. Butler receives monthly deliveries from its supplier and replenishes its inventory to a level of Q at the beginning of each month. This beginning inventory level is referred to as the replenishment level. If monthly demand is less than the replenishment level, an inventory holding cost of $15 is charged for each unit that is not sold. However, if monthly demand is greater than the replenishment level, a stock-out occurs and a shortage cost is incurred. Because Butler assigns a goodwill cost of $30 for each customer turned away, a shortage cost of $30 is charged for each unit of demand that cannot be satisfied. Manage- ment would like to use a simulation model to determine the average monthly net profit resulting from using a particular replenishment level. Management would also like infor- mation on the percentage of total demand that will be satisfied. This percentage is referred to as the service level. The controllable input to the Butler simulation model is the replenishment level, Q. The uncertain input is the monthly demand, D. The two output measures are the average monthly net profit and the service level. Computation of the service level requires that we keep track of the number of fans sold each month and the total demand for fans for each month. The service level will be computed at the end of the simulation run as the ratio of total units sold to total demand. A diagram of the relationship between the inputs and the outputs is shown in Figure 12.8.