Slide 24: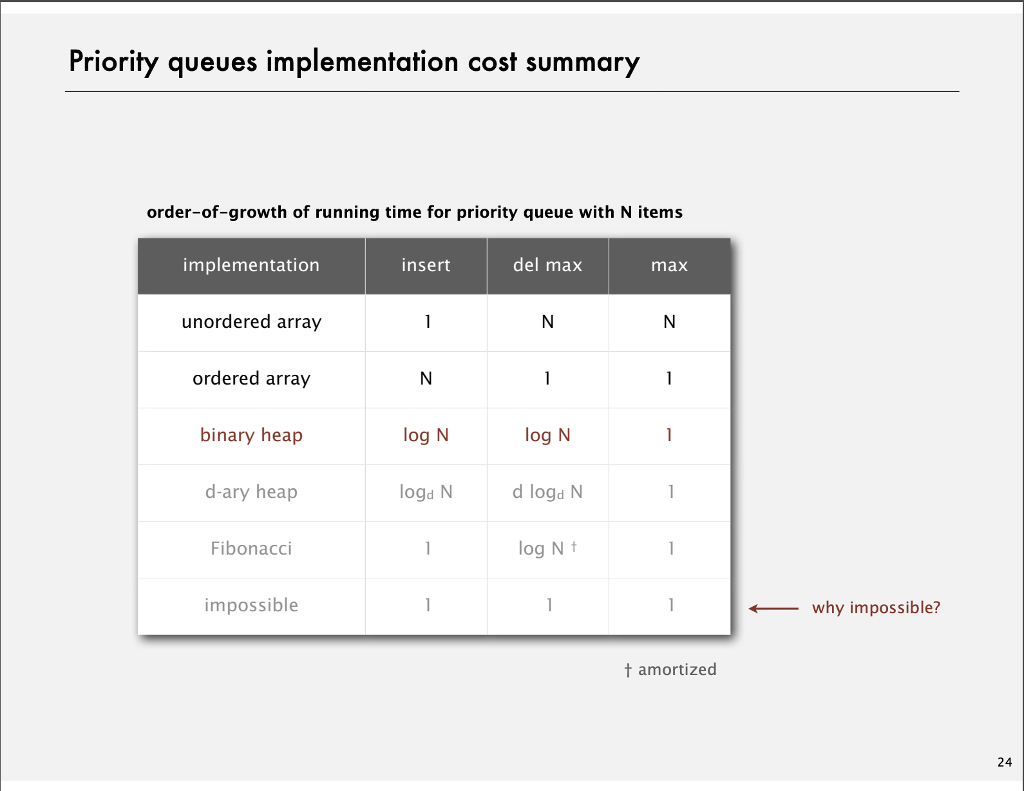
Slide 38: 
Slide 39: 
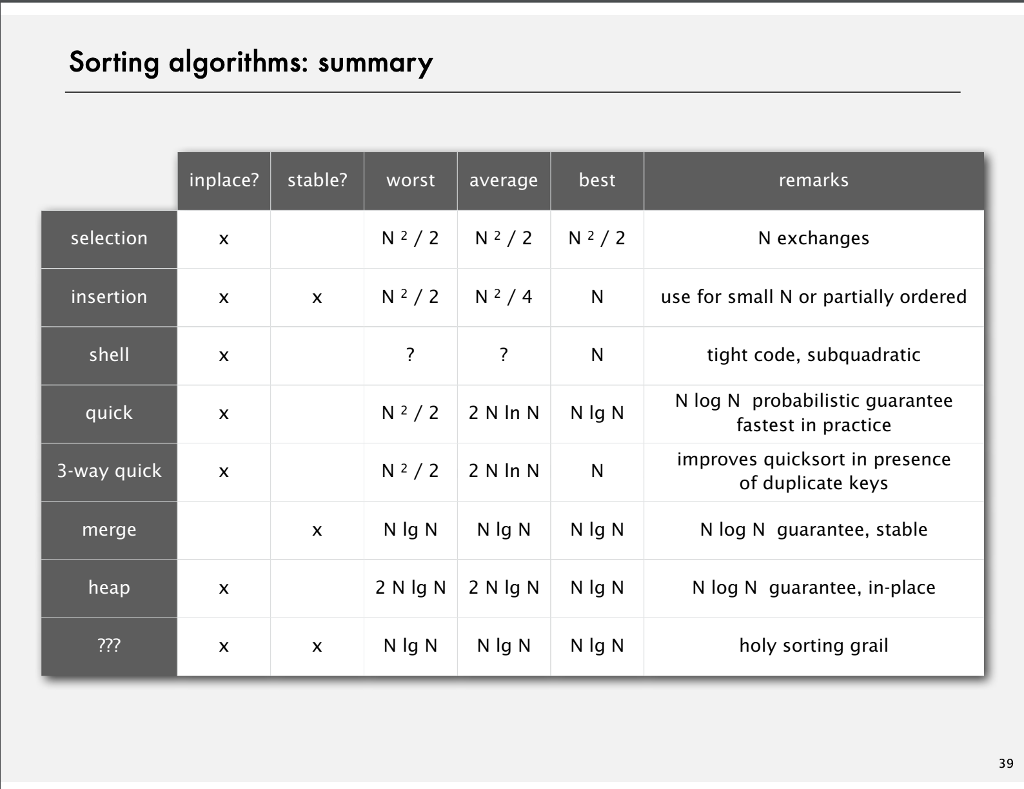
1. Priority Queues -In the slides and lecture, we talked about binary heaps, a data structure where the only constant order to maintain is that the parent is either larger (max-heap) or smaller (min-heap) than its two children. On Slide 24 of Priority Queues, they list two other data structures: the d-ary heap and the Fibonacci heap. In this problem, we want to implement the max d-ary heap. A d-ary heap is a heap data structure that allows for more than two children per parent node with the rule that the parent node must always be larger than the child node. You will implement this using arrays internally, storing only integers inside. The functions are DaryHeap(int d); -- Constructor to create the DaryHeap, where 'd' is the number of children allowed a. b. Void insert(int k); - Adds an integer 'k' into the DaryHeap in proper place. Note: you will need to properly balance the heap in the event of the child being larger than the parent. As such, implement this method a. i. swim(int k); - Promotes a child further up the heap structure until it is in proper order. Typically done by swapping with the parent Int delMax(); - - Swap the largest value in the heap with the most recent child, and then delete that largest value from the heap. Return the largest value to the user. c. Note: you will need to properly balance the heap after deletion. Implement the method: a. i. Sink(int k) - Demotes a parent node down the heap structure through swaps until it is in final order. Make sure that the heap structure is preserved once the method is completed (max heap condition) d. Int[] sortedArray daryHeapsort(); - Returns the contents of the heap in sorted order implementing heapsort e. Inside your heap, begin with an array of constant size '10'. When the values inserted into the heap exceed size 10, implement this method a. doubleArray); -- Double the internal array inside the heapsort in the event that it becomes too large. Do this by instantiating an array of size 2N and copying the values over. f. Include a PDF, Problem1.PDF, where you give a short explanation as to what the Big- O time complexity of the delMax(); and daryHeapsort(); functions are in the worst case. Please include leading coefficients, if any. If there is a constant, say 3*N, please show that. If the constant is a variable, list the variable in your O() function. Look at the heapsort on slide 39 for an example. Your proof is up to you, detailed mathematics is not required. Please highlight in your code where the time complexity of the operations occur from. Reference slides 24, 38, 39 for ideas on what this might be 1. Priority Queues -In the slides and lecture, we talked about binary heaps, a data structure where the only constant order to maintain is that the parent is either larger (max-heap) or smaller (min-heap) than its two children. On Slide 24 of Priority Queues, they list two other data structures: the d-ary heap and the Fibonacci heap. In this problem, we want to implement the max d-ary heap. A d-ary heap is a heap data structure that allows for more than two children per parent node with the rule that the parent node must always be larger than the child node. You will implement this using arrays internally, storing only integers inside. The functions are DaryHeap(int d); -- Constructor to create the DaryHeap, where 'd' is the number of children allowed a. b. Void insert(int k); - Adds an integer 'k' into the DaryHeap in proper place. Note: you will need to properly balance the heap in the event of the child being larger than the parent. As such, implement this method a. i. swim(int k); - Promotes a child further up the heap structure until it is in proper order. Typically done by swapping with the parent Int delMax(); - - Swap the largest value in the heap with the most recent child, and then delete that largest value from the heap. Return the largest value to the user. c. Note: you will need to properly balance the heap after deletion. Implement the method: a. i. Sink(int k) - Demotes a parent node down the heap structure through swaps until it is in final order. Make sure that the heap structure is preserved once the method is completed (max heap condition) d. Int[] sortedArray daryHeapsort(); - Returns the contents of the heap in sorted order implementing heapsort e. Inside your heap, begin with an array of constant size '10'. When the values inserted into the heap exceed size 10, implement this method a. doubleArray); -- Double the internal array inside the heapsort in the event that it becomes too large. Do this by instantiating an array of size 2N and copying the values over. f. Include a PDF, Problem1.PDF, where you give a short explanation as to what the Big- O time complexity of the delMax(); and daryHeapsort(); functions are in the worst case. Please include leading coefficients, if any. If there is a constant, say 3*N, please show that. If the constant is a variable, list the variable in your O() function. Look at the heapsort on slide 39 for an example. Your proof is up to you, detailed mathematics is not required. Please highlight in your code where the time complexity of the operations occur from. Reference slides 24, 38, 39 for ideas on what this might be
