Question
Small effect sizes can make a big difference ~ Suppose a test is used to select applicants for a job advancement program. Assume that there
Small effect sizes can make a big difference ~ Suppose a test is used to select applicants for a job advancement program.
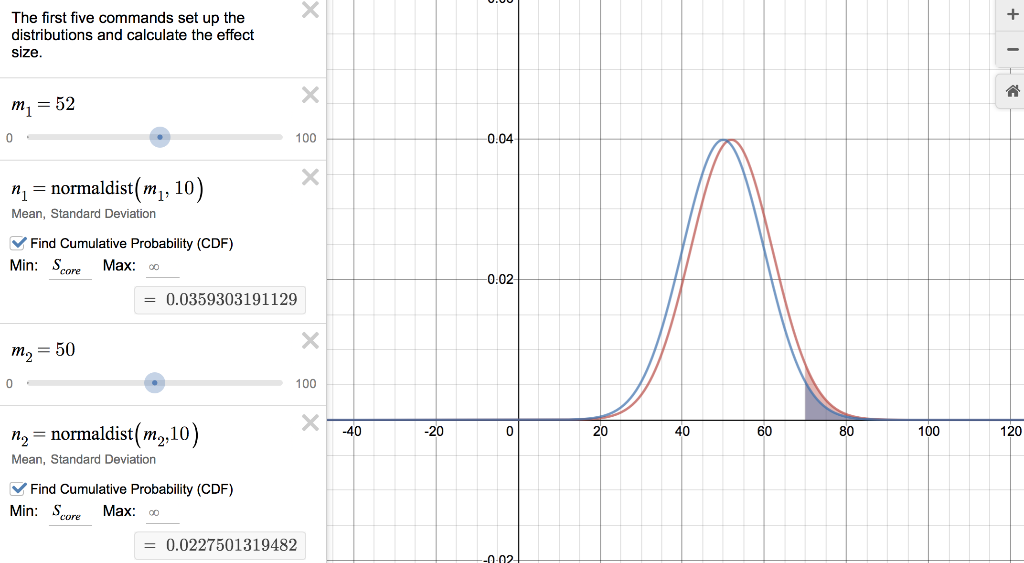
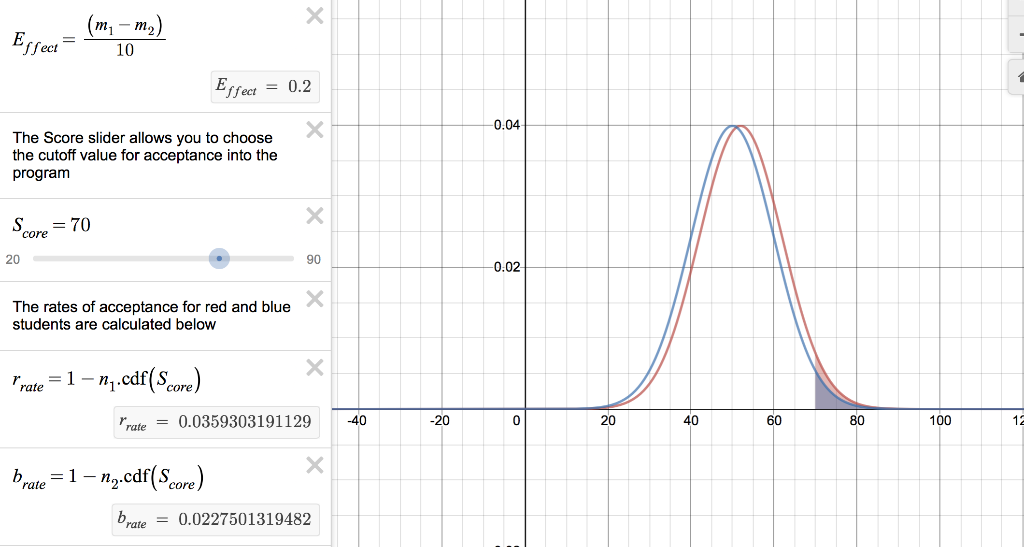
Assume that there are two types of applicants (red and blue) and that the mean for the red applicants is 52, the mean for the blue applicants is 50, both distributions are nearly normal, and the standard deviation for each distribution is 10. The difference in means (that is, the effect size) is therefore only 0.2 standard deviations and the effect of being either red or blue would be considered small, not visible to the naked eye.
At one large company there are two programs that use this test to screen applicants.
Program 1 is less selective. Managers use a cutoff value of 40 for this program, meaning that any applicant who scores higher than 40 is accepted into the program.
Program 2 is very selective. Managers use a cutoff value of 70 for Program 2, meaning that only applicants who score higher than 70 are accepted into the program.
Task 1
You can use this Desmos graph page to help you answer questions 1-4 and question 7. Write a paragraph or two that summarizes your findings and explains your recommendation to the program managers.
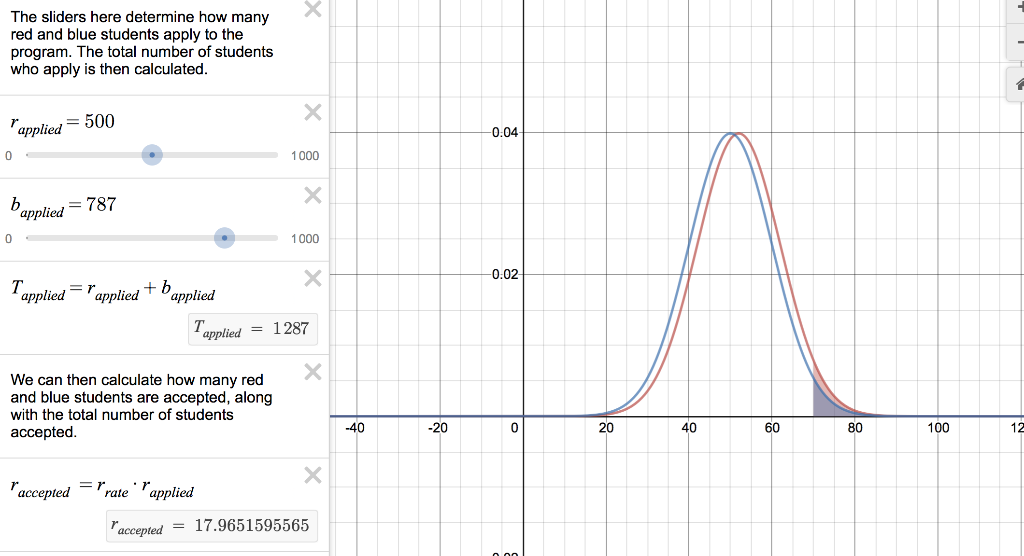
- If 500 red applicants and 500 blue applicants apply for Program 1, how many red applicants are accepted and how many blue applicants are accepted?
- What proportion of the total number of accepted applicants are red? What proportion are blue?
- If 500 red applicants and 500 blue applicants apply for Program 2, how many red applicants are accepted and how many blue applicants are accepted?
- What proportion of the total number of accepted applicants are red? What proportion are blue?
- Do you think this test appears to unfairly privilege red applicants over blue applicants for Program 1?
- Do you think this test appears to unfairly privilege red applicants over blue applicants for Program 2?
- Suppose managers wanted to have equal proportion of red and blue applicants accepted into their programs. Experiment by changing the number of applicants for each group to see what it would take to achieve equal proportions, then make a recommendation to the program leaders about using this test to screen applicants.
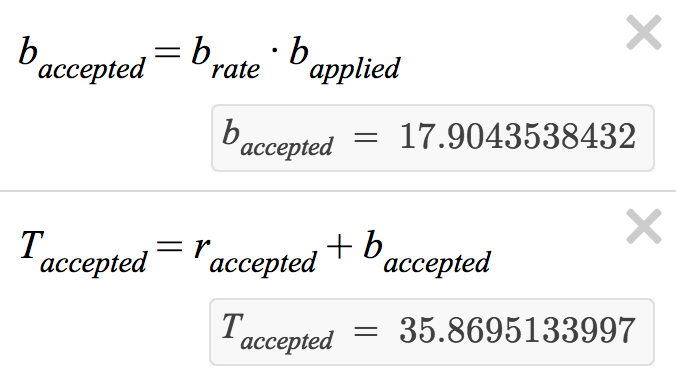
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


