So I submitted for someone to fix my code on here, to fix the physics of my code but they kind of broke my code because now when I move the mallet towards the puck it just throws me with errors and I don't know how to fix it. And because of this, I don't even know if they did fix the physics in my code.

This is what I asked them to do:

please fix the physics. My teacher said that my physics is a bit wrong in the way that the mallets are square instead of a circle. For example, sometimes when the puck goes behind the user's mallet, it just completely goes through the mallet when it should naturally bounce off of it. It's mainly a radius issue, the code fully works, it's just a physics issue.

Below is a drawn example he drew out showing what the current physics is and what it should be. The dot represents the radius.

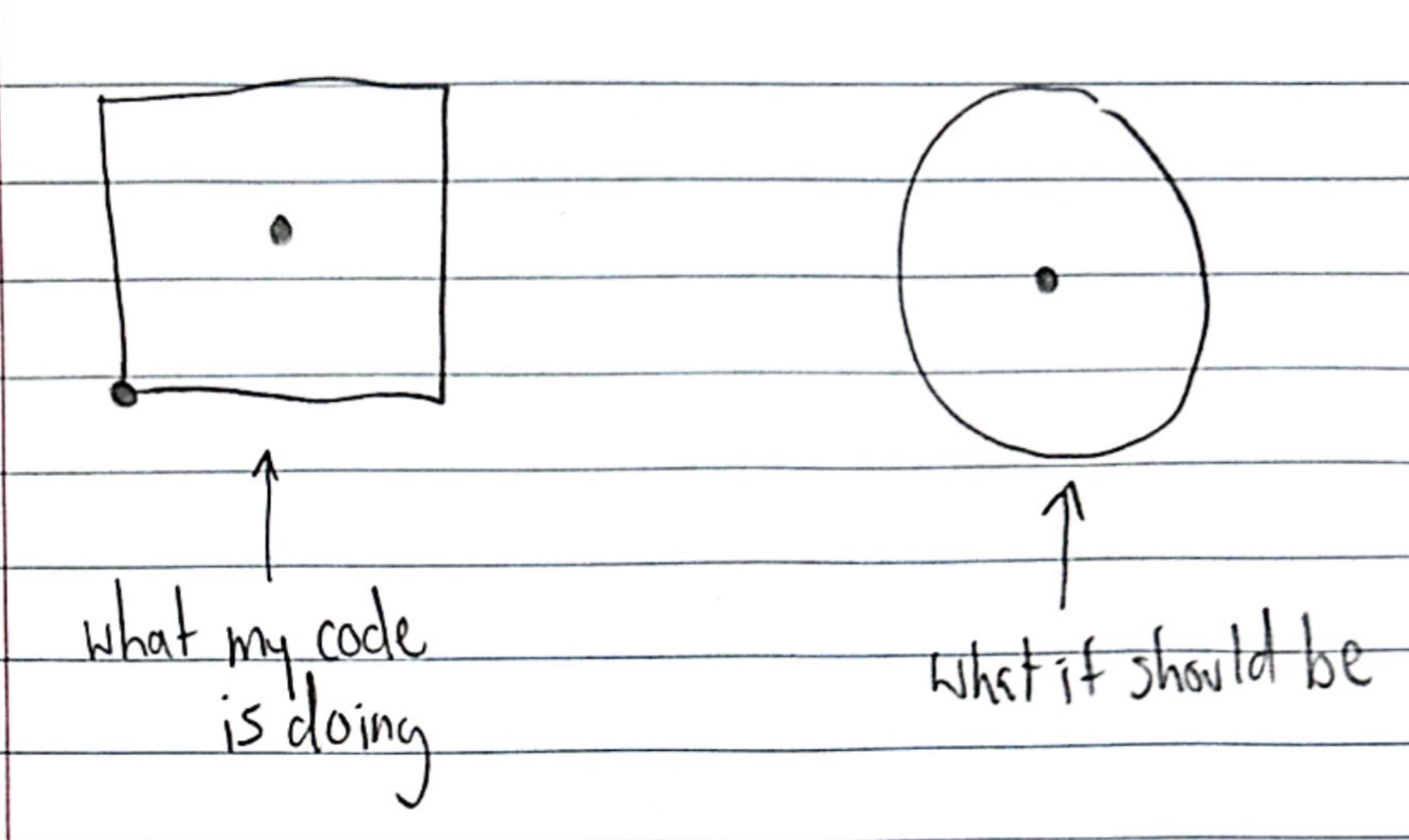
ill provide the code they fixed and also my original code (MATLAB CODE)

fixed:

function air_hockey_rink()

fig = figure('Name', 'Air Hockey', 'NumberTitle', 'off', 'KeyPressFcn', @keypress_callback);

ax = axes('XLim', [0, 100], 'YLim', [0, 50], 'Position', [0, 0, 1, 1]);

axis off; hold on; axis equal;

rectangle('Position', [10, 5, 80, 40], 'EdgeColor', 'b', 'LineWidth', 2, 'FaceColor', 'w');

line([50, 50], [5, 45], 'Color', 'k', 'LineWidth', 2);

circleRadius = 5;

circleDiameter = circleRadius * 2;

circleX = 50 - circleRadius;

circleY = 25 - circleRadius;

rectangle('Position', [circleX, circleY, circleDiameter, circleDiameter], 'Curvature', [1, 1], 'EdgeColor', 'k', 'LineWidth', 2);

goalWidth = 12;

rectangle('Position', [10, 20, 3, goalWidth], 'EdgeColor', 'b', 'FaceColor', 'b');

rectangle('Position', [87, 20, 3, goalWidth], 'EdgeColor', 'r', 'FaceColor', 'r');

userMallet = rectangle('Position', [20, 25, 6, 6], 'Curvature', [1, 1], 'FaceColor', 'b');

oppMallet = rectangle('Position', [75, 25, 6, 6], 'Curvature', [1, 1], 'FaceColor', 'r');

puck = rectangle('Position', [47.5, 22.5, 5, 5], 'Curvature', [1, 1], 'FaceColor', [0.5, 0.5, 0.5]);

user_Score = 0;

opp_Score = 0;

scoreText = text(50, 2, 'Score: 0 - 0', 'HorizontalAlignment', 'center', 'FontSize', 14, 'FontWeight', 'bold');

malletSpeed = 2;

puckSpeed = [0, 0];

puckState = 'stationary';

oppDirection = 1;

oppSpeed = 0.75;

function keypress_callback(~, event)

switch event.Key

case 'leftarrow'

userMallet.Position(1) = max(userMallet.Position(1) - malletSpeed, 10);

case 'rightarrow'

rightBoundary = 50 - userMallet.Position(3);

newPosX = min(userMallet.Position(1) + malletSpeed, rightBoundary);

userMallet.Position(1) = newPosX;

case 'uparrow'

userMallet.Position(2) = min(userMallet.Position(2) + malletSpeed, 40);

case 'downarrow'

userMallet.Position(2) = max(userMallet.Position(2) - malletSpeed, 5);

end

end

while ishandle(fig)

% Update puck position if it's 'moving'

if strcmp(puckState, 'moving')

puck.Position(1:2) = puck.Position(1:2) + puckSpeed;

end

% Collision with walls

if puck.Position(1) = 85

puckSpeed(1) = -puckSpeed(1);

end

if puck.Position(2) = 40

puckSpeed(2) = -puckSpeed(2);

end

% Move opponent mallet up and down

oppMallet.Position(2) = oppMallet.Position(2) + oppSpeed * oppDirection;

if oppMallet.Position(2) = 40

oppDirection = -oppDirection;

end

% Collision with user mallet

if strcmp(puckState, 'moving') || strcmp(puckState, 'stationary')

if isCollisionDetected(puck, userMallet)

% Trigger a bounce off the user's mallet

[puckSpeed, ~] = handleMalletCollision(puck, userMallet);

puckState = 'moving';

end

end

% Collision with opponent mallet

if isCollisionDetected(puck, oppMallet)

% Trigger a bounce off the opponent's mallet

[puckSpeed, ~] = handleMalletCollision(puck, oppMallet);

puckState = 'moving';

end

% Goal detection

if puck.Position(1) 20 && puck.Position(2)

opp_Score = opp_Score + 1;

resetPuck();

elseif puck.Position(1) >= 82 && puck.Position(2) > 20 && puck.Position(2)

user_Score = user_Score + 1;

resetPuck();

end

% Update score display

scoreText.String = sprintf('Score: %d - %d', user_Score, opp_Score);

% Pause

pause(0.03);

end

end

function resetPuck()

if user_Score > opp_Score

puck.Position = [75, 25, 5, 5]; % Place the puck near the opponent

else

puck.Position = [25, 25, 5, 5]; % Place the puck near the player

end

puckSpeed = [0, 0]; % Puck is still until hit by the mallet

puckState = 'stationary';

end

function isColliding = isCollisionDetected(puck, mallet)

distance = sqrt((puck.Position(1) + puck.Position(3)/2 - (mallet.Position(1) + mallet.Position(3)/2))^2 + ...

(puck.Position(2) + puck.Position(4)/2 - (mallet.Position(2) + mallet.Position(4)/2))^2);

isColliding = distance

end

function [newVp, newVb] = handleMalletCollision(puck, mallet)

xp1 = puck.Position(1) + puck.Position(3)/2; % Puck center x

yp1 = puck.Position(2) + puck.Position(4)/2; % Puck center y

Vp1 = puckSpeed;

xb1 = mallet.Position(1) + mallet.Position(3)/2; % Mallet center x

yb1 = mallet.Position(2) + mallet.Position(4)/2; % Mallet center y

Vb1 = [0, 0]; % Mallet is stationary

rp = puck.Position(3)/2; % Puck radius

rb = mallet.Position(3)/2; % Mallet radius

% calculate angles for collision

theta = -atan2(yb1 - yp1, xb1 - xp1);

alpha = atan2(Vb1(2), Vb1(1));

beta = atan2(Vp1(2), Vp1(1));

% Remove any overlap between puck and blocker

xp2 = xb1 - (rp + rb) * cos(theta);

yp2 = yb1 + (rp + rb) * sin(theta);

% calculate normal and tangential components of velocity before collision

Vb1n = Vb1_mag * cos(theta + alpha);

Vb1s = Vb1_mag * sin(theta + alpha);

Vp1n = Vp1_mag * cos(theta + beta);

Vp1s = Vp1_mag * sin(theta + beta);

% masses of puck and mallet

mp = puck.mass;

mb = mallet.mass;

% total momentum and kinetic energy before the collision

P1n = mp * Vp1n + mb * Vb1n;

KE1 = 0.5 * mp * Vp1_mag^2 + 0.5 * mb * Vb1_mag^2;

% coefficients for the quadratic equation

a = mp^2 + mp * mb / mb;

b = -2 * P1n * mp / mb;

c = P1n^2 / mb + mp * Vp1s^2 + mb * Vb1s^2 - 2 * KE1;

% solve the quadratic equation for Vp2n

Vp2n = (-b - sqrt(b^2 - 4 * a * c)) / (2 * a);

% new velocity of the blocker in the normal direction

Vb2n = (P1n - mp * Vp2n) / mb;

% new velocities in the tangential direction

Vp2s = Vp1s;

Vb2s = Vb1s;

% calculate the final speeds and angles

Vp2_mag = sqrt(Vp2n^2 + Vp2s^2);

beta2 = atan2(Vp2s, Vp2n) - theta;

Vb2_mag = sqrt(Vb2n^2 + Vb2s^2);

alpha2 = atan2(Vb2s, Vb2n) - theta;

% convert back to x and y components

newVp = [Vp2_mag * cos(beta2), Vp2_mag * sin(beta2)];

newVb = [Vb2_mag * cos(alpha2), Vb2_mag * sin(alpha2)];

end

original code:

function air_hockey_rink()

% figure and axes

fig = figure('Name', 'Air Hockey', 'NumberTitle', 'off', 'KeyPressFcn', @keypress_callback);

ax = axes('XLim', [0, 100], 'YLim', [0, 50], 'Position', [0, 0, 1, 1]);

axis off; hold on; axis equal;

% rink definitions

rectangle('Position', [10, 5, 80, 40], 'EdgeColor', 'b', 'LineWidth', 2, 'FaceColor', 'w');

% middle line definition

line([50, 50], [5, 45], 'Color', 'k', 'LineWidth', 2);

% Circle in the middle of the rink

circleRadius = 5; % Set the radius of the circle

circleDiameter = circleRadius * 2;

circleX = 50 - circleRadius; % X position

circleY = 25 - circleRadius; % Y position

rectangle('Position', [circleX, circleY, circleDiameter, circleDiameter], 'Curvature', [1, 1], 'EdgeColor', 'k', 'LineWidth', 2);

% goal definitions

goalWidth = 12;

rectangle('Position', [10, 20, 3, goalWidth], 'EdgeColor', 'b', 'FaceColor', 'b');

rectangle('Position', [87, 20, 3, goalWidth], 'EdgeColor', 'r', 'FaceColor', 'r');

% mallets and puck

userMallet = rectangle('Position', [20, 25, 6, 6], 'Curvature', [1, 1], 'FaceColor', 'b');

oppMallet = rectangle('Position', [75, 25, 6, 6], 'Curvature', [1, 1], 'FaceColor', 'r');

puck = rectangle('Position', [47.5, 22.5, 5, 5], 'Curvature', [1, 1], 'FaceColor', [0.5, 0.5, 0.5]);

% scores

user_Score = 0;

opp_Score = 0;

% score board

scoreText = text(50, 2, 'Score: 0 - 0', 'HorizontalAlignment', 'center', 'FontSize', 14, 'FontWeight', 'bold');

% movement variables

malletSpeed = 2;

puckSpeed = [0, 0]; % initial speed in x and y directions

puckState = 'stationary'; % puck is still

% opponent movement

oppDirection = 1; % 1 for right, -1 for left

oppSpeed = 0.75; % speed of the opponent's mallet

% keypress_callback function

function keypress_callback(~, event)

switch event.Key

case 'leftarrow'

% prevent moving left beyond the left boundary

userMallet.Position(1) = max(userMallet.Position(1) - malletSpeed, 10);

case 'rightarrow'

% calculate the right boundary for the mallet

rightBoundary = 50 - userMallet.Position(3); % prevent from crossing middle line

newPosX = min(userMallet.Position(1) + malletSpeed, rightBoundary);

userMallet.Position(1) = newPosX;

case 'uparrow'

userMallet.Position(2) = min(userMallet.Position(2) + malletSpeed, 40);

case 'downarrow'

userMallet.Position(2) = max(userMallet.Position(2) - malletSpeed, 5);

end

end

% main game loop

while ishandle(fig)

% update puck position if it's 'moving'

if strcmp(puckState, 'moving')

puck.Position(1:2) = puck.Position(1:2) + puckSpeed;

end

% collision with walls

if puck.Position(1) = 85

puckSpeed(1) = -puckSpeed(1);

end

if puck.Position(2) = 40

puckSpeed(2) = -puckSpeed(2);

end

% move opponent mallet up and down

oppMallet.Position(2) = oppMallet.Position(2) + oppSpeed * oppDirection;

if oppMallet.Position(2) = 40

oppDirection = -oppDirection;

end

% collision with usermallet

if strcmp(puckState, 'moving') || strcmp(puckState, 'stationary')

if abs(puck.Position(1) - userMallet.Position(1))

abs(puck.Position(2) - userMallet.Position(2))

puckSpeed = [1,-1];

puckState = 'moving';

end

end

% collision with oppmallet

if abs(puck.Position(1) - oppMallet.Position(1))

abs(puck.Position(2) - oppMallet.Position(2))

% trigger a bounce off the opponent's mallet

puckSpeed = [-1, randi([-1,1])];

puckState = 'moving';

end

% goal detection

if puck.Position(1) 20 && puck.Position(2)

opp_Score = opp_Score + 1;

resetPuck();

elseif puck.Position(1) >= 82 && puck.Position(2) > 20 && puck.Position(2)

user_Score = user_Score + 1;

resetPuck();

end

% update score display

scoreText.String = sprintf('Score: %d - %d', user_Score, opp_Score);

% pause

pause(0.03);

end

% reset puck

function resetPuck()

% place the puck in front of the user/opponent who was scored upon

if user_Score > opp_Score

% place the puck near the opponent

puck.Position = [75, 25, 5, 5];

else

% place the puck near the player

puck.Position = [25, 25, 5, 5];

end

puckSpeed = [0, 0]; % puck is still until hit by the mallet

puckState = 'stationary';

end

end

% collision detection function

function isColliding = isCollisionDetected(puck, mallet)

distance = sqrt((puck.position.x - mallet.position.x)^2 + (puck.position.y - mallet.position.y)^2);

isColliding = distance

end

% handleMalletCollision function

function [newVp, newVb] = handleMalletCollision(puck, mallet)

% extract position and velocity components of puck and mallet

xp1 = puck.position.x;

yp1 = puck.position.y;

Vp1 = puck.velocity;

Vp1_mag = norm(Vp1);

xb1 = mallet.position.x;

yb1 = mallet.position.y;

Vb1 = mallet.velocity;

Vb1_mag = norm(Vb1);

rp = puck.radius; % puck radius

rb = mallet.radius; % mallet radius

% calculate angles for collision

theta = -atan2(yb1 - yp1, xb1 - xp1);

alpha = atan2(Vb1(2), Vb1(1));

beta = atan2(Vp1(2), Vp1(1));

% Remove any overlap between puck and blocker

xp2 = xb1 - (rp + rb) * cos(theta);

yp2 = yb1 + (rp + rb) * sin(theta);

% calculate normal and tangential components of velocity before collision

Vb1n = Vb1_mag * cos(theta + alpha);

Vb1s = Vb1_mag * sin(theta + alpha);

Vp1n = Vp1_mag * cos(theta + beta);

Vp1s = Vp1_mag * sin(theta + beta);

% masses of puck and mallet

mp = puck.mass;

mb = mallet.mass;

% total momentum and kinetic energy before the collision

P1n = mp * Vp1n + mb * Vb1n;

KE1 = 0.5 * mp * Vp1_mag^2 + 0.5 * mb * Vb1_mag^2;

% coefficients for the quadratic equation

a = mp^2 + mp * mb / mb;

b = -2 * P1n * mp / mb;

c = P1n^2 / mb + mp * Vp1s^2 + mb * Vb1s^2 - 2 * KE1;

% solve the quadratic equation for Vp2n

Vp2n = (-b - sqrt(b^2 - 4 * a * c)) / (2 * a);

% new velocity of the blocker in the normal direction

Vb2n = (P1n - mp * Vp2n) / mb;

% new velocities in the tangential direction

Vp2s = Vp1s;

Vb2s = Vb1s;

% calculate the final speeds and angles

Vp2_mag = sqrt(Vp2n^2 + Vp2s^2);

beta2 = atan2(Vp2s, Vp2n) - theta;

Vb2_mag = sqrt(Vb2n^2 + Vb2s^2);

alpha2 = atan2(Vb2s, Vb2n) - theta;

% convert back to x and y components

newVp = [Vp2_mag * cos(beta2), Vp2_mag * sin(beta2)];

newVb = [Vb2_mag * cos(alpha2), Vb2_mag * sin(alpha2)];

end

% reset puck position after a goal

function resetPuck()

puck.position.x = 50;

puck.position.y = 25;

puck.velocity = [0, 0];

end

what my code is doing What it should be