Solve Gauss Jordan VBA

'Daniel Schmitt Option Explicit Option Base 1

Sub gauss_jordan() Dim A As Variant, b As Variant, MyRange As Variant Dim AugMatrix() As Variant, x() As Double, f As Double Dim i As Integer, j As Integer, k As Integer, n As Integer, m As Integer

A = Application.InputBox("Please select coefficient matrix", Type:=64) b = Application.InputBox("Please select constant vector", Type:=64)

'check if solution exists If Application.WorksheetFunction.MDeterm(A) = 0 Then MsgBox ("Solution does not exist") Exit Sub End If

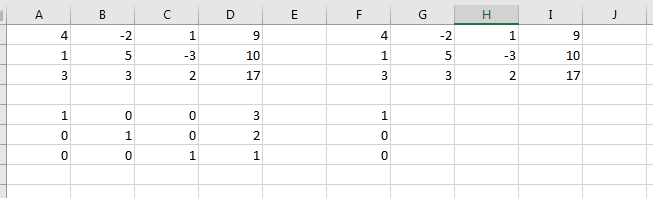
'Define DIM for AugMatrix 'Count how many rows for coefficient matrix A n = UBound(A, 1)

'now define dimensions for augmented matrix and x vector ReDim AugMatrix(n, n + 1), x(n, 1)

For i = 1 To n For j = 1 To n + 1 If j = n + 1 Then AugMatrix(i, j) = b(i, 1) Else AugMatrix(i, j) = A(i, j) End If Next j Next i 'Following checks previous code

Set MyRange = Application.InputBox("Please select cells to output augmented matrix before elimination", Type:=8) MyRange.Value = AugMatrix

'Saves aik value Dim pre_aik As Double

'===========Do elimination Here======== Dim pre_kk As Double For k = 1 To n pre_kk = AugMatrix(k, k) For j = k To n + 1 AugMatrix(k, j) = AugMatrix(k, j) / pre_kk Next j For i = 1 To n If i k Then pre_aik = AugMatrix(i, k) For j = k To n + 1 AugMatrix(i, j) = AugMatrix(i, j) - (pre_aik * AugMatrix(k, j)) Next j Else End If Next i Next k

'Check if elimination is correct

Set MyRange = Application.InputBox("Please select cells to output augmented matrix after elimination", Type:=8) MyRange.Value = AugMatrix

Dim sum_known As Double

'======Do Back substitution here========

'=======================================

Set MyRange = Application.InputBox("Please select cells to output result vector", Type:=8) MyRange.Value = AugMatrix

End Sub

construct a VBA code to implement Gauss elimination method (including back substitution). Your code should be able to solve arbitrary system of linear algebra equations then return the solution x vector to spreadsheet.

Solve Gauss Jordan VBA

907 11 132 H 253 G 413 100 E 907 321 11 D 132 001 253 0-0 413 100 A