Solve only the unsolved questions. No explanation, just the answers, please.
https://docs.google.com/spreadsheets/d/16PecTxMOcR69mf7en8iXXqT8vLsWjv-c/edit#gid=1777994166
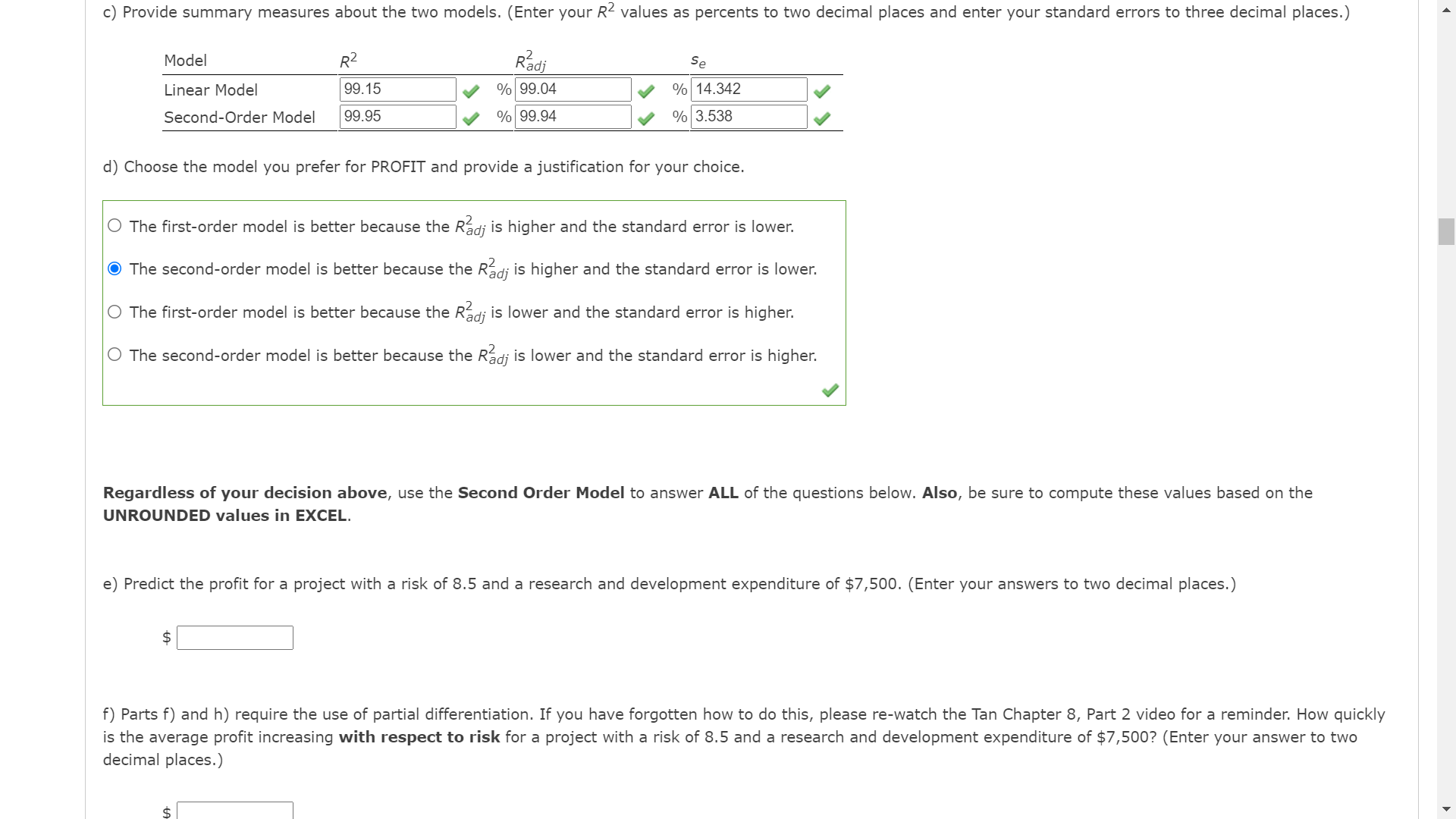
Prot Forecasting: A company is interested in predicting profit for a number of projects based on two explanatory variables: a measure of risk assigned at the outset of the project (x1 = RISK) and the expenditure on research and development for the project (x2 = RD). Data on the three variables PROFIT, RISK, and RD are available in the worksheet entitled RD5. PROFIT is measured in thousands of dollars and RD is measured in hundreds of dollars. Use the data to fit two separate regression models. For the rst model (Linear Model AKA First Order Model), regress PROFIT on the two explanatory variables RISK and RD. (Hint: "Regress PROFIT on X" implies that PROFIT is the y variable and x is the explanatory variable.) a) State the linear model equation. O 37 =130 +51X1 +132X2 +.5'3X2Z O I; = 50 + 31X1 + [32%2 + 193X2 O 9=o +m waxi) 2 o 9=o +31%) +2x2 1 37=o+31X1 +32X2 J However, there is some evidence that the relationship between RD and PROFIT is nonlinear. Therefore, next t the second order polynomial regression model, regress PROFIT on RISK, RD, and RDSQR (the square of the RD variable) as explanatory variables. (Hint: You will have to create the RDSQR variable yourself.) b) State the transformed model equation (i.e., the second order polynomial regression model equation). 37 = [30 + 31M + [32M2 + 3X2 )7 = [30 + 31X1 't 32(Xi2) I7 = 50 + 31X1 + [32X2 57330 +31X1 +132X2 +33X22 9 = 130 + 1(71|)+ 5ng c) Provide summary measures about the two models. (Enter your R2 values as percents to two decimal places and enter your standard errors to three decimal places.) Model R2 Rzadj Se LinearModel l99.15 l; 01499.04 l" 0/ul14342 l; Second-Order Model l99.95 l; U/ol99.94 l,, omlasss l'; d) Choose the model you prefer for PROFIT and provide a justification for your choice. O The first-order model is better because the Rdj is higher and the standard error is lower. The secondorder model is better because the Rgdj is higher and the standard error is lower. 0 The first-order model is better because the Rid]. is lower and the standard error is higher. 0 The second-order model is better because the Rgdj is lower and the standard error is higher. V Regardless of your decision above, use the Second Order Model to answer ALL of the questions below. Also, be sure to compute these values based on the UNROUNDED values in EXCEL. e) Predict the profit for a project with a risk of 8.5 and a research and development expenditure of $7,500. (Enter your answers to two decimal places.) $: f) Parts f) and h) require the use of partial differentiation. If you have forgotten how to do this, please re-watch the Tan Chapter 8, Part 2 video for a reminder: How quickly is the average profit increasing with respect to risk for a project with a risk of 8.5 and a research and development expenditure of $7,500? (Enter your answer to two decimal places.) $ f) Parts f) and h) require the use of partial differentiation. If you have forgotten how to do this, please rewatch the Tan Chapter 8, Part 2 video for a reminder: How quickly is the average profit increasing with respect to risk for a project with a risk of 8.5 and a research and development expenditure of $7,500? (Enter your answer to two decimal places.) $: How quickly is the average profit increasing with respect to research and development expenditure for a project with a risk of 8.5 and a research and development expenditure of $7,500? (Enter your answer to two decimal places.) $: g) Predict the prot for a project with a risk of 6.5 and a research and development expenditure of $9,000. (Enter your answers to two decimal places.) $: h) How quickly is the average profit increasing with respect to risk for a project with a risk of 6.5 and a research and development expenditure of $9,000? (Enter your answer to two decimal places.) $: How quickly is the average profit increasing with respect to research and development expenditure for a project with a risk of 6.5 and a research and development expenditure of $9,000? (Enter your answer to two decimal places.) $