solve please

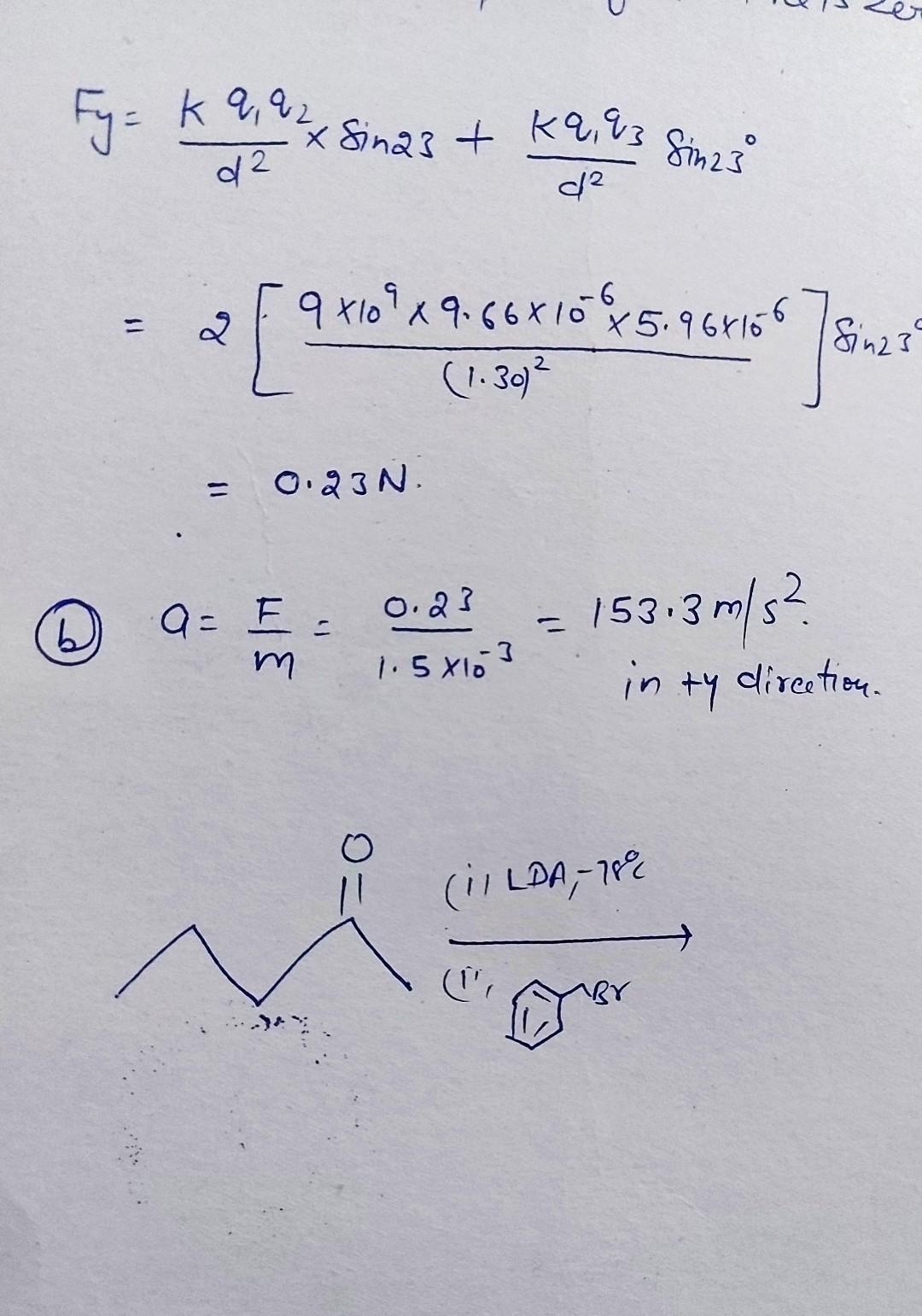
that different sets of 10 as many respectively erived from the quantum-mechanical considerations ch other. It may be mentioned corresponds to the old azimuthal quantum number, k as k = (1 + 1). This gives rise energy levels as shown in Fig. 2.1 for Li atom. For n = 1, 1 = 0 and we expect only a single energy level but as n increases we get values of 1 for each n and an equal number of energy levels. For example, when n = 2,1 = 0 and 1 and we have two energy levels for this principal quantum number. Conventionally the energy levels corresponding to 1 = 0, 1, 2, 3, are denoted by the capital alphabets S, P, D, F,... and the corresponding sub-shells of the electron by small case letters s, p, d, f, These should not be confused with the same letters used above for Rydberg Corrections. Thus, the four sets of energy levels have been shown in the diagram with these letters. The number 2 put as superscript on the left of S, P, D and F shows that these energy levels are doublets which will be discussed later. We can arrive at the above conclusion classically by considering that an alkali atom contains, in addition to the completed subshells of electrons, a single electron in the outermost shell which is called the valence electron. The other electrons in the atom form the core and provide shielding to the nuclear charge. This situation makes the alkali atoms a little different from the hydrogen atom. On account of this fact there is difference between the levels arising from the electrons in the sub-shells s, p, energy d and f for the same total quantum number n due to different magnitude of eccentricity of these orbits and causing decreasing amount of their penetration into the core in the same order (Fig. 2.2). When the electron in an orbit is completely outside the core, the situation is similar to that of the hydrogen atom as for the forbit with n = 4 and I = 3. Burit is much different when the electron is in the s sub-shell for which eccentricity and penetration of the core is maximum. In this case the electron moves under the attractive force of much larger effective nuclear charge for appreciable length of time. For this reason the energy state corresponding to the s orbit lies deepest on the energy scale and is followed by the energy states of p, d and f orbits respectively . In other words the , deviation from the hydrogen terms i.e. the so called Rydberg correction is greater for S terms, smaller for P terms, still smaller for D terms and so on. The Rydberg correction is extremely small for F terms and they are practically terms of the Balmer series of hydrogen atom. On the other hand it is so large for the S terms (for Li it has a value 0.59) that one may not be certain about their true principal quantum number, for example, whether the ground state of Li has n = 1 or 2. apply the selection rules for transitions between the atomic energy levels, any integral value, where n is principal quantum number and Al=+1, where l is alkalis as shown in Fig. 2.1. Evidently, since most of the atoms are expected to lie in quantum number, we can predict the observed series of lines in the spectra of the lowest energy level, i.e. IS, we expect only one series of lines in absorption due to transitions arising from this level, which we call as the Principal series. In emission, however, we expect a series of transitions from 2S, 3S, 4S, ... levels to the relatively low lying 2P level and also a similar series due to transition from 3D, 4D, SD, ... levels to the same 2P level which are called sharp and diffuse series respectively. Transitions from various P levels to IS energy level constitute the Principal series of emission. A set of transitions from 4F, 5F, 6F, ... energy levels to the 3D level gives rise to heerying emission spectra one has to excite the atoms to If we An angular in all fundo U kq Fy= k 9, 92 x Sinazt ka,& 02 R? Sinzi d2 $1 af 9 [ 2 9x109x9.66810 45.964166 (1.30) * Sinza 2 0.23N 0.23 b a= E= m - 153.3 m/s2 1.58103 in ty direction. O: (il LDA, - 188