Question
Solve the following kindly . Suppose we throw a needle on a large sheet of paper, on which horizontal lines are drawn, which are at
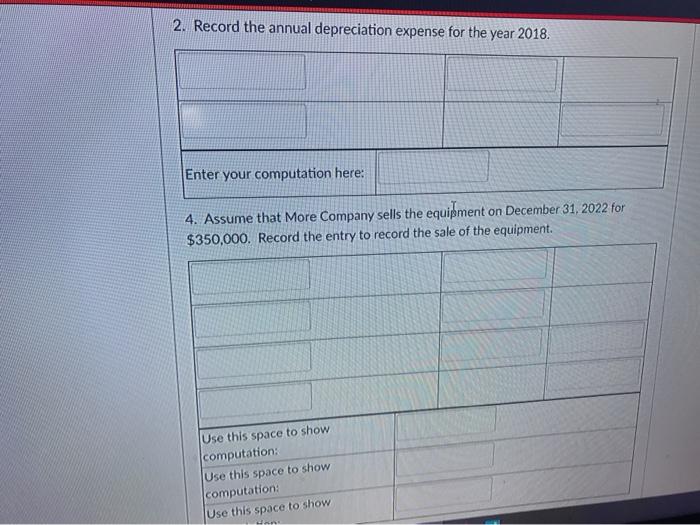

Solve the following kindly
.
Suppose we throw a needle on a large sheet of paper, on which horizontal
lines are drawn, which are at needle-length apart (see also Exercise 21.16).
Choose one of the horizontal lines as x-axis, and let (X, Y ) be the center of the
needle. Furthermore, let Z be the distance of this center (X, Y ) to the nearest
horizontal line under (X, Y ), and let H be the angle between the needle and
the positive x-axis.
a. Assuming that the length of the needle is equal to 1, argue that Z has
a U(0, 1) distribution. Also argue that H has a U(0, ?) distribution and
that Z and H are independent.
b. Show that the needle hits a horizontal line when
Z ?
1
2 sin H or 1 ? Z ?
1
2 sin H.
c. Show that the probability that the needle will hit one of the horizontal
lines equals 2
(a) For the Bayesian model given by ( | )~ ( , ) Y Bin n ? ? and the prior
? ?? ~ (,) Beta , find the posterior predictive density of a future data
value x, whose distribution is defined by ( | , )~ ( , ) x y Bin m ? ? .
(b) A bent coin is tossed 20 times and 6 heads come up. Assuming a flat
prior on the probability of heads on a single toss, what is the probability
that exactly one head will come up on the next two tosses of the same
coin? Answer this using results in (a).Chapter 3: Bayesian Basics Part 3
123
(c) A bent coin is tossed 20 times and 6 heads come up. Assume a
Beta(20.3,20.3) prior on the probability of heads.
Find the expected number of times you will have to toss the same coin
again repeatedly until the next head comes up.
(d) A bent coin is tossed 20 times and 6 heads come up. Assume a
Beta(20.3,20.3) prior on the probability of heads.
Now consider tossing the coin repeatedly until the next head, writing
down the number of tosses, and then doing all of this again repeatedly,
again and again.
The result will be a sequence of natural numbers (for example
3, 1, 1, 4, 2, 2, 1, 5, 1, ....), where each number represents a number of
tails in a row within the sequence, plus one.
Next define ? to be the average of a very long sequence like this (e.g.
one of length 1,000,000). Find the posterior predictive density and mean
of ? (approximately)
In how many ways 5 boys and 3 girls can be seated in a row, so that no two girls are
together?
3. How many 6- digit telephone numbers can be constructed with the digits
0,1,2,3,4,5,6,7,8,9 if each numbers starts with 35 and no digit appear more than
once?
4. Find the number of arrangements that can be made out of the letters of the word
"ASSASSINATION"
5. (a) In how many ways can 8 identical beads be strung on a necklace?
(b) In how many ways can 8 boys form a ring?
6. Find the rank of the word 'CHAT' in dictionary.
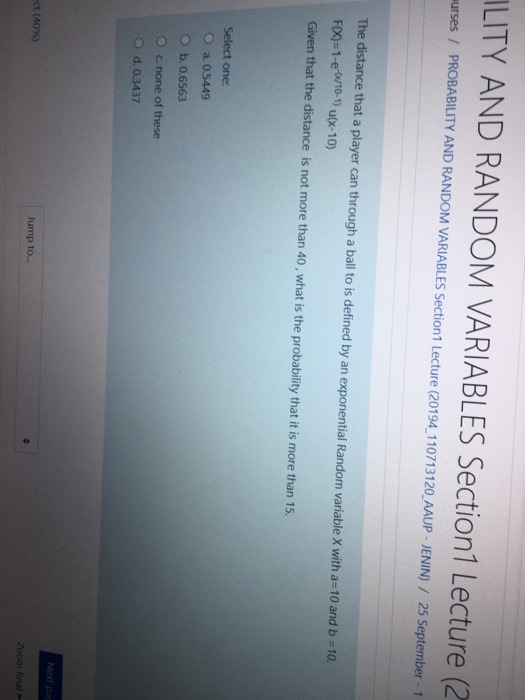
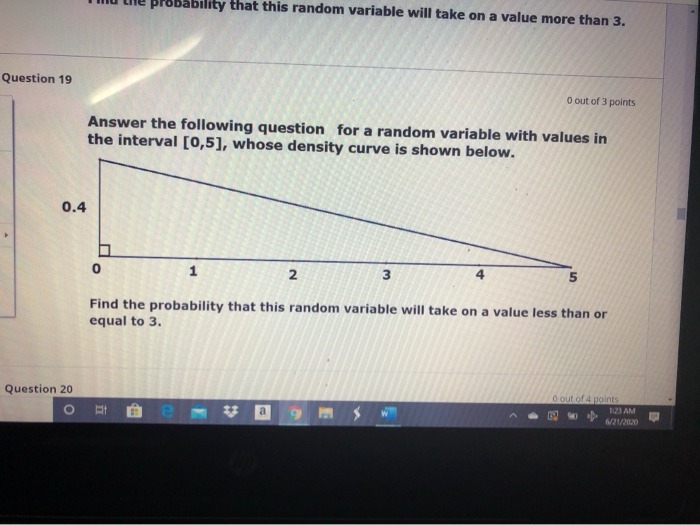
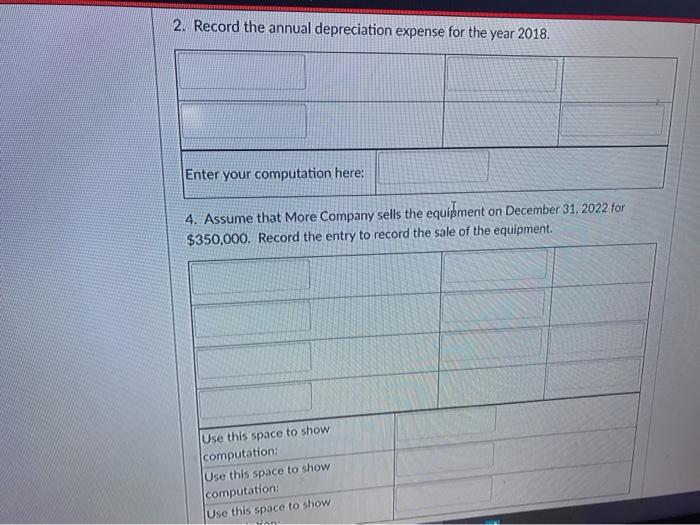

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


