@ solve the following please
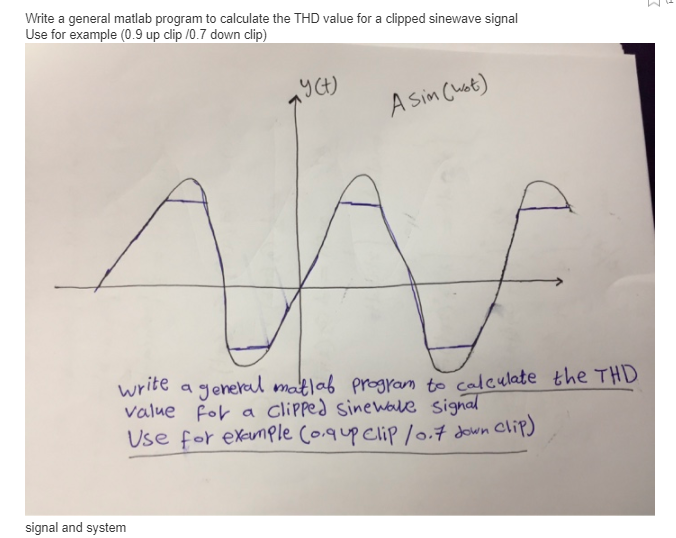
1. In the lab we analyzed filtering 60 Hz power-line noise from ECG signal using a digital (signal processing) filter. Now let's try to an analog (circuit) filter approach to remove the 60 Hz line-noise. Following is an active twin-T notch filter with transfer function: Z(@) (1+m)((2joRC) +1) R H(@) = X(@) (2joRC) +4(1-m)joRC+1 X Z 2R 2R Here m is the ratio of the two feedback resistance which determines the gain and quality 2C MR R for the filter. The drop frequency of this twin-T notch filter is fdrop=1/4ARC. For designing a 60 Hz drop filter, let's use R=10 kQ and C=133 nF. (a) Form={0.8, 0.9} plot the magnitude and phase response of H( W ) with a range of f=w/2n=[0, 200 Hz]. (b) Consider the ECG signal used during the class (ecg_signal . mat) as the input (x(t)=ecg) of a 60 Hz twin-T notch filter with m=0 . 9. Using the functions fft( ) and ifft ( ), determine the X (w), Z (@), and z ( t ) [z (t ) is the output signal from the twin-T notch filter]. Plot x ( t ), X( f ), Z( f ), and z ( t ) in a 4x1 subplot for the range of -250 f 250 and O Sts 2.5. [Please pay attention to the proper use of fitshift( ) and ifftshift ( ) while solving this problem.] 2. Calculate the energy of time domain signal x ( t ) and z ( t ) for the range of 0 St$2.5. Also calculate the energy of these signals in frequency domain using Parseval's theorem. Plot Energy (X) and Energy ( Z ) as a function of frequency f in a 2x1 subplot (Energy vs frequency plot is know as energy spectrum of a signal).Write a general matlab program to calculate the THD value for a clipped sinewave signal Use for example (0.9 up clip /0.7 down clip) A Sim (wot) write a general matlab program to calculate the THD value for a clipped sinewave signal Use for example (o.9 up clip /0.7 down clip) signal and systemPlease help write a MATLAB script for #3. 1. A time domain real-signal x ( t ) has a Fourier Transform property of x (w ) = X* (-W). Consider the following frequency domain description of a signal G ( W) : G(W)= 2, 5 5 w S10 0, elsewhere (a) Evaluate g (t ) using the definition of Inverse Fourier Transformation 8(1)= JG(we do Plot G(w), Re(g(t) ), and Im(g(t) ) in a 3x1 subplot for the interval W=-31. 4:0. 01:31 . 4 and t=-100:0. 1: 100. (b) Now consider Y ( W) =G(@-5 ) . Plot Y (w), Re (y (t) ), and Im(y (t) ) in a 3x1 subplot with the same intervals. (c) Are g ( t ) and y ( t ) real-signal or complex signal? 2. When the signal g ( t ) goes through a filter h ( t ) where the frequency domain definition of the filter is: H(@) = 5 0 , w S 20 0, elsewhere the results in a time domain output signal: m(t). (a) Using convolution theorem, calculate the frequency domain output signal M (w). Plot the magnitude and phase of M(w ) in a 2x1 subplot for the interval W=-31 . 4:0. 01:31.4. (b) Evaluate m( t ) using the definition of Inverse Fourier Transformation. Plot Re(m( t) ) and Im(m( t ) ) in a 2x1 subplot for the interval t=-100:0. 1 : 100.3. Calculate the energy of the output signal m( t ) for the time range t=-100:0. 1: 100. Also evaluate the energy of the output signal in frequency domain using Parseval's theorem (use the frequency range W=31 . 4:0. 01:31.4).1. (10 pts) Consider the circuit depicted in the LC following figure. If v, (t) = 50 cos(1000t) V determine the instantaneous power p(c) dissipated 6 mF by the 100 Q resistor in the following circuit. Find the power being dissipated by the resistor at t = 2 ms. 1000 15 ml = p(t) = (8 pts) P(2 ms) = (2 pts) 2. (10 pts) A voltage source, v, = 100u(t) V, a & = 6 ml inductor, and a R = 15 Q resistor form a series circuit. Find the power being absorbed by the inductor and by the resistor at t = 1 ms, and determine the power being delivered by the voltage source att = 1 ms. mm PR(1 ms) = (3 pts) 6 mH PL (1 ms) = (3 pts) 15 0 Ps(1 ms) = (4 pts) 3. (10 pts) A current source of is = 5 cos 100t A, a 5 Q resistor, 15 Q resistor and a 5 mF capacitor are in parallel. Assume steady-state conditions exist. Find the instantaneous power being absorbed or 50 15 0 5 mF delivered by the (a) 5 Q resistor; (b) 15 Q resistor; (c) 5 mF capacitor; (d) sinusoidal source. (a) PER(t) = (2 pts) (b) Pisa (t) = (2 pts) (c) pc(t) = (3 pts) (d) ps(t) = (3 pts) 4. (10 pts) Given the phasor voltage V = 100 2120* V across an impedance Z = 20245 0, obtain an expression for the instantaneous power, and compute the average power if w = 120n rad/s. P() = (5 pts) Paverage= (5 pts)Answer! The Following Questions 1. Use MATLAB to calculate the following quantities: (a) 5H (b) 55+37 (c) 91.25 2. If the volume of a cylinder of height h and radius r is given by V = rrh, use MATLAB to find the volume enclosed by a cylinder that is 12 cm high with a diameter of 4 cm. 3. Use MATLAB to compute the sin of x/3 expressed as a rational number. 4. Create a MATLAB m file to display the results of sin (7/4), sin (#/3), sin (x/2) as rational numbers. 5. Write a MATLAB routine to ask the user for the radius and height of a cylinder and return the volume. 6. Use MATLAB to enter 7v2-5v60 +5:8 as a string, then find the numerical value. 7. Compute 3:01, both as an approximate floating point number and as an exact integer (written in usual decimal notation). 8. Compute: (a) 1111 -345. (b) eld and 382801# to 15 digits each. Which is bigger? (c) the fractions 2709/1024, 10583/4000, and 2024/765. Which of these is the best approximation to v77 9. Compute to 15 digits: (a) cosh (0,1). (b) In(2). (Hint: The natural logarithm in MATLAB is called log, not In.) (c) arctan (1/2). (Hint: The inverse tangent function in MATLAB is called atan, not arctan.) 10. Define the variable x as x = 2.34, then evaluate: (a) 2x - 6x + 14.8x2 +9.1 (b) V14+x X
