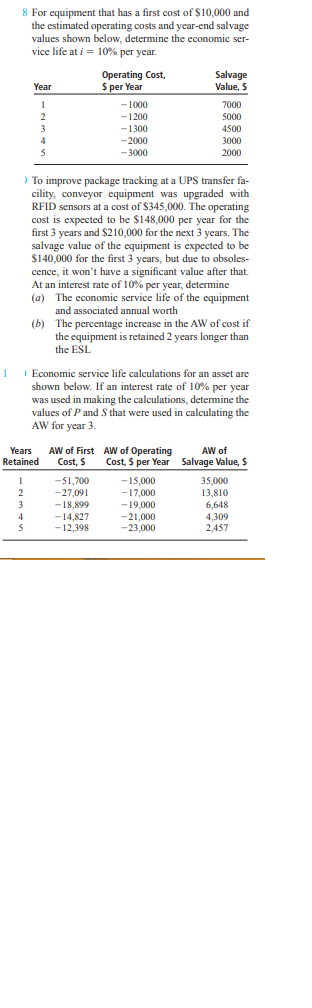
solve the following

Tom, the owner of Burger Palace, determined that his weighted average cost of capital is 8%. He ex- pects a return of 4% per year on all of his invest- ments. A proposal presented by the owner of the Dairy Choice next door seems quite risky to Tom, but is an intriguing partnership opportunity. Tom has determined that the proposal's "risk factor" will require an additional 3% per year return for him to accept it. (a) Use the recommended approach to determine the MARR that Tom should use, and explain how the 3% risk factor is compensated for in this MARK. (b) Determine the effective MARR for his busi- ness if Tom turns down the proposal. Mix and WACC Electrical generators produce not only electricity, but also heat from conductor resistance and from friction losses in bearings. A company that manu- factures generator coolers for nuclear and gas tur- bine power plants undertook a plant expansion through financing that had a debt-equity mix of 45-55. If $18 million came from mortgages and bond sales, what was the total amount of the financing? Determine the debt-to-equity mix when Applied Technology bought out Southwest Semiconductor using financing as follows: $12 million from mort- gages, $5 million from retained earnings, $10 mil- lion from cash on hand, and $20 million from bonds.Why is it financially unhealthy for an individual to maintain a large percentage of debt financing over a long time, that is, to be highly leveraged? In a leveraged buyout of one company by another, the purchasing company usually obtains borrowed money and inserts as little of its own equity as pos- sible into the purchase. Explain some circum- stances under which such a buyout may put the purchasing company at economic risk. Grainger and Company has an opportunity to in- vest $500,000 in a new line of direct-drive rotary screw compressors. Financing will be equally split between common stock ($250,000) and a loan with an 8% after-tax interest rate. The estimated annual NCF after taxes is $48,000 for the next 7 years. The effective tax rate is 50%. Grainger uses the capital asset pricing model for evaluation of its common stock. Recent analysis shows that it has a volatility rating of 0.95 and is paying a pre- mium of 5% above a safe return on its common stock. Nationally, the safest investment is cur- rently paying 3% per year. Is the investment finan- cially attractive if Grainger uses as the MARR its (a) equity cost of capital and (b) WACC?8 For equipment that has a first cost of $10,000 and the estimated operating costs and year-end salvage values shown below, determine the economic ser- vice life at i = 10% per year. Operating Cost, Salvage Year $ per Year Value, $ -1000 7000 - 1200 5000 -1300 4500 -2000 3000 -3000 2000 ) To improve package tracking at a UPS transfer fa- cility, conveyor equipment was upgraded with RFID sensors at a cost of $345,000. The operating cost is expected to be $148,000 per year for the first 3 years and $210,000 for the next 3 years. The salvage value of the equipment is expected to be $140,000 for the first 3 years, but due to obsoles- cence, it won't have a significant value after that. At an interest rate of 10% per year, determine (a) The economic service life of the equipment and associated annual worth The percentage increase in the AW of cost if the equipment is retained 2 years longer than the ESL | Economic service life calculations for an asset are shown below. If an interest rate of 10% per year was used in making the calculations, determine the values of P and S that were used in calculating the AW for year 3. Years AW of First AW of Operating AW of Retained Cost, $ Cost, $ per Year Salvage Value, $ -51,700 -15,000 35,000 -27,091 -17,000 13,810 - 18,899 -19,000 6,648 -14,827 -21,000 4,309 -12,398 -23,000 2,457Chebyshev's inequality, (see Exercise 44, Chapter 3), is valid for continuous as well as discrete distributions. It states that for any number k satisfying k 2 1, P(IX - p 2ko) =1/k (see Exercise 44 in Chapter 3 for an interpretation). Obtain this probability in the case of a normal distribution for , 2, and 3, and compare to the upper bound. Reference exercise 44 A result called Chebyshev's inequality states that for any probability distribution of an rv X and any number k that is at least 1, P( | X - p | k o) $ 1/k2 . In words, the probability that the value of X lies at least k standard deviations from its mean is at most 1/12. a. What is the value of the upper bound for k = 2? K + 3? K = 4? K= 5? K = 10? b. Compute p and o for the distribution of Exercise 13. Then evaluate P()X - p| 2 ko) for the values of k given in part (a). What does this suggest about the upper bound relative to the corresponding probability? c. Let X have possible values -1, 0, and 1, with probabilities 1/18, 8/9 and 1/8 , respectively. What is P(1X - p/2 30), and how does it compare to the corresponding bound? d. Give a distribution for which P(IX - p|2 50) = .04.Sales delay is the elapsed time between the manufacture of a product and its sale. According to the article "Warranty Claims Data Analysis Considering Sales Delay" (Quality and Reliability Engr. Intl., 2013: 113-123), it is quite common for investigators to model sales delay using a lognormal distribution. For a particular product, the cited article proposes this distribution with parameter values p= 2.05 and of = .06 (here the unit for delay is months). a. What are the variance and standard deviation of delay time? b. What is the probability that delay time exceeds 12 months? c. What is the probability that delay time is within one standard deviation of its mean value? d. What is the median of the delay time distribution? e. What is the 99th percentile of the delay time distribution? f. Among 10 randomly selected such items, how many would you expect to have a delay time exceeding 8 months?A certain market has both an express checkout line and a superexpress checkout line. Let X1 denote the number of customers in line at the express checkout at a particular time of day, and let X2 denote the number of customers in line at the superexpress checkout at the same time. Suppose the joint pmf of X1 and X2 is as given in the accompanying table. XI a. What is P(X, = 1, X2 = 1), that is, the probability that there is exactly one customer in each line? b. What is P(X, = X2), that is, the probability that the numbers of customers in the two lines are identical? c. Let A denote the event that there are at least two more customers in one line than in the other line. Express A in terms of X, and X2, and calculate the probability of this event. d. What is the probability that the total number of customers in the two lines is exactly four? At least four