Solve using Excel Solver and set the Solving Method to Simplex LP

Scheduling umpires is a classic application of Integer Programming. Were going to simulate on a much smaller level using the 14 teams of the Sally League (old nickname for the Southern Atlantic League or SAL). Consider the planned schedule for the last two June series of the 2021 season.

The games on 6/25 through 6/27 represent a (typical) 3 game series, as do the games from 6/28 through 6/30.

Games played on 6/27 (Umpire crew designation also shown).

CREW 1 Hagerstown at Delmarva CREW 2 Lakewood at Greensboro CREW 3 West Virginia at Kannapolis CREW 4 Lexington at Asheville CREW 5 - Augusta at Greenville CREW 6 - Hickory at Charleston CREW 7 - Rome at Columbia

Note the abbreviations used.

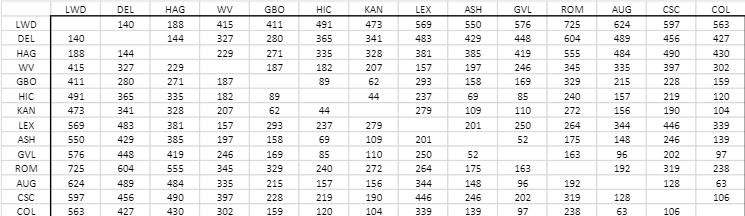
LWD Lakewood; DEL Delmarva; HAG Hagerstown; WV West Virginia; GBO Greensboro; HIC Hickory; KAN Kannapolis; LEX Lexington; ASH Asheville; GVL Greenville; ROM Rome; AUG Augusta; CSC Charleston; COL Columbia

Games played on 6/28 (through 6/30)

Hagerstown @ Lakewood; Greensboro @ Delmarva; West Virginia @Hickory; Augusta @ Lexington; Greenville @ Rome; Asheville @ Charleston; Kannapolis @ Columbia

One could develop a sophisticated, generic model that could be used for scheduling umpire travel at any point in the schedule. For this example though, were just interested in a simple model that will determine how the umpire crews should travel from June 27th to June 28th (between the two series). Your task: DETERMINE WHICH CREWS ARE ASSIGNED TO specific games in the June 28th BASEBALL SERIES!The objective is to minimize combined miles traveled by the crews (the members of the crews stay together). Unless you really want to as a personal challenge, dont make the model harder or more elaborate than necessary. This is a good modeler/model partnership situation. Besides minimizing overall distance traveled, and the fact that each of the 7 crews must be assigned to exactly 1 series (and each series assigned a crew!), there are some scenarios with additional requirements we want to compare and contrast the resulting umpire travel schedule.

Solve each model separately.

Model 1) A crew cannot umpire at the same location in the 6/28 series as they did in the 6/25 series. (So, e.g., Crew 1 cannot umpire at Delmarva in the second series).

Model 2) - In addition to requirement in 1), add the requirement that a crew can only be assigned to a series for teams they did NOT serve as a crew for in 6/25 Series. So, for example, CREW 1 cannot be assigned to 6/28 series that has Delmarva or Hagerstown participating.

Model 3) - To increase crew travel equity, add on to the requirements for Model 1 and Model2, that no crew can travel less than 150 miles. (Modeling hint: Do this in the same manner as you did the other restrictions).

In each of the three scenarios, summarize how the crews travel. Compare and contrast the crew schedules and note the difference in the total mileage. Shown below (and provided in Canvas) is a large 14x14 distance matrix for the entire league. You do not need all this data use only the distance data you need to implement your model that determines which crew is assigned to which 6/28 game/series

w ASH AUG 4 12 LWD 1 GBO @GBO @GBO HAG HAG HAG 25-Jun|Thu 26-Jun Fri 27-Jun Sat 28-Jun Sun 29-Jun Mon 30-Jun Tue DEL 2 HAG HAG HAG GBO GBO GBO HAG 3 DEL DEL DEL LWD LWD @LWD GBO 5 LWD LWD LWD DEL DEL @DEL KAN KAN KAN @HIC @HIC HIC HIC 6 esc ecsc @CSC WV KAN 7 WV wy wy ecol ecol eCOL LEX 8 DASH @ASH ASH AUG AUG AUG ROM 11 COL COL COL GVL 10 AUG AUG AUG @ROM @ROM @ROM LEX LEX LEX esc esc @CSC GVL GVL GVL LEX LEX LEX CSC 13 HIC HIC HIC ASH ASH ASH COL 14 ROM ROM ROM KAN GVL wy KAN GVL GVL w KAN DEL 140 HAG 188 144 wv 415 GBO 411 280 271 187 HIC 491 365 335 182 89 144 327 GVL 576 448 419 246 169 85 110 250 52 280 365 341 229 271 335 328 381 385 419 555 484 490 430 483 429 448 604 489 456 427 187 182 207 157 197 246 345 COL 563 427 430 302 159 120 104 339 139 97 238 63 106 89 62 293 158 169 329 215 228 44 237 69 85 240 157 219 120 mmm m do 163 96 202 97 D DN NW 00 5 6 1 5 3 9 m w ASH AUG 4 12 LWD 1 GBO @GBO @GBO HAG HAG HAG 25-Jun|Thu 26-Jun Fri 27-Jun Sat 28-Jun Sun 29-Jun Mon 30-Jun Tue DEL 2 HAG HAG HAG GBO GBO GBO HAG 3 DEL DEL DEL LWD LWD @LWD GBO 5 LWD LWD LWD DEL DEL @DEL KAN KAN KAN @HIC @HIC HIC HIC 6 esc ecsc @CSC WV KAN 7 WV wy wy ecol ecol eCOL LEX 8 DASH @ASH ASH AUG AUG AUG ROM 11 COL COL COL GVL 10 AUG AUG AUG @ROM @ROM @ROM LEX LEX LEX esc esc @CSC GVL GVL GVL LEX LEX LEX CSC 13 HIC HIC HIC ASH ASH ASH COL 14 ROM ROM ROM KAN GVL wy KAN GVL GVL w KAN DEL 140 HAG 188 144 wv 415 GBO 411 280 271 187 HIC 491 365 335 182 89 144 327 GVL 576 448 419 246 169 85 110 250 52 280 365 341 229 271 335 328 381 385 419 555 484 490 430 483 429 448 604 489 456 427 187 182 207 157 197 246 345 COL 563 427 430 302 159 120 104 339 139 97 238 63 106 89 62 293 158 169 329 215 228 44 237 69 85 240 157 219 120 mmm m do 163 96 202 97 D DN NW 00 5 6 1 5 3 9 m