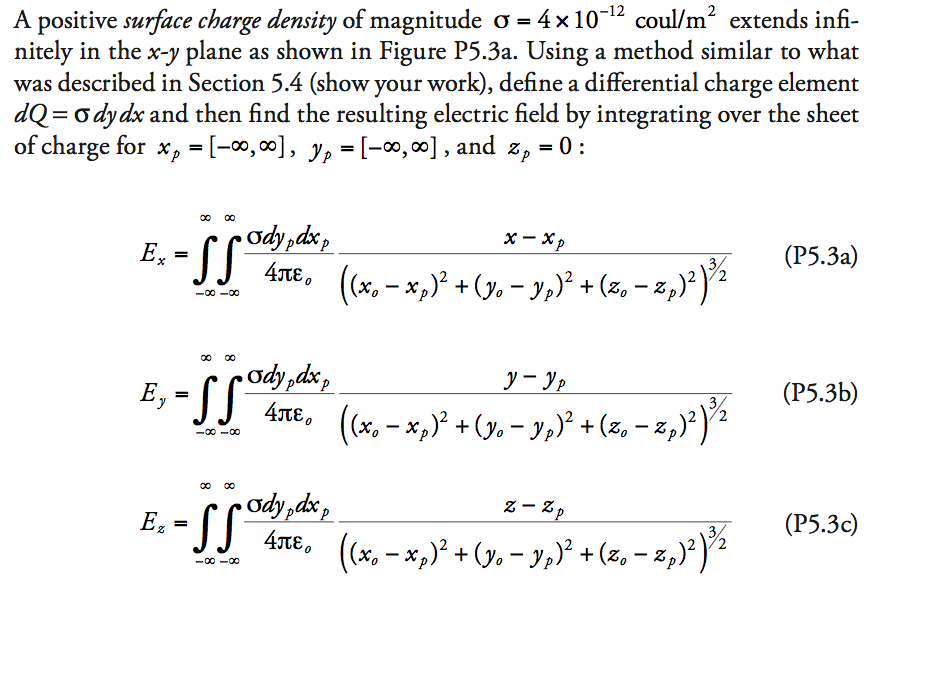
some example is provided which is likely similar to this problem:
A positive surjace charge density of magnitude -4x10-12 coul/m2 extends infi- nitely in the x-y plane as shown in Figure P5.3a. Using a method similar to what was described in Section 5.4 (show your work), define a differential charge element dQ= aax and then find the resulting electric field by integrating over the sheet of charge for X,- , y,--, oj, and z,-0: 00 Co x-x 2(P5.3a) 2 (P53b) 0 Z- Z 2 2(P5.3c) Measurement point dE Sheet charge with surface charge density coul/m Differential charge element dcdy 0 p/ Sheet charge with surface charge density coul/m2 located at z 1 mm Sheet charge with surface charge density -o coul/m2 located atz-1 mm Figure P5.3 (a) The differential electric field dE at observation point f, due to a differential sheet charge element ddy located on the x-y plane. (b) Two parallel and oppositely charged sheet charges located on the planes zp-+1mm and zp--1mm 1. Write a MATLAB program using the dblquad function to calculate E, E and E, at the following points x,,y,, zo [0, 0, 2 10-3] (above the plate) x,,y,, z.-[ 30 x 10-3,-5 x 10-3, 12 x 10-3 ] (below the plate) Assume that 10 is a good enough approximation for infinity. Note that by symmetry, the x andy components of the field should integrate to zero (or close to it). Confirm this result 2. Now, assume that there are two sheet charges in the planes parallel to the x-y plane: the first sheet located at zp -+1 mm with surface charge density -4 10-12 coul/m 2 and the second sheet located at ze--1 mm and oppo- sitely charged with surface charge density 4 10-12 coul/m 2 (see Figure P5.3b). Find the electric field via superposition by calculating the electric field 150 Numerical and Analytical Methods with MATLAB separately for each sheet and then adding them together. Find E, E,, and E, or the these three points: above the plates) (between the plates) (below the plates) X o[0, 0, 2 x 10-3] xo,yo, z10 x 10-3, 0,-0.5 x 10-3 x,Joz.-[ 30x10-3,-5x 10-3, 12x10-3 ] Print out the results. Do these results make sense? Example 5 9.m % This program calculates the surface area and volume f % a hemisphere (with radius-1) using dblquad. The exact % values from formulae are also calculated. clear; clc; global R; R-li % calculate surface area SAdblquad ('hemisphere_ dA',0,pi/2,0,2*pi); SA exact 2*pi*R*2; calculate volume V- dblquad ( 'hemisphere_dv',-R,R, -R, R) V_exact2/3*pi R 3; % print results fprintf ('Surface area SA of a hemisphere of'); fprint f ('radius % .4 f min ' ,R) ; fprintf ('SA by DBLQUAD- %. 4 f m^2 ', sA) ; fprintf(' SA exact print f ('Volume V of a hemisphere of radius % .4 f m ', R) ; %, 4 f m^2 ', SA exact) ; = Numerical and Analytical Methods with MATLAB fprintf('V exact % hemisphere-da.m: This function defines the integrand % for determining the surface area of a hemisphere and is % used in MATLAB's dbIquad function function [ dA -hemisphere_dA( phi, theta) global R; dA R 2 * sin(phi); A positive surjace charge density of magnitude -4x10-12 coul/m2 extends infi- nitely in the x-y plane as shown in Figure P5.3a. Using a method similar to what was described in Section 5.4 (show your work), define a differential charge element dQ= aax and then find the resulting electric field by integrating over the sheet of charge for X,- , y,--, oj, and z,-0: 00 Co x-x 2(P5.3a) 2 (P53b) 0 Z- Z 2 2(P5.3c) Measurement point dE Sheet charge with surface charge density coul/m Differential charge element dcdy 0 p/ Sheet charge with surface charge density coul/m2 located at z 1 mm Sheet charge with surface charge density -o coul/m2 located atz-1 mm Figure P5.3 (a) The differential electric field dE at observation point f, due to a differential sheet charge element ddy located on the x-y plane. (b) Two parallel and oppositely charged sheet charges located on the planes zp-+1mm and zp--1mm 1. Write a MATLAB program using the dblquad function to calculate E, E and E, at the following points x,,y,, zo [0, 0, 2 10-3] (above the plate) x,,y,, z.-[ 30 x 10-3,-5 x 10-3, 12 x 10-3 ] (below the plate) Assume that 10 is a good enough approximation for infinity. Note that by symmetry, the x andy components of the field should integrate to zero (or close to it). Confirm this result 2. Now, assume that there are two sheet charges in the planes parallel to the x-y plane: the first sheet located at zp -+1 mm with surface charge density -4 10-12 coul/m 2 and the second sheet located at ze--1 mm and oppo- sitely charged with surface charge density 4 10-12 coul/m 2 (see Figure P5.3b). Find the electric field via superposition by calculating the electric field 150 Numerical and Analytical Methods with MATLAB separately for each sheet and then adding them together. Find E, E,, and E, or the these three points: above the plates) (between the plates) (below the plates) X o[0, 0, 2 x 10-3] xo,yo, z10 x 10-3, 0,-0.5 x 10-3 x,Joz.-[ 30x10-3,-5x 10-3, 12x10-3 ] Print out the results. Do these results make sense? Example 5 9.m % This program calculates the surface area and volume f % a hemisphere (with radius-1) using dblquad. The exact % values from formulae are also calculated. clear; clc; global R; R-li % calculate surface area SAdblquad ('hemisphere_ dA',0,pi/2,0,2*pi); SA exact 2*pi*R*2; calculate volume V- dblquad ( 'hemisphere_dv',-R,R, -R, R) V_exact2/3*pi R 3; % print results fprintf ('Surface area SA of a hemisphere of'); fprint f ('radius % .4 f min ' ,R) ; fprintf ('SA by DBLQUAD- %. 4 f m^2 ', sA) ; fprintf(' SA exact print f ('Volume V of a hemisphere of radius % .4 f m ', R) ; %, 4 f m^2 ', SA exact) ; = Numerical and Analytical Methods with MATLAB fprintf('V exact % hemisphere-da.m: This function defines the integrand % for determining the surface area of a hemisphere and is % used in MATLAB's dbIquad function function [ dA -hemisphere_dA( phi, theta) global R; dA R 2 * sin(phi)
