sorry this is a lot but plz format as C++

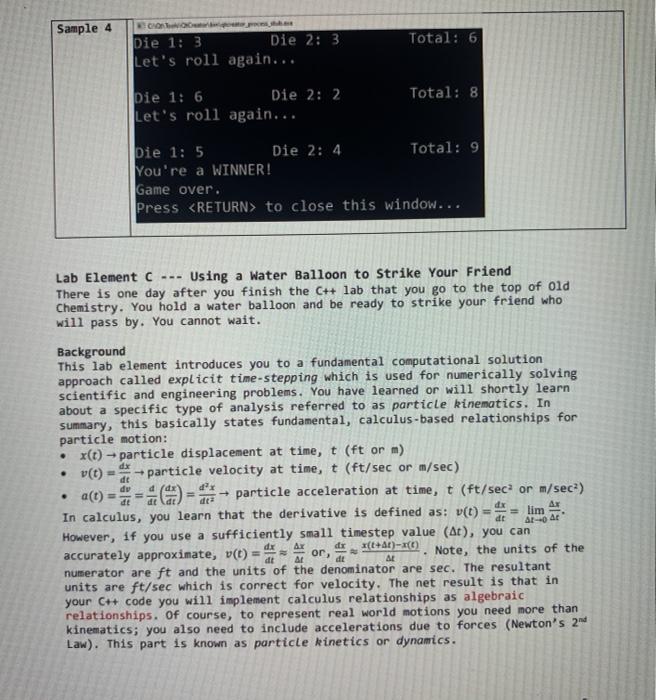
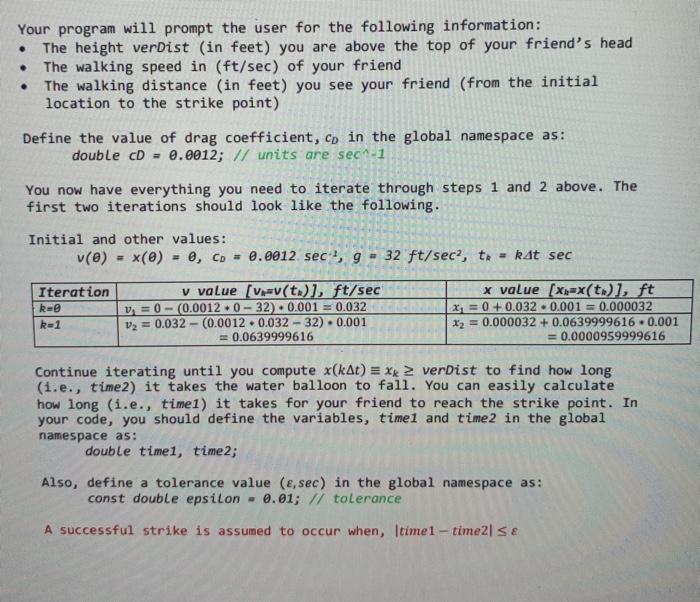
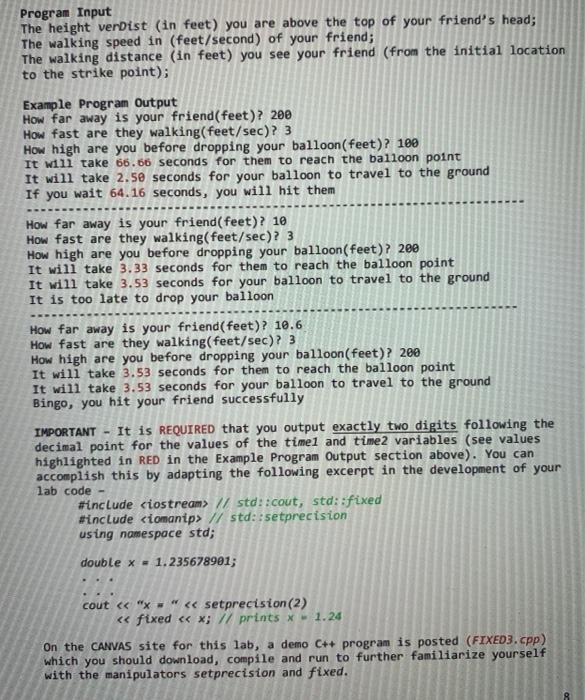
Sample 4 BONO Die 1: 3 Die 2: 3 Let's roll again... Total: 6 Total: 8 pie 1: 6 Die 2: 2 Let's roll again... pie 1: 5 Die 2: 4 Total: 9 You're a WINNER! Game over. Press to close this window... Lab Element C --- Using a Water Balloon to Strike Your Friend There is one day after you finish the C++ lab that you go to the top of old Chemistry. You hold a water balloon and be ready to strike your friend who will pass by. You cannot wait. dx Background This lab element introduces you to a fundamental computational solution approach called explicit time-stepping which is used for numerically solving scientific and engineering problems. You have learned or will shortly learn about a specific type of analysis referred to as particle kinematics. In summary, this basically states fundamental, calculus-based relationships for particle motion: x(t)- particle displacement at time, t (ft or m) - particle velocity at time, t (ft/sec or m/sec) dy d a(t) particle acceleration at time, t (ft/sec? or m/sec) In calculus, you learn that the derivative is defined as: v(t) == lim Ar However, if you use a sufficiently small timestep value (At), you can dr x(+1)-() accurately approximate, v(t) = or, Note, the units of the numerator are ft and the units of the denominator are sec. The resultant units are ft/sec which is correct for velocity. The net result is that in your C++ code you will implement calculus relationships as algebraic relationships. Of course, to represent real world motions you need more than kinematics; you also need to include accelerations due to forces (Newton's 2nd Law). This part is known as particle kinetics or dynamics. dt dt AL Specification To compute the position of your water balloon you need to account for both balloon kinematics and kinetics in your code. The forces that you need to account for are: gravitational force and aerodynamic drag. In your code, you need to include the accelerations associated with these forces. The acceleration due to gravity is easy. It is a constant, g = 32 ft/sec?. The effect of aerodynamic dragon balloon acceleration is a little trickier. It will be implemented using a simplified model, Qdrag = cpv (ft/sec?), where, co- 0.0012 sec-1 - constant drag coefficient. With these implementations, the model for balloon motion is given by, dv d2x dt dez-Cov(t) + g. ft/sec? a= . It is applied subject to the following definitions and constraints: In this expression, balloon displacement, *(t) and velocity, v) are taken as positive downwards and negative upwards. Since you are dropping the balloon from the top of Old Chem (x = 0), your calculations for balloon displacement and velocity should be > O for t > 0 Acceleration due to gravity is always downward; aerodynamic drag acts opposite to v It is assumed that you simply let go of the balloon from the top of old Chem. As a result, the initial balloon velocity is v(t = 0) = 0 The solution process uses a multistage, time-stepping algorithm. You will solve the balloon equation at discrete time intervals, ts, 12.03... Iki..., r where x = kat, sec in multiple steps starting at t= 0 (k = 0): Step 1 Step 2 Solve for Vx+1 = v*- (coux-9)at, for k = 0,1,2,... x(0= 0, v0 =0 Solve for Xk+1 = Xx + 2x+14t, for k=0,1,2,.-- k + k +1 Repeat Step 1 Set the time step interval to, At = 0.001 sec - constant Assume that you know how high you are above the top of your friend's head, and you know the walking speed and the walking distance of your friend. Based on the walking distance and walking speed of your friend, you can predict how many seconds (or minutes) your friend will take to reach the strike point. This time interval is referred to as timel. Next, the most important thing is to predict how long it will take for the balloon to fall on the head of your friend. Refer to this time interval as time2. For this simulation neglect your friend's physical height. . . Your program will prompt the user for the following information: The height verDist (in feet) you are above the top of your friend's head The walking speed in (ft/sec) of your friend The walking distance (in feet) you see your friend (from the initial location to the strike point) Define the value of drag coefficient, cp in the global namespace as: double cD = 0.0012; // units are sec1-1 You now have everything you need to iterate through steps 1 and 2 above. The first two iterations should look like the following. Initial and other values: v(e) x(O) = 0, Cp = 0.0012 sec9 = 32 ft/sec, te = kat sec Iteration kue k=1 v value (v=v(t)], ft/sec v = 0 - (0.0012.0-32) 0.001 = 0.032 V2 = 0.032-(0.0012.0.032-32). 0.001 = 0.0639999616 x value (x =X(t)], ft x = 0 + 0.032. 0.001 = 0.000032 X2 = 0.000032 +0.0639999616. 0.001 = 0.0000959999616 Continue iterating until you compute x(kat) = xx verbist to find how long (i.e., time) it takes the water balloon to fall. You can easily calculate how long (i.e., timel) it takes for your friend to reach the strike point. In your code, you should define the variables, timel and time in the global namespace as: double time, time2; Also, define a tolerance value (e, sec) in the global namespace as: const double epsilon - 0.01; // tolerance A successful strike is assumed to occur when, Itimel-time2 se Program Input The height verbist (in feet) you are above the top of your friend's head; The walking speed in (feet/second) of your friend; The walking distance (in feet) you see your friend (from the initial location to the strike point); Example Program Output How far away is your friend(feet)? 200 How fast are they walking(feet/sec)? 3 How high are you before dropping your balloon(feet)? 100 It will take 66.66 seconds for them to reach the balloon point It will take 2.50 seconds for your balloon to travel to the ground If you wait 64.16 seconds, you will hit them How far away is your friend(feet)? 10 How fast are they walking(feet/sec)? 3 How high are you before dropping your balloon(feet)? 200 It will take 3.33 seconds for them to reach the balloon point It will take 3.53 seconds for your balloon to travel to the ground It is too late to drop your balloon hat your friend How far away is your friend(feet)? 10.6 How fast are they walking (feet/sec)? 3 How high are you before dropping your balloon(feet)? 200 It will take 3.53 seconds for them to reach the balloon point It will take 3.53 seconds for your balloon to travel to the ground Bingo, you hit your friend successfully IMPORTANT It is REQUIRED that you output exactly two digits following the decimal point for the values of the time1 and time2 variables (see values highlighted in RED in the Example Program Output section above). You can accomplish this by adapting the following excerpt in the development of your lab code #include // std::cout, std::fixed #include // std::setprecision using namespace std; double x - 1.235678901; cout to close this window... Lab Element C --- Using a Water Balloon to Strike Your Friend There is one day after you finish the C++ lab that you go to the top of old Chemistry. You hold a water balloon and be ready to strike your friend who will pass by. You cannot wait. dx Background This lab element introduces you to a fundamental computational solution approach called explicit time-stepping which is used for numerically solving scientific and engineering problems. You have learned or will shortly learn about a specific type of analysis referred to as particle kinematics. In summary, this basically states fundamental, calculus-based relationships for particle motion: x(t)- particle displacement at time, t (ft or m) - particle velocity at time, t (ft/sec or m/sec) dy d a(t) particle acceleration at time, t (ft/sec? or m/sec) In calculus, you learn that the derivative is defined as: v(t) == lim Ar However, if you use a sufficiently small timestep value (At), you can dr x(+1)-() accurately approximate, v(t) = or, Note, the units of the numerator are ft and the units of the denominator are sec. The resultant units are ft/sec which is correct for velocity. The net result is that in your C++ code you will implement calculus relationships as algebraic relationships. Of course, to represent real world motions you need more than kinematics; you also need to include accelerations due to forces (Newton's 2nd Law). This part is known as particle kinetics or dynamics. dt dt AL Specification To compute the position of your water balloon you need to account for both balloon kinematics and kinetics in your code. The forces that you need to account for are: gravitational force and aerodynamic drag. In your code, you need to include the accelerations associated with these forces. The acceleration due to gravity is easy. It is a constant, g = 32 ft/sec?. The effect of aerodynamic dragon balloon acceleration is a little trickier. It will be implemented using a simplified model, Qdrag = cpv (ft/sec?), where, co- 0.0012 sec-1 - constant drag coefficient. With these implementations, the model for balloon motion is given by, dv d2x dt dez-Cov(t) + g. ft/sec? a= . It is applied subject to the following definitions and constraints: In this expression, balloon displacement, *(t) and velocity, v) are taken as positive downwards and negative upwards. Since you are dropping the balloon from the top of Old Chem (x = 0), your calculations for balloon displacement and velocity should be > O for t > 0 Acceleration due to gravity is always downward; aerodynamic drag acts opposite to v It is assumed that you simply let go of the balloon from the top of old Chem. As a result, the initial balloon velocity is v(t = 0) = 0 The solution process uses a multistage, time-stepping algorithm. You will solve the balloon equation at discrete time intervals, ts, 12.03... Iki..., r where x = kat, sec in multiple steps starting at t= 0 (k = 0): Step 1 Step 2 Solve for Vx+1 = v*- (coux-9)at, for k = 0,1,2,... x(0= 0, v0 =0 Solve for Xk+1 = Xx + 2x+14t, for k=0,1,2,.-- k + k +1 Repeat Step 1 Set the time step interval to, At = 0.001 sec - constant Assume that you know how high you are above the top of your friend's head, and you know the walking speed and the walking distance of your friend. Based on the walking distance and walking speed of your friend, you can predict how many seconds (or minutes) your friend will take to reach the strike point. This time interval is referred to as timel. Next, the most important thing is to predict how long it will take for the balloon to fall on the head of your friend. Refer to this time interval as time2. For this simulation neglect your friend's physical height. . . Your program will prompt the user for the following information: The height verDist (in feet) you are above the top of your friend's head The walking speed in (ft/sec) of your friend The walking distance (in feet) you see your friend (from the initial location to the strike point) Define the value of drag coefficient, cp in the global namespace as: double cD = 0.0012; // units are sec1-1 You now have everything you need to iterate through steps 1 and 2 above. The first two iterations should look like the following. Initial and other values: v(e) x(O) = 0, Cp = 0.0012 sec9 = 32 ft/sec, te = kat sec Iteration kue k=1 v value (v=v(t)], ft/sec v = 0 - (0.0012.0-32) 0.001 = 0.032 V2 = 0.032-(0.0012.0.032-32). 0.001 = 0.0639999616 x value (x =X(t)], ft x = 0 + 0.032. 0.001 = 0.000032 X2 = 0.000032 +0.0639999616. 0.001 = 0.0000959999616 Continue iterating until you compute x(kat) = xx verbist to find how long (i.e., time) it takes the water balloon to fall. You can easily calculate how long (i.e., timel) it takes for your friend to reach the strike point. In your code, you should define the variables, timel and time in the global namespace as: double time, time2; Also, define a tolerance value (e, sec) in the global namespace as: const double epsilon - 0.01; // tolerance A successful strike is assumed to occur when, Itimel-time2 se Program Input The height verbist (in feet) you are above the top of your friend's head; The walking speed in (feet/second) of your friend; The walking distance (in feet) you see your friend (from the initial location to the strike point); Example Program Output How far away is your friend(feet)? 200 How fast are they walking(feet/sec)? 3 How high are you before dropping your balloon(feet)? 100 It will take 66.66 seconds for them to reach the balloon point It will take 2.50 seconds for your balloon to travel to the ground If you wait 64.16 seconds, you will hit them How far away is your friend(feet)? 10 How fast are they walking(feet/sec)? 3 How high are you before dropping your balloon(feet)? 200 It will take 3.33 seconds for them to reach the balloon point It will take 3.53 seconds for your balloon to travel to the ground It is too late to drop your balloon hat your friend How far away is your friend(feet)? 10.6 How fast are they walking (feet/sec)? 3 How high are you before dropping your balloon(feet)? 200 It will take 3.53 seconds for them to reach the balloon point It will take 3.53 seconds for your balloon to travel to the ground Bingo, you hit your friend successfully IMPORTANT It is REQUIRED that you output exactly two digits following the decimal point for the values of the time1 and time2 variables (see values highlighted in RED in the Example Program Output section above). You can accomplish this by adapting the following excerpt in the development of your lab code #include // std::cout, std::fixed #include // std::setprecision using namespace std; double x - 1.235678901; cout