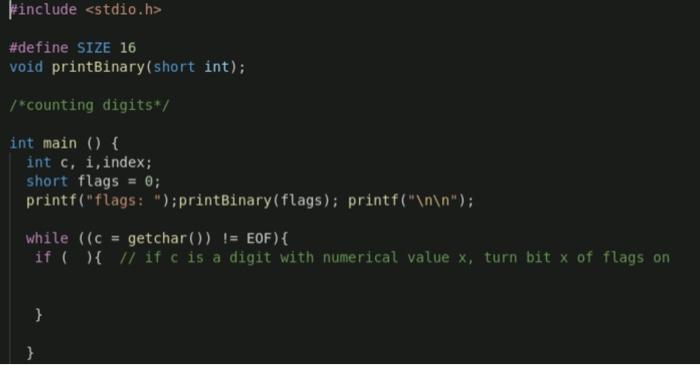
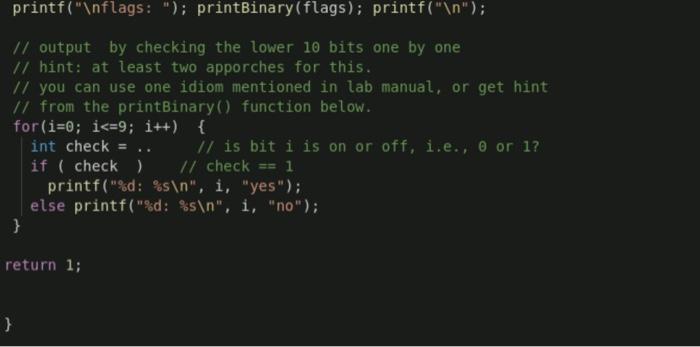
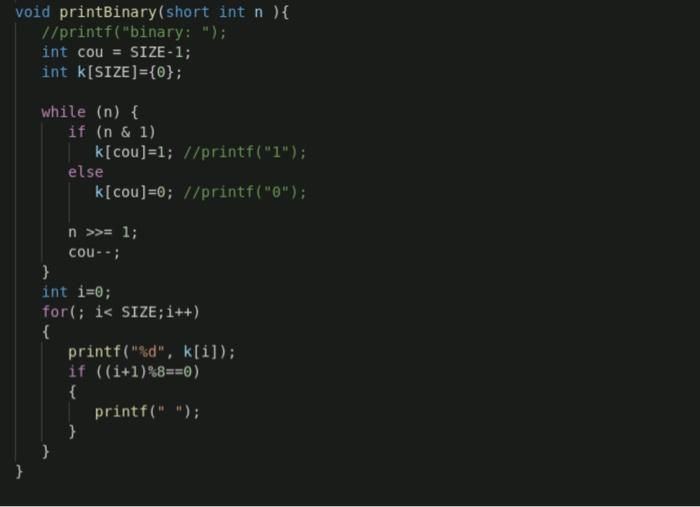
Specification In class we mentioned that one usefulness of bitwise operator is to use bits as Boolean flags. Here is an example. Recall that in lab 2 we have the problem of counting the occurrence of digits in user inputs. We used an array of 10 integers where each integer element is a counter. Now consider a simplified version of the problem: you don't need to count the number of occurrences of each digit, instead we just need to record whether each digit has appeared in the input or not (no matter how many times they appear). For example, for input BECS20310N, 2019-21EW, LAS0006, we need to record that 0,1,2,3, 6 and 9 do appear in the inputs, but 4,5,7 and 8 don't. One way to do this is to maintain an array of 10 (short) integers, where each integer element is used as a Boolean flag: O for False (absent) and 1 for True (present). Now imagine in old days when memory is very limited, and thus instead of 10 integers, which takes 80-320 bits, you can only afford to use one integer (16-32 bits) to do the job. Is it possible? Here the bitwise operations come to the rescue. The idea is that since we only need a True/False info for each digit, 1 bit is enough for each digit, so we need only a total of 10 bits to record. Thus an integer or even a short integer is enough. Specifically, we declare a short int variable named flags, which usually has 16 bits. Then we designate 10 bits in flags as Boolean flags digits 0~9. For example, we designate the right most bit (denoted bit-o) as the Boolean flag for digit 0, designate the next bit (denoted bit-1) as the Boolean flag for digits 1, and so on. flags is initially set to 0. Then after reading the first digit, say, 2, we use bitwise operation to turn on" (set to 1) bit-2 of flags. So flags' bit representation becomes 0000000000000100. Later when reading another 2, you can somehow check if bit-2 is on and turns it on if not, or alternatively, simply use the same operation to turn on bit-2 of flags, although bit-2 is already on. After reading all inputs EECS20310N, EW2019-21, LAS1006A, which contains digit 0,1,2,3,6 and 9, the internal representation of flags becomes 0000010 01001111. That is, bit 0,1,2,3,6 and 9 are on. Finally, we can use bitwise operations to examine the lower 10 bits of flags, determining which are 1 and which are 0. Implementation Download partially implemented file lab3flags.c. Similar to lab2c.c, this program keeps on reading inputs using getchar until end of file is entered. It then outputs if each digits is present in the inputs or not. Observe that by putting getchar in the loop header, we just need to call getchar once. (But a parenthesis is needed due to operator precedence). Complete the loop body, using one of the idioms mentioned on previous page, so that flags is updated properly after reading a digit char. Complete the output part, by checking the right most 9 bits one by one. Hint: there are at least two approaches to check whether a particular bit is 1 or 0. One of the idiom mention earlier can do this, another approach is hinted in the printBinary function provided. For your convenience, a function printBinary() is defined and used to output the binary representation of flags, both before and after user inputs. It is interesting to observe that function printBinary() itself uses bitwise operations to generate artificial 'O' or '1', printing the binary representation of an int. It would be interesting to trace the code. This may help you complete the output part. Sample inputs/outputs (download input2.txt from lab2) red 369 % a.out flags : 0000000000000000 YorkU LAS C AD (press Ctrl and D) flags: 00000000 00000000 0: no 1: no 2: no 3: no 4: no 5: no 6: no 7: no 8: no 9: no red 370 % a.out flags : 00000000 00000000 EECS20310N FW2019-21 LAS1006A *D (press Ctrl and D) flags: 00000010 01001111 0: yes 1: yes 2: yes 3: yes 4: no 5: no 6: yes 7: no 8: no 9: yes red 371 % a.out flags: 00000000 00000000 EECS3421 this is good 3 address 500 yu264067 429Dk *D (press Ctrl and D) flags : 00000010 11111111 0: yes 1: yes 2: yes 3: yes 4: yes 5: yes 6: yes 7: yes 8: no 9: yes red 372 * a.out #define SIZE 16 void printBinary(short int); /*counting digits*/ int main() { int c, i, index; short flags = 0; printf("flags:"); printBinary(flags); printf(" "); while ((c = getchar()) != EOF) { if ( ){ // if c is a digit with numerical value x, turn bit x of flags on } } printf(" flags:"); printBinary(flags); printf(" "); // output by checking the lower 10 bits one by one // hint: at least two apporches for this. // you can use one idiom mentioned in lab manual, or get hint 11 from the printBinary() function below. for(i=0; i>= 1; COU--; } int i=0; for(; i