spring pendulum (answer question b-e with explanation please)

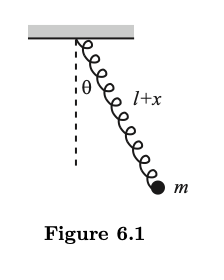
mass "m" is connected to a fixed point O by a rigid massless spring of force "k" and initial length "l". it executes a pendulum motion in a vertical plane under gravity "g"

a) using generalized coordinates to find Lagrangian and Euler-Lagrange equations

b) find all equilibrium positions? are they stable or not?

c) find small oscillation frequencies at the stable equilibrium position -- 2 distinct frequencies for the two degrees of freedom

d) find the tension in the spring by the Lagrange multiplier

e) write the conjugate momenta, and also write the Hamiltonian and the conjugate momenta.

D I+x Figure 6.1Solution: The kinetic energy may be broken up into the radial and tangential parts, so we have T = -m(2 + (1+2) 202) (6.9) The potential energy comes from both gravity and the spring, so we have V(x, 0) = -mg(l + x) cos0 + - kx2. (6.10) The Lagrangian is therefore LET - V =,m(x2 + ((+x)202 ) +mg(+ x) cos0 - -kx2. (6.11) 6.1. THE EULER-LAGRANGE EQUATIONS VI-3 There are two variables here, > and 0. As mentioned above, the nice thing about the La- grangian method is that we can just use eq. (6.3) twice, once with a and once with 0. So the two Euler-Lagrange equations are d ( OL OL dt di ax mi = m(l + x)02 + mgcos0 - kx, (6.12) and d ( OL OL at (m(l + x)20) = -mg(l + x) sine m(l + x)20 +2m(l+ x)ice = -mg(l + x) sine. m(l + x)0 + 2mi0 = -mgsine. (6.13)