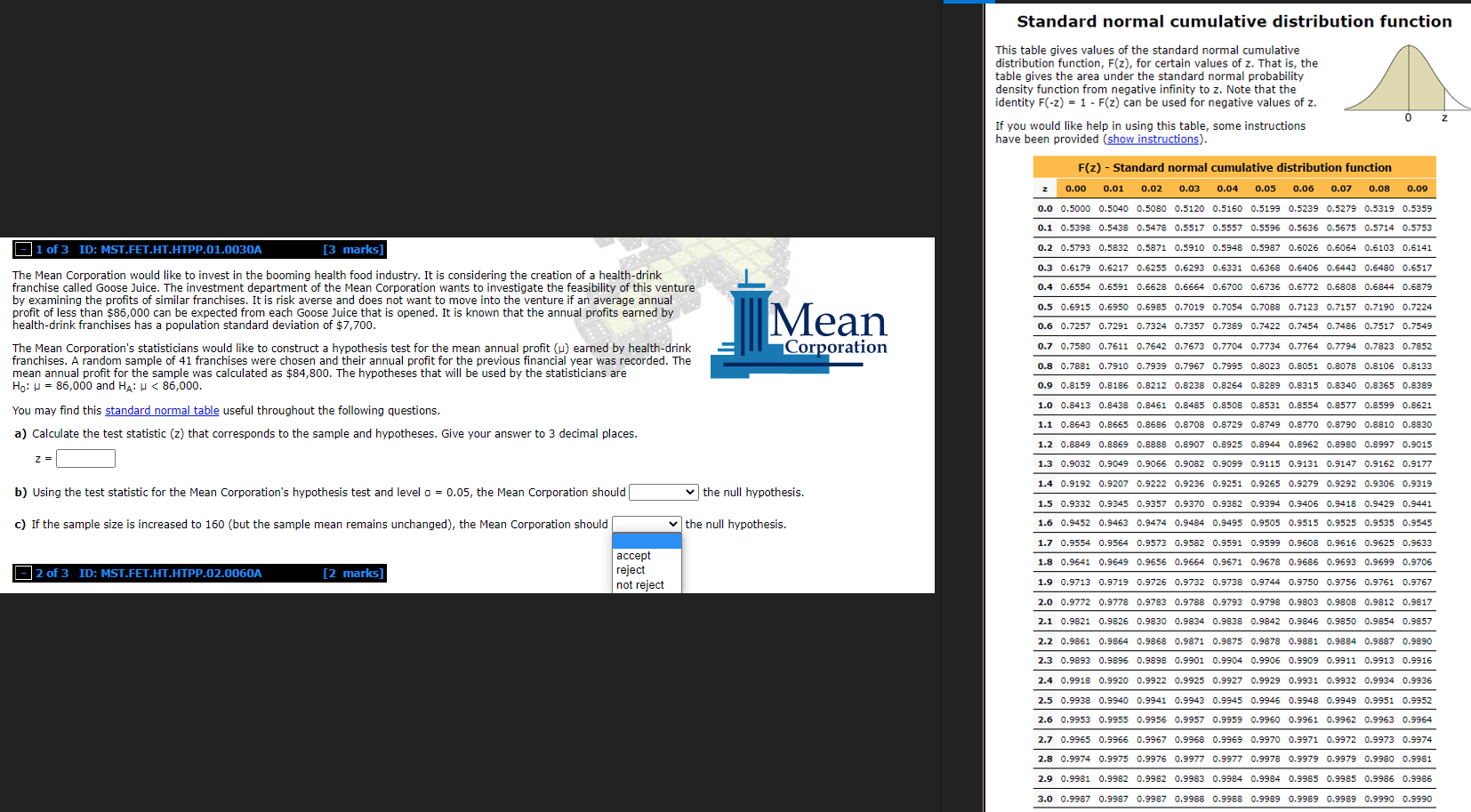
Standard normal cumulative distribution function This table gives values of the standard normal cumulative distribution function, F(z), for certain values of z. That is, the table gives the area under the standard normal probability density function from negative infinity to z. Note that the identity F(-z) = 1 - F(z) can be used for negative values of z. If you would like help in using this table, some instructions have been provided (show instructions) F(z) - Standard normal cumulative distribution function 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.5398 0.5438 0.5478 0.5517 0.5557 0 0.5596 0.5636 0.5675 0.5714 0.5753 1 of 3 ID: MST.FET.HT.HTPP.01.0030A [3 marks] 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 The Mean Corporation would like to invest in the booming health food industry. It is considering the creation of a health-drink franchise called Goose Juice. The investment department of the Mean Corporation wants to investigate the feasibility of this venture 0.4 0. 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0 0.6879 by examining the profits of similar franchises. It is risk averse and does not want to move into the venture if an average annual profit of less than $86,000 can be expected from each Goose Juice that is opened. It is known that the annual profits earned by Mean 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 health-drink franchises has a population standard deviation of $7,700. 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 The Mean Corporation's statisticians would like to construct a hypothesis test for the mean annual profit () earned by health-drink Corporation 0.7580 0. 0.7611 0.7642 0.7673 0.7704 0 4 0.7734 0.7764 0.7794 0.7823 0.7852 franchises. A random sample of 41 franchises were chosen and their annual profit for the previous financial year was recorded. The 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 mean annual profit for the sample was calculated as $84,800. The hypotheses that will be used by the statisticians are Ho: H = 86,000 and HA: U