stat and prob:-
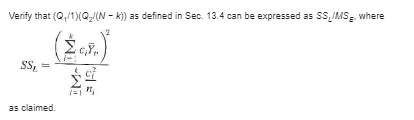
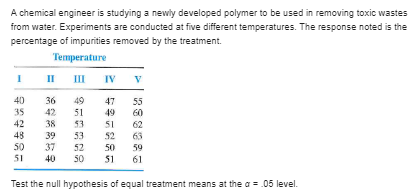
Verify that (Q,/1)(Q,/(N - k)) as defined in Sec. 13.4 can be expressed as SS IMS where SS, = E as claimed.Let Y , Yo., You and Yo denote the sample means based on independent samples drawn from normal distributions with means p. . P2. P;. and py. respectively. Find the contrast sum of squares for each of the contrasts of Exercise 24, parts (8). (e). and (f).Consider the orthogonal contrasts of Exercise 24(e). Use the data of Exercise 22 to find the numerical values of Mis, and DY . Since k= 4, there exists a third contrast that is orthogonal to L, and Ly. What is the numerical value of SS,, ?A chemical engineer is studying a newly developed polymer to be used in removing toxic wastes from water. Experiments are conducted at five different temperatures. The response noted is the percentage of impurities removed by the treatment. Temperature II ITI IV 40 36 49 47 in 35 42 51 42 51 49 39 53 50 37 52 50 $1 40 50 $1 61 Test the null hypothesis of equal treatment means at the a = .05 level.A chemical engineer is studying a newly developed polymer to be used in removing toxic wastes from water. Experiments are conducted at five different temperatures. The response noted is the percentage of impurities removed by the treatment. Temperature II III IV 40 36 49 47 55 35 43 51 49 60 42 51 62 49 39 53 50 37 52 507 50 $1 40 50 $1 61 Use Bonferroni Ttests with a's 25 to compare all possible pairs of means. Report your results schematically by ordering the sample means from the smallest to the largest and underlining pairs that are not significantly different.A chemical engineer is studying a newly developed polymer to be used in removing toxic wastes from water. Experiments are conducted at five different temperatures. The response noted is the percentage of impurities removed by the treatment. Temperature II ITI IV 40 30 49 47 55 42 51 44 60 42 51 62 70 50 50 50 40 50 61 Write a contrast that can be used to compare the mean of population 5 to the aggregate of the other four means. Test the null hypothesis that this contrast assumes the value 0. Interpret your results in the context of this exercise.A quality control engineer conducted an experiment to investigate the effect of experience on an assembly line in terms of the average time required to complete an assembly task. If experience is found to be a factor, a training program is planned for newer employees. The engineer randomly selected eight employees from groups who had completed 1, 2, 3, and 4 years of work experience, respectively. He set up the experiment as a randomized block design with tasks as blocks and years of experience as treatments. The resulting data are given below. Time to complete assembly tasks Experience Task 1 year 2 years 3 years 4 years 40,3 34.2 28.8 26.6 25.4 25.4 29.2 21.2 28 2 28.0 24.6 23.2 41.6 24.9 29.1 27.0 23.8 39.2 34.8 27.1 38. 29.5 26.6 27.3 20.4 29.0 36.0 34.2 37.7 25.6 25.6 25.2 Write the appropriate statistical model for this experiment.A quality control engineer conducted an experiment to investigate the effect of experience on an assembly line in terms of the average time required to complete an assembly task. If experience is found to be a factor, a training program is planned for newer employees. The engineer randomly selected eight employees from groups who had completed 1, 2, 3, and 4 years of work experience, respectively. He set up the experiment as a randomized block design with tasks as blocks and years of experience as treatments. The resulting data are given below. Time to complete assembly tasks Experience Task 1 year 2 years 3 years 4 years 40,3 34.2 28.8 26.6 25.4 25.4 29.2 21.2 28. 2 280 24.6 23.2 41.6 249 29.1 27.0 23. 39.2 34.8 27.1 38.7 29 5 26.6 27.3 29.4 29.0 36.0 34.2 37.7 25.6 25.6 25.2 Test for any significant differences among years of experience for average assembly time. Use a = .05.A quality control engineer conducted an experiment to investigate the effect of experience on an assembly line in terms of the average time required to complete an assembly task. If experience is found to be a factor, a training program is planned for newer employees. The engineer randomly selected eight employees from groups who had completed 1, 2, 3, and 4 years of work experience, respectively. He set up the experiment as a randomized block design with tasks as blocks and years of experience as treatments. The resulting data are given below. Time to complete assembly tasks Experience Task 1 year 2 years 3 years 4 years 40,3 34.2 28.8 26.6 254 25.4 29.2 21.2 28.0 24.6 23.2 41.6 249 29.1 27.0 3.8 30 34.8 27.1 3 29 5 26.6 27.3 20.4 29.0 36.0 34.2 37.7 25.6 25.6 25.2 Was blocking appropriate? Explain.A quality control engineer conducted an experiment to investigate the effect of experience on an assembly line in terms of the average time required to complete an assembly task. If experience is found to be a factor, a training program is planned for newer employees. The engineer randomly selected eight employees from groups who had completed 1, 2, 3, and 4 years of work experience, respectively. He set up the experiment as a randomized block design with tasks as blocks and years of experience as treatments. The resulting data are given below. Time to complete assembly tusks Experience Task 1 year 1 years 3 years 4 years 40,3 34.2 28.8 26.6 25.4 25.4 29.2 21.2 28.2 28.0 24.6 23.2 41.6 24.9 29.1 27.0 28.8 39.2 34.8 27.1 38.7 29.5 26.6 27.3 20.4 20.0 36.0 34.2 37.7 25.6 25.6 25.2 How many paired comparisons are possible? If these comparisons are made by means of Bonferroni paired 7 tests, what o level must be used to attain an overall level of significance that is at most . 10?A quality control engineer conducted an experiment to investigate the effect of experience on an assembly line in terms of the average time required to complete an assembly task. If experience is found to be a factor, a training program is planned for newer employees. The engineer randomly selected eight employees from groups who had completed 1, 2, 3, and 4 years of work experience, respectively. He set up the experiment as a randomized block design with tasks as blocks and years of experience as treatments. The resulting data are given below. Time to complete assembly tusks Experience Task 1 year 2 years 3 years 4 years 40.3 34.2 28.8 26.6 25.4 25.4 29.2 21.2 28.2 28.0 24.6 23.2 41.6 249 29.1 27.0 23.8 39.2 34.8 27.1 38.7 29.5 26.6 27.3 29.4 29.0 36.0 34.2 37.7 25.6 25.6 25.2 Use Bonferroni 7 tests to determine which treatments (number of years of experience), if any, differ significantly with o' s .10.A quality control engineer conducted an experiment to investigate the effect of experience on an assembly line in terms of the average time required to complete an assembly task. If experience is found to be a factor, a training program is planned for newer employees. The engineer randomly selected eight employees from groups who had completed 1, 2, 3, and 4 years of work experience, respectively. He set up the experiment as a randomized block design with tasks as blocks and years of experience as treatments. The resulting data are given below. Time to complete assembly tasks Experience Task 1 year 1 years 3 years 4 years 40,3 34.2 28.8 26.6 25.4 25.4 29.2 21.2 28.2 28.0 24.6 23.2 41.6 249 29.1 27.0 23.8 39.2 34.8 27.1 38.7 29 26.6 27.3 29.4 29.0 36.0 34.2 37.7 25.6 25.6 25.2 Do the data suggest that a training program might be productive?A computer scientist is studying four different algorithms used to perform numerical integration. The speed (in seconds) with which a problem can be solved is measured. Each algorithm is to be used to solve each of 10 different problems, and hence a problem serves as a block. Algorithm Problem II III IV 10 .11 .16 .10 .11 .13 .17 .09 13 .14 .17 . 12 08 .11 .13 .09 .16 .19 .16 BOX JOHAWN- . 18 23 .16 .07 .11 .07 . 15 .18 14 12 .14 .15 . 12 10 .16 .15 .20 15 Test for differences among the mean times required to solve integration problems for these algorithms.A computer scientist is studying four different algorithms used to perform numerical integration. The speed (in seconds) with which a problem can be solved is measured. Each algorithm is to be used to solve each of 10 different problems, and hence a problem serves as a block. Algorithm Problem II III IV 10 .16 .10 .11 13 .17 .09 13 .14 .17 . 12 .11 .13 09 .16 .19 BOX JAVAWN- 18 .16 .07 11 .07 .13 .15 .18 .14 .12 .14 .15 .12 16 .15 .20 .15 Estimate the relative efficiency, and use it to discuss the desirability of blocking in a future study of this sort