Statistics

Rules

Please answer as much as possible for like!

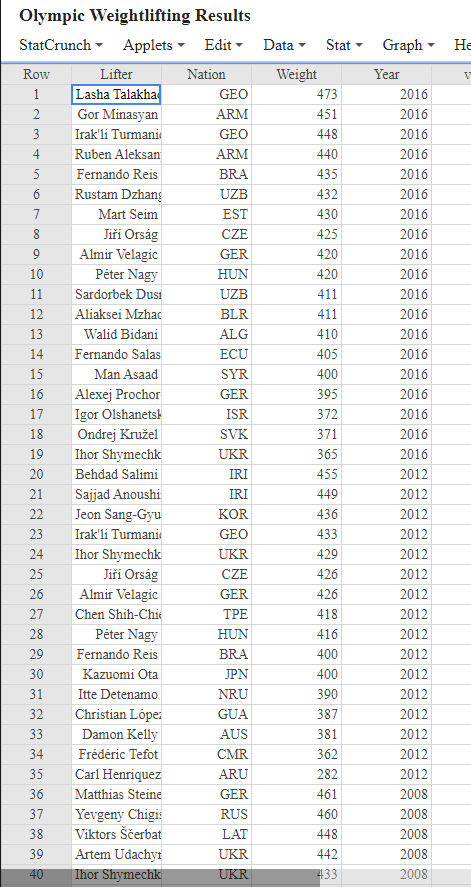
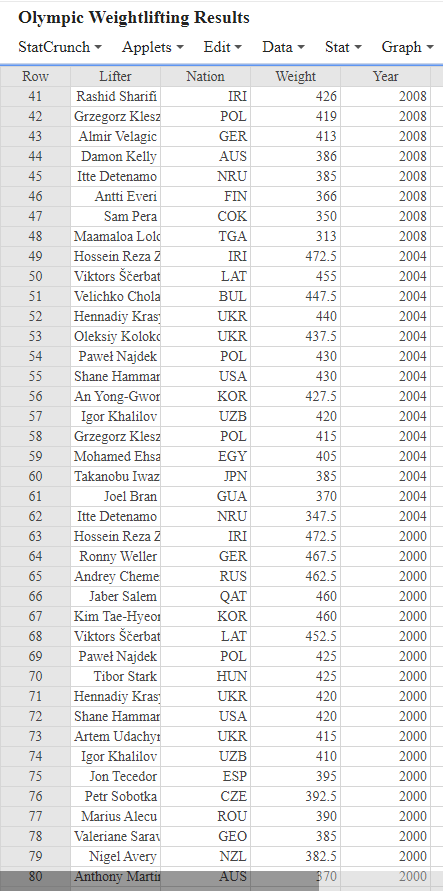
Use complete and coherent sentences to answer the questions. Graphs must be appropriately titled and should refer to the context of the question. Graphical displays must include labels with units if appropriate for each axis. Units should always be included when referring to numerical values. When making a comparison you must use comparative language, such as greater than, less than", or "about the same as. Ensure that all graphs and tables appear on one page and are not split across two pages. Type all mathematical calculations when directed to compute an answer by-hand.' Pictures of actual handwritten work are not accepted on this assignment. When writing mathematical expressions into your solutions document you may use either an equation editor or common shortcuts. For example, V can be written as sqrt(x), p can be written as p-hat, and i can be written as x-bar. V 5 000 411 400 Olympic Weightlifting Results StatCrunch Applets Edit Data Stat Graph - He Row Lifter Nation Weight Year 1 Lasha Talakha GEO 473 2016 2 Gor Minasyan ARM 451 2016 3 Irak'li Turmani GEO 448 2016 4 Ruben Aleksan ARM 440 2016 5 Fernando Reis BRA 435 2016 6 Rustam Dzhang UZB 432 2016 7 Mart Seim EST 430 2016 8 Ji Orsg CZE 425 2016 Almir Velagic GER 420 2016 10 Pter Nagy HUN 420 2016 11 Sardorbek Dusi UZB 411 2016 12 Aliaksei Mzhac BLR 2016 13 Walid Bidani ALG 410 2016 14 Fernando Salas ECU 405 2016 15 Man Asaad SYR 2016 16 Alexej Prochor GER 395 2016 17 Igor Olshanets! ISR 372 2016 18 Ondrej Kruel SVK 371 2016 19 Thor Shymechk UKR 365 2016 20 Behdad Salimi IRI 455 2012 21 Sajjad Anoushi IRI 449 2012 22 Jeon Sang-Gyu KOR 436 2012 23 Irak'li Turmani GEO 433 2012 24 Ihor Shymechk UKR 429 2012 25 Ji Orsg CZE 426 2012 26 Almir Velagic GER 426 2012 27 Chen Shih-Chic TPE 418 2012 28 Pter Nagy HUN 416 2012 29 Fernando Reis BRA 400 2012 30 Kazuomi Ota 400 2012 31 Itte Detenamo NRU 390 2012 32 Christian Lpe: GUA 387 2012 33 Damon Kelly AUS 381 2012 34 Frdric Tefot CMR 362 2012 35 Carl Henriquez ARU 282 2012 36 Matthias Steine GER 2008 37 Yevgeny Chigi: RUS 460 2008 38 Viktors erbat LAT 448 2008 39 Artem Udachyt UKR 442 2008 40 Thor Shymechk UKR 433 2008 JPN 461 FIN Olympic Weightlifting Results StatCrunch Applets Edit Data Stat Row Lifter Nation Weight 41 Rashid Sharifi IRI 426 42 Grzegorz Klesz POL 419 43 Almir Velagic GER 413 44 Damon Kelly AUS 386 45 Itte Detenamo NRU 385 46 Antti Everi 366 47 Sam Pera COK 350 48 Maamaloa Lold TGA 313 49 Hossein Reza z IRI 472.5 50 Viktors erbat LAT 455 51 Velichko Chola BUL 447.5 52 Hennadiy Kras UKR 440 53 Oleksiy Kolok UKR 437.5 54 Pawe Najdek POL 430 55 Shane Hammar USA 430 56 An Yong-Gwor KOR 427.5 57 Igor Khalilov UZB 420 58 Grzegorz Klesz POL 415 59 Mohamed Ehsa EGY 405 60 Takanobu Iwaz JPN 385 61 Joel Bran GUA 370 62 Itte Detenamo NRU 347.5 63 Hossein Reza 2 IRI 472.5 64 Ronny Weller GER 467.5 65 Andrey Cheme RUS 462.5 66 Jaber Salem QAT 460 67 Kim Tae-Hyeol KOR 460 68 Viktors erbat LAT 452.5 Pawe Najdek POL 425 70 Tibor Stark HUN 425 71 Hennadiy Kras UKR 420 72 Shane Hammar USA 420 73 Artem Udachyt UKR 415 74 Igor Khalilov UZB 410 75 Jon Tecedor ESP 395 76 Petr Sobotka CZE 392.5 77 Marius Alecu ROU 390 78 Valeriane Saray GEO 385 79 Nigel Avery NZL 382.5 80 Anthony Marti AUS 370 Graph Year 2008 2008 2008 2008 2008 2008 2008 2008 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 81 82 83 Chris Rae Alesana Sione Playter Reyes AUS ASA DOM 360 357.5 352.5 2000 2000 2000 Investigation 4: Super-Heavyweight Weightlifting Grouped by Year We will continue to analyze data collected from the Men's Super-Heavyweight Weightlifting Olympic Event between the years 2000-2016. . Data in StatCrunch titled "Olympic Weightlifting Results present the participant's name, nation, final weight lift (in kilograms) (this variable is called Weight Lifted), and the year it occurred (source: olmpedia.org). a) Construct a boxplot for the Final Weight Lift variable grouped by the "Year variable (select Year under Group by:). Properly title and label your graph. Copy and paste this graph into your solutions document. b) Obtain the samples size, mean, median, standard deviation, IQR, and maximum in StatCrunch of the Final Weight Lift variable grouped by the Year variable. Please keep the listed statistics in the order presented above when you present your statistics in a table. Copy and paste the table you obtain into your solutions document. Round all statistics to one decimal place when necessary. c) Discuss one interesting discovery you made about this data set using the graph and numerical summaries presented in parts (a) and (b). d) Which two years would you define as the most symmetric? Use a comparison of the mean and median to help you answer this question in one sentence. e) Using the IQR values from part (b), compare the variation or spread of the weights lifted from the years 2000 and 2016 by IQR. Answer this part in one sentence. b For parts 4(f) - 4(i), determine how well the Empirical Rule does in predicting the percentage of observations within some number of standard deviations of the mean. f) Use your rounded summary statistics for 2016" from part 4(b) to calculate the interval corresponding to one, two, and three standard deviations about the mean of the Final Weight Lift. Type your work showing how you obtained these intervals. Clearly label and list these three intervals in your solutions document as shown below: 68% interval (lower value, upper value) 95% interval (lower value, upper value) 99.7% interval (lower value, upper value) g) Use StatCrunch to determine the frequency AND percentage of observations falling in each of these intervals by following the instructions listed below or using another appropriate counting method. Properly label and list these counts and percentages in your solutions document. Go to Data Row Selection Interactive Tools. In the Slider selectors box, click the variable "Final Weight Lift into the variable box. In the Category selectors box, click the variable "Year" into the variable box. Click "Compute!" to open the tool. The box that appears has a slider under the words Final Weight Lift that allows you to create ranges of scores that you determined in 4(f). Under Year, select the Year 2016. Use the slider to obtain the count for each interval from 4(f) by looking at the # rows selected" presented in the first line of the box. Hint: click on the square bounds of the interval and use your arrow keys for more control. Calculate the percentages from the counts you obtained for each interval and include them in your solutions document. h) Do each of the three percentages found in part 4(g) match what the Empirical Rule predicts? Compare your results in 4(g) with the expected percentage stated in the Empirical Rule. State your answer in three sentences (one sentence for each comparison). i) Suppose in the next Olympics, a random weightlifter lifted 490 kg. Use your rounded summary statistics from the year 2016, calculate the z-score of this value and explain in a complete sentence what this z-score indicates. Round the z-score to two decimal places. Use complete and coherent sentences to answer the questions. Graphs must be appropriately titled and should refer to the context of the question. Graphical displays must include labels with units if appropriate for each axis. Units should always be included when referring to numerical values. When making a comparison you must use comparative language, such as greater than, less than", or "about the same as. Ensure that all graphs and tables appear on one page and are not split across two pages. Type all mathematical calculations when directed to compute an answer by-hand.' Pictures of actual handwritten work are not accepted on this assignment. When writing mathematical expressions into your solutions document you may use either an equation editor or common shortcuts. For example, V can be written as sqrt(x), p can be written as p-hat, and i can be written as x-bar. V 5 000 411 400 Olympic Weightlifting Results StatCrunch Applets Edit Data Stat Graph - He Row Lifter Nation Weight Year 1 Lasha Talakha GEO 473 2016 2 Gor Minasyan ARM 451 2016 3 Irak'li Turmani GEO 448 2016 4 Ruben Aleksan ARM 440 2016 5 Fernando Reis BRA 435 2016 6 Rustam Dzhang UZB 432 2016 7 Mart Seim EST 430 2016 8 Ji Orsg CZE 425 2016 Almir Velagic GER 420 2016 10 Pter Nagy HUN 420 2016 11 Sardorbek Dusi UZB 411 2016 12 Aliaksei Mzhac BLR 2016 13 Walid Bidani ALG 410 2016 14 Fernando Salas ECU 405 2016 15 Man Asaad SYR 2016 16 Alexej Prochor GER 395 2016 17 Igor Olshanets! ISR 372 2016 18 Ondrej Kruel SVK 371 2016 19 Thor Shymechk UKR 365 2016 20 Behdad Salimi IRI 455 2012 21 Sajjad Anoushi IRI 449 2012 22 Jeon Sang-Gyu KOR 436 2012 23 Irak'li Turmani GEO 433 2012 24 Ihor Shymechk UKR 429 2012 25 Ji Orsg CZE 426 2012 26 Almir Velagic GER 426 2012 27 Chen Shih-Chic TPE 418 2012 28 Pter Nagy HUN 416 2012 29 Fernando Reis BRA 400 2012 30 Kazuomi Ota 400 2012 31 Itte Detenamo NRU 390 2012 32 Christian Lpe: GUA 387 2012 33 Damon Kelly AUS 381 2012 34 Frdric Tefot CMR 362 2012 35 Carl Henriquez ARU 282 2012 36 Matthias Steine GER 2008 37 Yevgeny Chigi: RUS 460 2008 38 Viktors erbat LAT 448 2008 39 Artem Udachyt UKR 442 2008 40 Thor Shymechk UKR 433 2008 JPN 461 FIN Olympic Weightlifting Results StatCrunch Applets Edit Data Stat Row Lifter Nation Weight 41 Rashid Sharifi IRI 426 42 Grzegorz Klesz POL 419 43 Almir Velagic GER 413 44 Damon Kelly AUS 386 45 Itte Detenamo NRU 385 46 Antti Everi 366 47 Sam Pera COK 350 48 Maamaloa Lold TGA 313 49 Hossein Reza z IRI 472.5 50 Viktors erbat LAT 455 51 Velichko Chola BUL 447.5 52 Hennadiy Kras UKR 440 53 Oleksiy Kolok UKR 437.5 54 Pawe Najdek POL 430 55 Shane Hammar USA 430 56 An Yong-Gwor KOR 427.5 57 Igor Khalilov UZB 420 58 Grzegorz Klesz POL 415 59 Mohamed Ehsa EGY 405 60 Takanobu Iwaz JPN 385 61 Joel Bran GUA 370 62 Itte Detenamo NRU 347.5 63 Hossein Reza 2 IRI 472.5 64 Ronny Weller GER 467.5 65 Andrey Cheme RUS 462.5 66 Jaber Salem QAT 460 67 Kim Tae-Hyeol KOR 460 68 Viktors erbat LAT 452.5 Pawe Najdek POL 425 70 Tibor Stark HUN 425 71 Hennadiy Kras UKR 420 72 Shane Hammar USA 420 73 Artem Udachyt UKR 415 74 Igor Khalilov UZB 410 75 Jon Tecedor ESP 395 76 Petr Sobotka CZE 392.5 77 Marius Alecu ROU 390 78 Valeriane Saray GEO 385 79 Nigel Avery NZL 382.5 80 Anthony Marti AUS 370 Graph Year 2008 2008 2008 2008 2008 2008 2008 2008 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2004 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 81 82 83 Chris Rae Alesana Sione Playter Reyes AUS ASA DOM 360 357.5 352.5 2000 2000 2000 Investigation 4: Super-Heavyweight Weightlifting Grouped by Year We will continue to analyze data collected from the Men's Super-Heavyweight Weightlifting Olympic Event between the years 2000-2016. . Data in StatCrunch titled "Olympic Weightlifting Results present the participant's name, nation, final weight lift (in kilograms) (this variable is called Weight Lifted), and the year it occurred (source: olmpedia.org). a) Construct a boxplot for the Final Weight Lift variable grouped by the "Year variable (select Year under Group by:). Properly title and label your graph. Copy and paste this graph into your solutions document. b) Obtain the samples size, mean, median, standard deviation, IQR, and maximum in StatCrunch of the Final Weight Lift variable grouped by the Year variable. Please keep the listed statistics in the order presented above when you present your statistics in a table. Copy and paste the table you obtain into your solutions document. Round all statistics to one decimal place when necessary. c) Discuss one interesting discovery you made about this data set using the graph and numerical summaries presented in parts (a) and (b). d) Which two years would you define as the most symmetric? Use a comparison of the mean and median to help you answer this question in one sentence. e) Using the IQR values from part (b), compare the variation or spread of the weights lifted from the years 2000 and 2016 by IQR. Answer this part in one sentence. b For parts 4(f) - 4(i), determine how well the Empirical Rule does in predicting the percentage of observations within some number of standard deviations of the mean. f) Use your rounded summary statistics for 2016" from part 4(b) to calculate the interval corresponding to one, two, and three standard deviations about the mean of the Final Weight Lift. Type your work showing how you obtained these intervals. Clearly label and list these three intervals in your solutions document as shown below: 68% interval (lower value, upper value) 95% interval (lower value, upper value) 99.7% interval (lower value, upper value) g) Use StatCrunch to determine the frequency AND percentage of observations falling in each of these intervals by following the instructions listed below or using another appropriate counting method. Properly label and list these counts and percentages in your solutions document. Go to Data Row Selection Interactive Tools. In the Slider selectors box, click the variable "Final Weight Lift into the variable box. In the Category selectors box, click the variable "Year" into the variable box. Click "Compute!" to open the tool. The box that appears has a slider under the words Final Weight Lift that allows you to create ranges of scores that you determined in 4(f). Under Year, select the Year 2016. Use the slider to obtain the count for each interval from 4(f) by looking at the # rows selected" presented in the first line of the box. Hint: click on the square bounds of the interval and use your arrow keys for more control. Calculate the percentages from the counts you obtained for each interval and include them in your solutions document. h) Do each of the three percentages found in part 4(g) match what the Empirical Rule predicts? Compare your results in 4(g) with the expected percentage stated in the Empirical Rule. State your answer in three sentences (one sentence for each comparison). i) Suppose in the next Olympics, a random weightlifter lifted 490 kg. Use your rounded summary statistics from the year 2016, calculate the z-score of this value and explain in a complete sentence what this z-score indicates. Round the z-score to two decimal places