Step 4Step 2To determine the critical numbers of g(x), set g'(x) equal to zero and solve for x.g'(x) = 0g(x).g(x) = x - 6x -

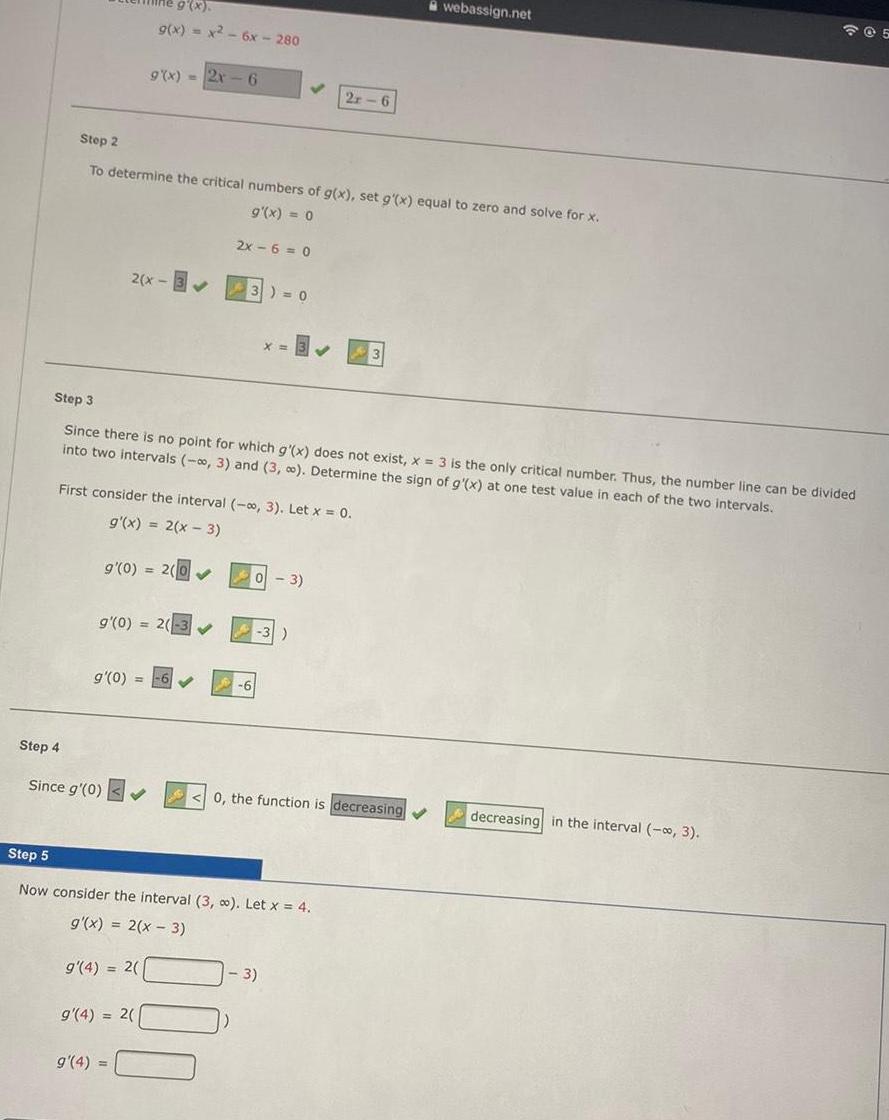
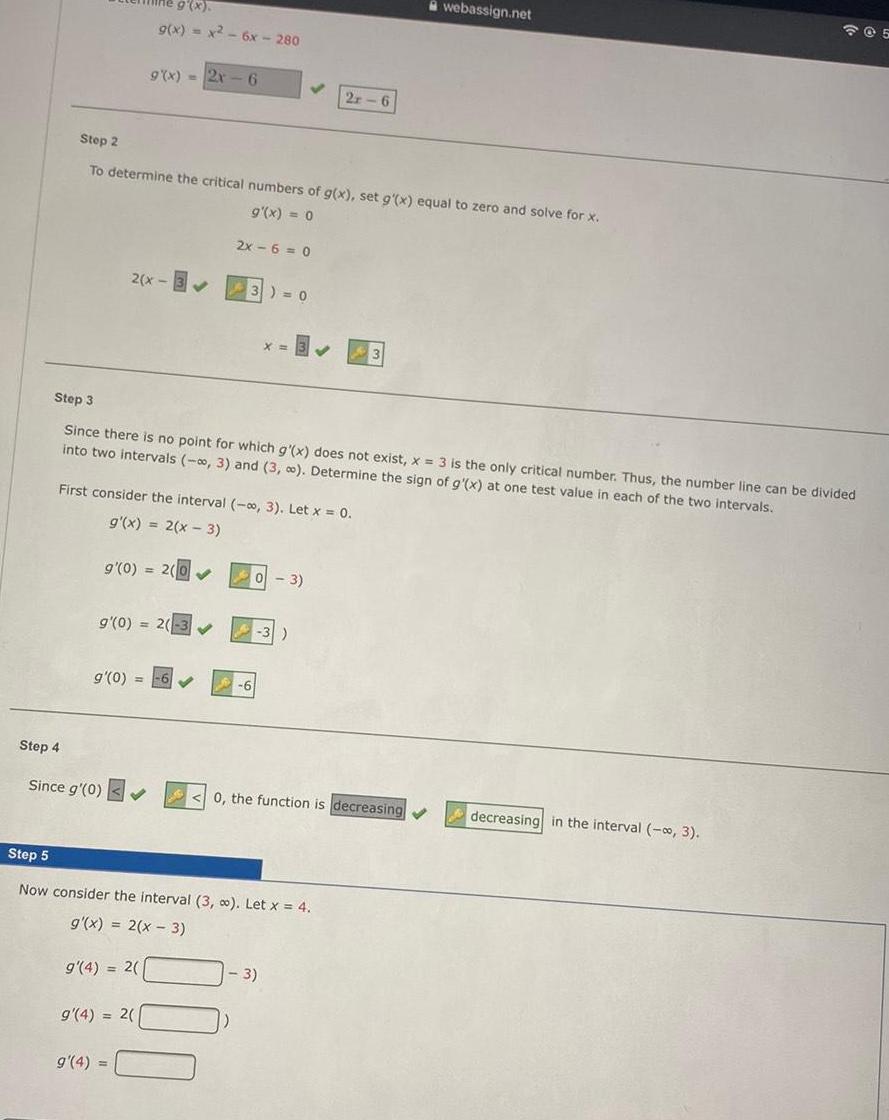
Step 4Step 2To determine the critical numbers of g(x), set g'(x) equal to zero and solve for x.g'(x) = 0g(x).g(x) = x² - 6x - 2802(x-33) = 0g'(0) =9(x)=2x-6g'(0) = 2(-3?Since g'(0) ?First consider the interval (-?, 3). Let x = 0.g'(x) = 2(x-3)9'(0) = 2(0?Step 3Since there is no point for which g'(x) does not exist, x = 3 is the only critical number. Thus, the number line can be dividedinto two intervals (-?, 3) and (3, ?). Determine the sign of g'(x) at one test value in each of the two intervals.g'(4) = 2(g'(4) = 2(g'(4) =2x-6=0?X=Step 5Now consider the interval (3, ?). Let x = 4.g'(x) = 2(x - 3)2r-6- 3)-3)- 3)0, the function is decreasing ?webassign.net205decreasing in the interval (-?, 3).